AVL 트리
균형 이진탐색트리.
정의
루트노드 R의 왼쪽. 오른쪽 서브트리 높이 차가 1 이내인 ‘이진탐색트리’.
- 언제나 높이 균형이 유지된다.
특징
높은 시간 효율성.
$\Rightarrow$ 항상 $O(\log_{2}{n})$ 시간복잡도 보장.
- 따라서 $O(n)$ 시간복잡도(최악경우) 걸릴 일 없다.
예시

회전연산
균형유지 연산.
정의
AVL 트리에 데이터 삽입. 삭제 후 균형 맞추기 위해 ‘서브트리가 회전’하는 연산.
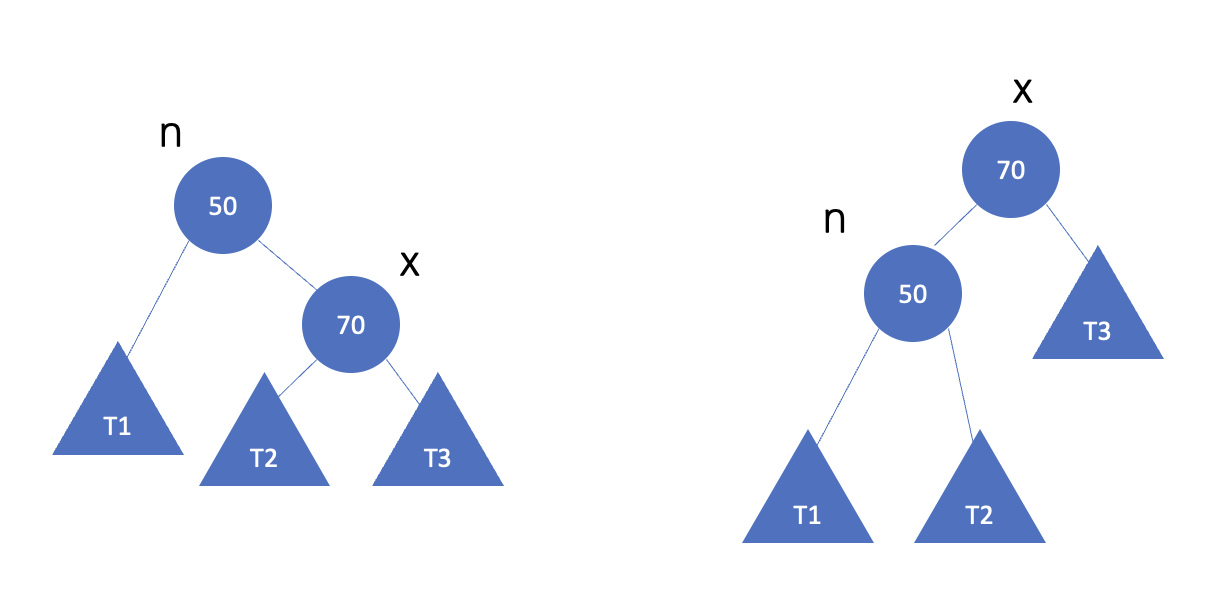
기반
rotate_right()
AVL트리에서 루트 왼쪽 서브트리가 오른쪽 보다 더 높아 불균형 발생할 경우.
서브트리가 오른쪽으로 회전.

rotate_left()
AVL트리에서 루트 오른쪽 서브트리가 왼쪽 보다 더 높아 불균형 발생할 경우.
서브트리가 왼쪽으로 회전.
아래는 rotate_right(), roate_left()를 기반으로 한.
각 상황 별 회전연산이다.
‘상황 - 회전’
LL- 회전
rotate_right() 사용
조건
(루트 왼쪽 서브트리 높이 $-$ 오른쪽 서브트리 높이) $> 1$
$+$ 그 왼쪽 서브트리 안에서 $>$ (왼쪽 서브트리 높이 $-$ 오른쪽 서브트리 높이) $> 0$

RR - 회전
rotate_left() 사용
조건
(루트 왼쪽 서브트리 높이 $-$ 오른쪽 서브트리 높이) $< -1$
$+$ 그 오른쪽 서브트리 안에서 $>$ (왼쪽 서브트리 높이 $-$ 오른쪽 서브트리 높이) $< 0$

LR - 회전
1. 루트 왼쪽 서브트리에서 rotate_left()
2. 루트에서 rotate_right()
조건
(루트 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이) $> 1$
$+$ 그 왼쪽 서브트리 안에서 $>$ (왼쪽 서브트리 높이 - 오른쪽 서브트리 높이) $< 0$

RL - 회전
1. 루트 오른쪽 서브트리에서 rotate_right()
2. 루트에서 rotate_left()
조건
(루트 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이) $< -1$
$+$ 그 오른쪽 서브트리 안에서 $>$ (왼쪽 서브트리 높이 - 오른쪽 서브트리 높이) $> 0$

LL, RR, RL, LR 회전연산 공통점
- 시간복잡도 모두 $O(1)$: 변경된 노드 레퍼런스 수가 $O(1)$ 개 이기 때문이다.
- 회전 후 트리 형상. 모두 동일하다.
4종류 회전연산 정의
- 트리에서는 항상 연산 후 루트R 반환한다.
LL - 회전
1
2
3
4
5
6
7
8
# LL - 회전 정의
## LL
def rotate_LL(A) :
B = A.left
A.left = B.right
B.right = A
return B
- 노드 레퍼런스가 3번 변경되었다.
RR - 회전
1
2
3
4
5
6
7
8
# RR - 회전 정의
## RR
def rotate_RR(A) :
B = A.right
A.right = B.left
B.left = A
return B
RL - 회전
1
2
3
4
5
6
7
# RL - 회전 정의
# RL
def rotate_RL(A) :
B = A.right
A.right = rotate_LL(B)
return rotate_RR(A)
LR - 회전
1
2
3
4
5
6
7
# LR - 회전 정의
# LR
def rotate_LR(A) :
B = A.left
A.left = rotate_RR(B)
return rotate_LL(A)
AVL 트리 노드, 재균형 연산 정의
AVL 트리 노드
- 이진탐색트리 노드에 height(노드 높이) 속성이 추가되었다.
1
2
3
4
5
6
7
8
9
# AVL 트리 노드 정의
class Node :
def __init__(self, key, value, height, left=None, right=None) :
self.key = key
self.value = value
self.left = left
self.right = right
self.height = height # 추가된 속성
서브트리 높이 차 정의
- 루트 왼쪽 서브트리 높이 - 루트 오른쪽 서브트리 높이
- 루트 왼쪽 자식 노드 height 속성 값 - 루트 오른쪽 자식 노드 height 속성 값
1
2
3
4
# 서브트리 높이 차 정의
def height_diff(n) :
return height(n.left) - height(n.right) # 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
트리 높이 정의
- 높이 구하려는 트리 루트노드의 height 값
- 루트노드가 비어있으면 높이는 0
1
2
3
4
5
6
# 서브트리 높이 정의
def height(n) :
if n == None : # 공트리면 높이 0
return 0
return n.height
재균형 연산 정의
- 왼쪽이 더 높고, 왼쪽이 더 높으면 LL - 회전
- 왼쪽이 더 높고, 오른쪽이 더 높으면 LR - 회전
- 오른쪽이 더 높고, 왼쪽이 더 높으면 RL - 회전
- 오른쪽이 더 높고, 오른쪽이 더 높으면 RR - 회전
1
2
3
4
5
6
7
8
9
10
11
12
13
# 재균형 연산 정의
def rebalance(parent) :
if height_diff(parent) > 1 : # 왼쪽 서브트리가 오른쪽 서브트리 보다 2 이상 높을 때
if height_diff(parent.left) > 0 : # 왼쪽 안에서 왼쪽이 더 큰 경우
parent = rotate_LL(parent)
elif height_diff(parent.left) < 0 : # 왼쪽 안에서 오른쪽이 더 큰 경우
parent = rotate_LR(parent)
elif height_diff(parent) < -1 : # 오른쪽 서브트리가 왼쪽보다 절댓값 2 이상 높을 때
if height_diff(parent.right) > 0 :
parent = rotate_RL(parent)
elif height_diff(parent.right) < 0 :
parent = rotate_RR(parent)
return parent
노드 삽입연산
노드 삽입 + 재균형 작업 한 세트다.
- 노드 삽입은 이진탐색트리와 같은 방법으로 이루어진다. (탐색 - 탐색 실패하면 그 자리 노드 삽입)
- 삽입한 노드부터 루트R로 거슬러 올라가며 각 서브트리 단위에서 재균형 작업 수행한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 노드 삽입연산 정의
def insert(parent, node) : # 키 비교할 노드, 삽입할 노드
if (parent.key > node.key) :
if parent.left == None :
parent.left = node
else :
parent.left = insert(parent.left, node)
return rebalance(parent) # 균형유지 후 루트 반환
elif (parent.key < node.key) :
if parent.right == None :
parent.right = node
else :
parent.right = insert(parent.right, node)
return rebalance(parent)
else :
print('중복된 키 에러. 삽입실패') # 탐색 실패
노드 삽입연산 예
10, 20, 30, 5, 3, 25, 28, 50, 40 을 AVL 트리에 순서대로 삽입하는 경우

노드 삭제연산
노드 삭제 + 재균형 작업 한 세트다.
- 노드 삭제는 이진탐색트리와 같은 방법으로 이루어진다. (탐색 - 키 찾으면 그 노드 삭제. 자식 0개냐, 1개냐, 2개냐에 따라 삭제방법 다름)
- 노드 삭제된 자리부터 루트R로 거슬러 올라가며 각 서브트리 단위에서 재균형 작업 수행한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 노드 삭제연산 정의
def del_node(self, n, key) :
if n == None :
return None # 삭제할 노드가 트리 안에 없음
if (n.key > key) :
n.left = self.del_node(n.left, key)
elif (n.key < key) :
n.right = self.del_node(n.right, key)
else : # 삭제할 노드 찾은 경우
if n.right == None : # 0, 1
return n.left
elif n.left == None :
return n.right # 1
else : # 2
target = n
n = self.minimum(target.right) # 중위후속자 = 오른쪽 서브트리 가장 왼쪽 값(최솟값)
n.right = self.del_min(target.right)
n.left = target.left
n.height = max(self.height(n.left), self.height(n.right)) + 1 # n의 높이 조정
return self.balance(n)
AVL 트리 성능
연산(탐색, 삽입, 삭제) 시간복잡도가 항상 $O(\log{n})$ 보장된다.
- AVL 트리 높이에 비례한다
AVL 트리 구현
AVL 트리 노드 정의
1
2
3
4
5
6
7
8
# 노드 정의
class Node :
def __init__(self, key, value, height, left=None, right=None) :
self.key = key
self.value = value
self.height = height
self.left = left
self.right = right
AVL 트리 객체 정의
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
# AVL트리 클래스
class AVL :
def __init__(self) :
self.root = None
# 노드 높이 정의
def height(self, n) :
if n == None :
return 0
return n.height
# 삽입연산 정의
def put(self, key, value) :
self.root = self.put_item(self.root, key, value)
def put_item(self, n, key, value) :
if n == None :
return Node(key, value, 1)
if (n.key > key) :
n.left = self.put_item(n.left, key, value)
elif (n.key < key) :
n.right = self.put_item(n.right, key, value)
else :
n.value = value # 키는 일치. 현재 노드 값 갱신
n.height = max(self.height(n.left), self.height(n.right)) + 1 # 루트 높이 갱신
return self.balance(n) # 루트 반환
# 불균형 처리 정의
def balance(self, n) :
if self.bf(n) > 1 : # 왼쪽 서브트리가 오른쪽 보다 높은 경우
if self.bf(n.left) < 0 : # LR
n.left = self.rotate_left(n.left)
n = self.rotate_right(n) # LL
elif self.bf(n) < -1 : # 오른쪽 서브트리가 왼쪽보다 높은 경우
if self.bf(n.right) > 0 : # RL
n.right = self.rotate_right(n.right)
n = self.rotate_left(n) # RR
return n
# 서브트리 높이 비교 정의
def bf(self, n) :
return self.height(n.left) - self.height(n.right)
# 오른쪽으로 회전 정의
def rotate_right(self, n) :
x = n.left
n.left = x.right
x.right = n
n.height = max(self.height(n.left), self.height(n.right)) + 1
x.height = max(self.height(x.left), self.height(x.right)) + 1
return x
# 왼쪽으로 회전 정의
def rotate_left(self, n) :
x = n.right
n.right = x.left
x.left = n
n.height = max(self.height(n.left), self.height(n.right)) + 1
x.height = max(self.height(x.left), self.height(x.right)) + 1
return x
# 노드 삭제 연산 정의
def delete(self, key) :
self.root = self.del_node(self.root, key)
def del_node(self, n, key) :
if n == None :
return None # 삭제할 노드가 트리 안에 없음
if (n.key > key) :
n.left = self.del_node(n.left, key)
elif (n.key < key) :
n.right = self.del_node(n.right, key)
else : # 삭제할 노드 찾은 경우
if n.right == None : # 0, 1
return n.left
elif n.left == None :
return n.right # 1
else : # 2
target = n
n = self.minimum(target.right) # 중위후속자 = 오른쪽 서브트리 가장 왼쪽 값(최솟값)
n.right = self.del_min(target.right)
n.left = target.left
n.height = max(self.height(n.left), self.height(n.right)) + 1 # n의 높이 조정
return self.balance(n)
# 최솟값(가장 왼쪽 노드) 삭제 정의
def delete_min(self) :
if self.root == None :
print(f'트리가 비어 있음')
self.root = self.del_min(self.root)
def del_min(self, n) :
if n.left == None :
return n.right
n.left = self.del_min(n.left)
n.height = max(self.height(n.left), self.height(n.right)) + 1 # 높이 갱신
return self.balance(n)
# 최솟값 찾기 정의
def min(self) :
if self.root == None : # 공트리면
return None
return self.minimum(self.root)
def minimum(self, n) :
if n.left == None :
return n # 최소 키 가진 노드
return self.minimum(n.left)
# 전위순회
def preorder(self, n) :
if n != None :
print(str(n.key), end=' ')
if n.left :
self.preorder(n.left)
if n.right :
self.preorder(n.right)
# 중위순회
def inorder(self, n) :
if n != None :
if n.left != None :
self.inorder(n.left)
print(str(n.key), end=' ')
if n.right != None :
self.inorder(n.right)
AVL 트리 객체가 잘 동작하는 지 테스트
노드 삽입
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 삽입연산
if __name__ == '__main__' :
t = AVL()
# 데이터 삽입
t.put(75, 'apple')
t.put(80, 'grape')
t.put(85, 'lime')
t.put(20, 'mango')
t.put(10, 'strawberry')
t.put(50, 'banana')
t.put(30, 'cherry')
t.put(40, 'orange')
t.put(70, 'melon')
t.put(90, 'plum')
전위순회
1
2
3
4
5
# 전위순회
if __name__ == '__main__' :
print(f'전위순회:\t', end=' ')
t.preorder(t.root)
전위순회: 75 40 20 10 30 50 70 85 80 90
중위순회
1
2
3
4
5
# 중위순회
if __name__ == '__main__' :
print(f'중위순회:\t', end=' ')
t.inorder(t.root)
중위순회: 10 20 30 40 50 70 75 80 85 90
75와 85 삭제
1
2
3
4
5
# 삭제연산
if __name__ == '__main__' :
t.delete(75)
t.delete(85)
삭제 후 전위순회
1
2
3
4
# 전위순회
if __name__ == '__main__' :
t.preorder(t.root)
40 20 10 30 80 50 70 90
삭제 후 중위순회
1
2
3
4
# 중위순회
if __name__ == '__main__' :
t.inorder(t.root)
10 20 30 40 50 70 80 90
80 삭제
1
2
3
# 삭제연산
t.delete(80)
80 삭제 후 전위순회
1
2
3
# 전위순회
t.preorder(t.root)
40 20 10 30 70 50 90
80 삭제 후 중위순회
1
2
3
# 중위순회
t.inorder(t.root)
10 20 30 40 50 70 90
위 과정이 제대로 이루어진 건지 알아보기 위해, 직접 손으로 그려가며 검증해 보았다.
75, 80, 85, 20, 10, 50 삽입

30, 40, 70, 90 삽입

전위순회)
75, 40, 20, 10, 30, 50, 70, 85, 80, 90
중위순회)
10, 20, 30, 40, 50, 70, 75, 80, 85, 90
75와 85 삭제 후)
75 삭제 >
원래 트리가 이랬다.

75 삭제는 자식 2개인 노드를 삭제하는 거다.
따라서 중위순회 후속자를 찾아서 75 자리를 대체해줘야 한다.
위 중위순회 결과를 보면 80이 75의 중위순회 후속자다.
80을 75 자리에 대체하면 트리가 아래와 같아진다.

이후 80이 지워진 자리부터 루트 방향으로 올라가면서 불균형 여부를 검사했다.
85 $\Rightarrow$ 불균형 없음
80 $\Rightarrow$ 불균형 없음
85 삭제 >
85는 오른쪽 자식 1개 있는 노드다. 이진탐색트리 노드 삭제 규칙에 따라, 85가 지워진 자리에 그 오른쪽 자식 90이 채워진다.
따라서 결과는 아래와 같다.

90부터 루트로 올라가면서 불균형 여부를 검사한다.
80 $\Rightarrow$ 불균형 있음. 왼쪽 서브트리가 더 높다.
왼쪽 서브트리가 더 높아 불균형 발생했으므로, 오른쪽으로 회전시켜야 한다.
$\Rightarrow$ rotate_right()
서브트리가 모두 오른쪽으로 회전하고, 결과는 아래와 같다.

전위순회)
40 20 10 30 80 50 70 90
중위순회)
10 20 30 40 50 70 80 90
80 삭제)
80은 자식이 2개 있는 노드다. 위 중위순회 결과를 보면 80의 중위 후속자는 90 이다.
90으로 80 자리 대체한다.

90부터 루트로 올라가며 불균형 여부 검사한다.
90 $\Rightarrow$ 불균형 있다. 왼쪽 서브트리가 더 높고, 왼쪽 안에서는 오른쪽 서브트리가 더 높다.
$\Rightarrow$ LR - 회전
LR - 회전 과정과 결과는 아래와 같다.

전위순회)
40 20 10 30 70 50 90
중위순회)
10 20 30 40 50 70 90
