[수학/선형대수] 주성분분석 (PCA)

잠재변수

정의 :

기저에 숨어서 여러 확률변수에 영향. 여러 확률변숫값을 동시에 결정짓는 확률변수

특징 :

직접 데이터 획득이 불가능하다.

---

측정데이터와 잠재변숫값 사이 관계

저차원벡터공간 기저벡터가 모두 단위벡터이고 정규직교한다고 하자.

이때, 저차원벡터공간에 대한 투영벡터는 다음과 같이 나타낼 수 있다.

예) 1차원

$x^{\Vert W} = [w_{1}][(x_{i}^{T}w_{1})]^{T}$

예) 2차원

$x^{\Vert W} = [w_{1}, w_{2}][(x_{i}^{T}w_{1}),(x_{i}^{T}w_{2})]^{T}$

예) 3차원

$x^{\Vert W} = [w_{1}, w_{2}, w_{3}][(x_{i}^{T}w_{1}),(x_{i}^{T}w_{2}), (x_{i}^{T}w_{3})]^{T}$

특정 기저벡터 공간 상에서 벡터의 좌표는 기저벡터 선형조합에서 각 기저벡터 스칼라 계수와 같다.

즉, 3차원이면 $[(x_{i}^{T}w_{1}),(x_{i}^{T}w_{2}), (x_{i}^{T}w_{3})]^{T}$ 이 부분이 3차원 기저벡터 상 투영벡터의 좌표다.

한편, 위 식을 전개하면 $[(x_{i}^{T}w_{1}),(x_{i}^{T}w_{2}), (x_{i}^{T}w_{3})]^{T}$ 이 부분은 각 기저벡터 $w_{i}$ 의 가중치와 같다.

저차원 공간 상에서 투영벡터 각 좌표 = 각 기저벡터가 투영벡터에서 차지하는 비중(가중치)

저차원 공간 기저벡터 하나하나는 주성분벡터와 같았다.

그러면

각 기저벡터 가중치 = 투영벡터에서 각 주성분벡터 비중

이다.

이 주성분벡터 비중을 잠재변숫값으로 본다.

결론적으로

잠재변숫값 1개 = $(x^{T}w_{i})$ 이다.

우변을 전개하면

잠재변숫값 1개 = $ax_{1} + bx_{2}$ 이다.

$x_{1}, x_{2}$ 는 $x_{i}$ 벡터가 담고 있던 측정데이터 1,2 다.

$a,b$는 기저벡터 i의 각 요소다. 고정되어 있다.

이를 통해 잠재변숫값은 측정데이터와 선형관계를 맺고 있다는 사실을 알 수 있다.

$+$ 위 선형방정식에서는 측정데이터 $x_{1}, x_{2}…$ 별 가중치가 정해져 있다.

이 가중치들은 각 변수들이 잠재변숫값에서 차지하는 비중이라 볼 수도 있다.

만약 위 선형방정식이 다음과 같다고 해보자.

$\mu = 0.96x_{1}+0.27x_{2}$

$x_{1}$ 은 잠재변숫값에서 0.96만큼의 비중을 차지할 것이다. $x_{2}$ 는 0.27만큼 비중을 차지할 것이다.

잠재변숫값이 증가하거나 감소할 때, $x_{1}, x_{2}$ 도 대략 0.96 : 0.27의 비율을 유지하면서 증가, 감소할 것이다.

잠재변수와 측정데이터 간 선형관계로 데이터가 규칙적으로 변이하는 이유를 설명할 수 있다.

역으로, 데이터가 규칙성 가지고 변이한다면 기저에 잠재변수가 있기 때문일 수 있다.

데이터가 규칙성 갖고 변이 할 때 PCA를 시도해 볼 수 있는 이유다.

---

여러 확률변수에 동시에 영향 미치는 공통 잠재변수가 있는 것으로 보일 때 주성분분석PCA 를 시도할 수 있다.

주성분분석PCA 목표와 의의

목표 :

다변수확률변수 데이터를 통해.

다변수확률변수가 어떤 공통 잠재변수(들)의 영향을 받았고,

해당 데이터는 어떤 잠재변수 영향을 얼만큼 받은 데이터인지 알아내는 것.

의의 :

다변수확률변수 데이터는 보통 2차원 이상의 고차원데이터이다.

PCA를 통해 복잡해보이는 고차원데이터 변이를 몇 가지 요인(잠재변수)들 만 가지고 간단히 설명 가능하다.

---

주성분분석PCA (차원축소)

정의 :

고차원데이터(벡터)와 가장 비슷한 저차원투영벡터를 찾고(차원축소),

이 투영벡터를 만드는 ‘저차원공간 기저벡터’를 찾는 과정이다.

곧, 랭크-K 근사 문제를 푸는 것 = PCA 분석이다.

전제 :

잠재변수 = 주성분

(물론 완전히 똑같지는 않다. 하지만 비슷한 개념으로 이해했다.)

따라서 주성분을 찾아야 잠재변수를 찾는 것이다.

분석 :

공통 잠재변수 영향 받는 것으로 보이는 고차원 데이터에 적용.

고차원데이터를 저차원공간에 투영시켜 가장 비슷한 투영벡터를 만든다.

이 투영벡터는 각 데이터의 공통부분, 노이즈를 제거하고 주성분으로만 구성된 벡터다. (주성분 선형조합으로 구성되어있다.)

각 투영벡터마다 주성분이 얼만큼씩 들었는가를 찾아낸다.

주성분은 원래 고차원 데이터를 구성하고, ‘결정’짓는 핵심성분이라 할 수 있다.

투영벡터 별 주성분 비중을 찾아냄으로써 원래 고차원데이터가 어떤 핵심성분이 얼마나 들어있었는지 알아낸다.

한편, 찾아낸 주성분을 통해 각 고차원데이터를 주성분 만으로 ‘설명’ 할 수 있다.

예)

올리베티 얼굴 이미지 데이터 : 이 데이터는 미소를 결정짓는 주성분 1이 7.5 만큼, 찡그린 표정을 결정짓는 주성분 2가 -9.9 만큼 들어있는 데이터다.

이 이미지 속 인물이 다른 이미지에 비해 크게 미소짓고 있는 이유는 1번 주성분이 매우 많이 들어가고, 2번 주성분이 매우 적게 들어있기 때문이다.

사이킷런 PCA 클래스

from sklearn.decomposition import PCA

pca = PCA(n_components=n)

• pca 변수는 PCA 클래스로 생성한 객체다.
• n_components= 에 주성분 몇 개를 찾을 건지 넣어주면 된다. (몇 차원 공간에 투영할 건지 입력한다)

PCA 클래스의 주요 속성과 메서드

pca.components_ #1.

pca.mean_ #2.

pca.fit_transform(특징행렬) #3.

pca.inverse_transform(좌표변환 된 저차원투영벡터) #4.

속성

• pca.components_ : 주성분벡터 (저차원공간 기저벡터)
• pca.mean_ : 특징행렬 데이터들의 평균벡터

메서드

• pca.fit_transform(특징행렬) : ‘평균 제거’한 고차원데이터들을 저차원투영벡터로 만들고, 좌표변환까지 해서 반환한다. (차원축소)

• pca.inverse_transform(fit_transform 결과물) : fit_transform 해서 차원축소된 고차원데이터의 저차원투영벡터를. 고차원기저벡터 기준.으로 다시 좌표변환한다. 그리고 처음에 제거했던 평균을 더해서 반환한다.

---

PCA 분석하기

1. 붓꽃 데이터 PCA 분석하기

붓꽃 꽃받침 길이, 꽃받침 폭만 가지고 PCA 분석을 해보자.

데이터 살펴보기

두 데이터를 먼저 한번 살펴보자.

from sklearn.datasets import load_iris
iris = load_iris().data

N = 10

X = iris[:N,:2]
plt.plot(X.T, 'o:')
plt.xticks(range(4), ['꽃받침 길이', '꽃받침 폭', '',''])
plt.xlim(-0.5,2)
plt.ylim(2.5, 6)
plt.title('꽃받침 길이-꽃받침 폭 크기 특성')
plt.legend([f'표본 {i+1}' for i in range(N)])
plt.show()

위 그래프에서 두 확률변수에서 얻은 데이터 사이 관계를 보자.

대체로 꽃받침 길이가 증가하면, 꽃받침 폭도 함께 증가했다.

혹은 꽃받침 폭이 증가하면, 꽃받침 길이가 증가했다.

두 확률변수 사이에는 상관관계가 있는 것으로 보인다.

df = pd.DataFrame(X, columns=load_iris().feature_names[0:2])
sns.scatterplot(x='sepal length (cm)', y='sepal width (cm)', data=df)

위 스캐터 플롯으로 봐도 마찬가지다. 한 개 확률변숫값이 증가하면, 다른 확률변숫값도 증가했다.

두 확률변수 사이 선형상관관계가 있는 건 확실해 보인다.

X_0 = X[:,0]
X_1 = X[:,1]

sp.stats.pearsonr(X_0, X_1)[0]

피어슨상관계수 값 : $0.7872066124624175$

한편, 위 두 그래프를 보면 두 확률변숫값들의 비율은 대체로 일정함을 알 수 있다.

종합하면, 두 확률변숫값들은 대체로 일정한 비율을 유지하며 함께 변화한다.

이렇게 데이터 변이에 규칙성이 보일 때, 데이터들에 공통 잠재변수가 작용하고 있는 것은 아닌지 의심해볼 수 있다.

데이터들에 작용하고 있는 공통 잠재변수와, 각 잠재변수 값들을 알아내는 방법이 PCA였다.

PCA 분석 수행하기

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
X_low = pca.fit_transform(X)
X_low # 좌표변환된 1차원 투영벡터들

기저에서 전체 데이터에 영향 미치고 있는 1개 주성분만 찾아보자. PCA 클래스 n_components 인자에 1을 넣으면 1차원에 벡터들을 근사시켜준다.

결과

array([[ 0.30270263],
       [-0.1990931 ],
       [-0.18962889],
       [-0.33097106],
       [ 0.30743473],
       [ 0.79976625],
       [-0.11185966],
       [ 0.16136046],
       [-0.61365539],
       [-0.12605597]])

결과로 나온 위 행렬 각 행이 좌표변환한 1차원 투영벡터들이다.

고차원 데이터를 차원축소시켜서 나오는 위 결과물은 각 잠재변수(주성분)가 1개 데이터 레코드마다 얼만큼 들어있는지 나타내기도 한다.

위 결과물을 보니 첫번째 표본은 두번째 표본보다 주성분이 크게 작용하고 있음을 볼 수 있다.

주성분 벡터

전체 데이터레코드 기저에서 작용하고 있는 주성분은 다음과 같았다.

pca.components_[0]

$array([0.68305029, 0.73037134])$

이 주성분은 특징행렬의 고차원데이터들과 가장 비슷한 저차원 투영벡터들을 만들어내는 저차원공간의 기저벡터다.

PCA는 랭크-K문제를 푸는 것과 같다고 했다.

랭크-K 문제에서는 가장 비슷한 투영벡터들 만들어내는 저차원공간 기저벡터가

가장 큰 K개 특잇값에 대응되는 특징행렬 오른쪽 특이벡터들.

또는 특징행렬로 만든 분산행렬에서 가장 큰 K개 고윳값에 대응되는 고유벡터들 과 같았다.

PCA 클래스를 통해서 구한 주성분벡터(=저차원공간 기저벡터) 가 특징행렬의 특이벡터 또는 분산행렬 고유벡터와 같은지 직접 알아보자.

1. 오른쪽 특이벡터와 주성분 벡터가 같은가?

# 증명해보자. 
# 1. 특잇값분해 
X0 = X-X.mean(axis=0)

U, S, VT = np.linalg.svd(X0)

-VT.T[:,0]

array([0.68305029, 0.73037134])

PCA 통해 주성분을 1개만 찾았기 때문에, 내가 찾은 주성분은 가장 큰 특잇값에 대응하는 오른쪽 첫번째 특이벡터일 것이다.

PCA에서는 근사성능을 높이기 위해 특징행렬 데이터에서 평균값들을 제거하고 남은 데이터로 저차원 투영한다.

따라서 특이벡터 찾을 때도

맨 처음 특징행렬 $X$ 에서 평균값들을 제거한 것을 특징행렬로 써서 특잇값분해 한 뒤 특이벡터를 찾았다.

특징행렬 $X0$를 특잇값분해 한 뒤, 오른쪽 첫번째 특이벡터를 구해서 주성분벡터와 비교했더니 같았다.

2. 분산행렬 고유벡터와 주성분 벡터가 같은가?

# 2. 고유분해 
XTX = X0.T@X0
ld, V = np.linalg.eig(XTX)
-V[:, np.argmax(ld)]

한편 평균 제거한 특징행렬로 만든 분산행렬 $X^{T}X$ 를 만들었다. 특잇값분해 - 고윳값분해 사이 관계에 의해서 오른쪽 특이벡터 행렬은 고유벡터 행렬과 같았다.

오른쪽 특이벡터 행렬에서 첫번째 특이벡터가 주성분 벡터와 같았다.

그러면 고유벡터 행렬에서 첫번째(가장 큰 고윳값에 대응) 고유벡터가 주성분 벡터와 같을 것이다.

파이썬 eig() 명령으로 분산행렬을 고윳값분해 한 뒤, 가장 큰 고윳값에 대응되는 고유벡터를 찾았다.

array([0.68305029, 0.73037134])

역시 주성분 벡터와 같았다.

---

붓꽃 주성분의 의미

앞에서 PCA를 통해 붓꽃 데이터의 주성분을 찾아냈다.

pca.components_[0]

array([0.68305029, 0.73037134])

그리고 fit_transform() 을 통해 각 데이터 레코드에 이 주성분이 얼마나 들어있는지(주성분비중) 도 찾아냈다.

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
X_low = pca.fit_transform(X)
X_low # 1차원 투영벡터들

array([[ 0.30270263],
       [-0.1990931 ],
       [-0.18962889],
       [-0.33097106],
       [ 0.30743473],
       [ 0.79976625],
       [-0.11185966],
       [ 0.16136046],
       [-0.61365539],
       [-0.12605597]])

첫번째 데이터레코드에는 두번째보다 상대적으로 많이 들어있는 이 주성분의 의미는 뭘까?

위 주성분 비중은 측정데이터와 선형관계를 가진다.

예를 들어 첫번째 데이터에서 주성분비중과 측정데이터 관계는 다음과 같다.

첫번째 측정 데이터

X-pca.mean_[0]

$[ 0.24, 0.19]$

$0.30270263 = [ 0.24, 0.19][0.68305029, 0.73037134]^{T}$

$ 0.30270263 = 0.68 \times (0.24) + 0.73 \times (0.19) $

괄호 안이 측정데이터다.

잠재변숫값이 꽃잎 길이와 꽃잎 폭의 선형조합 결과로 나온다. 곧, 이 잠재변수는 ‘꽃 크기’ 임을 추측해볼 수 있다.

이렇게 결론 내리고 다시 맨 처음 특징행렬 데이터로 돌아가보자.

특징행렬 데이터

array([[ 0.24,  0.19],
       [ 0.04, -0.31],
       [-0.16, -0.11],
       [-0.26, -0.21],
       [ 0.14,  0.29],
       [ 0.54,  0.59],
       [-0.26,  0.09],
       [ 0.14,  0.09],
       [-0.46, -0.41],
       [ 0.04, -0.21]])

(평균이 제거되어 있다.)

주성분 비중 데이터

array([[ 0.30270263],
       [-0.1990931 ],
       [-0.18962889],
       [-0.33097106],
       [ 0.30743473],
       [ 0.79976625],
       [-0.11185966],
       [ 0.16136046],
       [-0.61365539],
       [-0.12605597]])

이렇게 결론내릴 수 있다.

첫번째 데이터레코드(특징행렬 1행) 는 ‘꽃 크기’라는 주성분 비중이 크다. 곧, 꽃잎 길이와 꽃잎 폭이 모두 다른 데이터레코드보다 큰 이유는 꽃 크기가 커서 그렇다.

---

이미지 PCA

이번에는 올리베티 얼굴사진 데이터에 PCA 분석을 해보자.

얼굴사진 데이터를 PCA 분석하면, 얼핏 비슷비슷해보이는 각 이미지 데이터들의 차이를 결정짓는 몇 가지 핵심성분을 뽑아낼 수 있을 것이다.

이 과정을 통해

데이터를 구성하는 핵심 성분이 뭔지,

이게 어떻게 작용하면서 각 데이터 간 차이를 만들어내는지 분석할 수 있다.

from sklearn.datasets import fetch_olivetti_faces

K = 21
faces_all = fetch_olivetti_faces()
face_data = faces_all.data[faces_all.target == K]

fig = plt.figure(figsize=(10,5))
plt.subplots_adjust(top=1, bottom=0, hspace=0, wspace=0.05)

for i in np.arange(0,10) : 
    plt.subplot(2,5,i+1)
    plt.imshow(face_data[i].reshape(64,64), cmap=plt.cm.bone)
    plt.xticks([])
    plt.yticks([])
plt.suptitle('올리베티 얼굴 이미지 데이터')
plt.tight_layout()
plt.show()

데이터 살펴보기

각 얼굴이미지 데이터들은 64*64 행렬이다.

분석할 때는 10개 이미지 모두 각각 4096*1 사이즈 벡터로 변환시켜서, 10개 벡터로 특징행렬 하나를 만들 것이다.

구상하기

10개 이미지 데이터로 이루어진 특징행렬 1개를 가지고 분석할 것이다.

각 이미지 데이터는 특징행렬의 행벡터로 들어가 있다.

이 행벡터들을 PCA로 차원축소 시켜서, 각 데이터 평균을 제거하고, 노이즈도 제거하고, 주성분 만으로 구성할 것이다.

주성분들이 각 데이터를 구성하는 ‘핵심성분’이다. 주성분들은 모든 데이터에 공통적으로 들어있는데, 이들이 각 데이터에 얼만큼씩 들었느냐가 각 데이터 간 차이 결정한다.

주성분을 찾고, 데이터 별 주성분 비중을 통해 주성분 의미를 추측해보고, 주성분 비중을 조정시켜가며 이 주성분이 데이터에 어떤 영향 미치는지 알아보자.

그리고 각 주성분의 의미를 찾아내자.

분석하기

데이터에서 주성분 4개를 뽑아보자.

얼굴사진 데이터의 주성분을 ‘아이겐페이스(고유얼굴)’ 이라고도 한다.

이 주성분들이 실제로 고유벡터들이기도 하고, 인물사진 별로 고유의 아이겐페이스를 가지고 있기 때문에 ‘고유얼굴’ 이라고 부른다.

---

여기서부터는 내 추론이다. 좀 더 공부가 되고 난 뒤 추론 내용이 옳았는지 보려고 한다.

인물별로 고유의 아이겐페이스를 가지고 있을 것이다.

A라는 인물 얼굴사진을 여러장 찍으면 A 인물의 아이겐페이스 몇 개를 뽑아낼 수 있을 것이다.

B라는 인물 얼굴사진을 여러장 찍으면 B 인물의 아이겐페이스 몇 개를 뽑아낼 수 있을 것이다.

인물 A의 거의 모든 얼굴사진은 A에서 뽑아낸 아이겐페이스 선형조합으로 나타낼 수 있을 것이다.

B도 마찬가지다.

한편, 만약 어떤 얼굴 이미지를 얼굴인식기에 넣었는데 아이겐페이스 선형조합으로 표현되지 않는다면(오차가 매우 크다면) 인풋 사진은 A가 아닌 다른 인물의 사진일 가능성이 높다.

B도 마찬가지다.

그러면 인물 A와 B는 각 인물을 식별할 수 있는 고유의 특징얼굴을 갖고 있는 것이다.

이 ‘고유의 특징얼굴’을 ‘아이겐페이스(고유얼굴)’ 이라고 한다.

---

다시 돌아와서, 동일인물 얼굴사진 10개의 아이겐페이스 4개를 뽑아내보자.

mean_face = pca4.mean_
component1 = pca4.components_[0]
component2 = pca4.components_[1]
component3 = pca4.components_[2]
component4 = pca4.components_[3]

face_list = [mean_face, component1, component2, component3, component4]
face_name_list = ['mean', 'component1', 'component2', 'component3', 'component4']

for i in range(5) : 
    plt.subplot(1,5,i+1)
    plt.imshow(face_list[i].reshape(64,64), cmap=plt.cm.bone)
    plt.xticks([])
    plt.yticks([])
    plt.title(face_name_list[i])
plt.suptitle('평균 얼굴과 아이겐페이스 1,2,3,4')
plt.tight_layout()
plt.show()

가장 왼쪽은 ‘평균얼굴’(모든 데이터 공통성분)

그리고 왼쪽에서 오른쪽 순서로 주성분1, 주성분2, 주성분3, 주성분4 이다.

1~4 주성분은 벡터 형태다. 지금은 이미지로 표현하기 위해 64*64 사이즈 행렬로 변환된 것이다.

각 아이겐페이스의 의미를 보자.

먼저 1번 주성분은 어떤 의미를 갖는지 보자.

# 1번 주성분
w = np.linspace(5,10,10)
for i in range(10) : 
    plt.subplot(2,5,i+1)
    plt.imshow(mean_face.reshape(64,64)+w[i]*component1.reshape(64,64), cmap=plt.cm.bone)
    plt.xticks([])
    plt.yticks([])
    plt.title(f'주성분 1 비중 : {np.round(w[i],2)}')

plt.tight_layout()
plt.show()

첫번째 줄 왼쪽부터 두번째 줄 가장 오른쪽 10번째 이미지까지,

평균벡터(공통성분) 에 1번 주성분만 가중치를 변화시켜가며 더했다.

가중치 $w = [5,5.55, 6.11, 6.66, 7.22, 7.77, 8.33, 8.88, 9.44, 10]$

주성분 비중 변화에 따라 데이터가 어떻게 바뀌는지 보면, 이 주성분의 의미를 파악할 수 있을 것이다.

위 이미지는 왼쪽에서 오른쪽으로, 주성분 비중이 커진다.

(아쉽게도 VSCODE 상의 문제인지, 이미지별 title이 달리지 않았다)

이 주성분 비중이 커질 수록 인물이 눈을 감게 되는 것을 관찰할 수 있었다.

곧, 이 주성분은 이미지 속 인물이 눈을 뜨고 있느냐, 감고 있느냐 여부 결정하는 주성분이다.

이 주성분 비중이 높은 이미지 데이터는 인물이 눈을 감고 있을 것이다.

---

2번 주성분의 의미를 보자.

# 2번 주성분
w = np.linspace(-5,5,10)
for i in range(10) : 
    plt.subplot(2,5,i+1)
    plt.imshow(mean_face.reshape(64,64)+w[i]*component2.reshape(64,64), cmap=plt.cm.bone)
    plt.xticks([])
    plt.yticks([])
    plt.title(f'주성분 2 비중 : {np.round(w[i],2)}')

plt.tight_layout()
plt.show()

마찬가지로 평균얼굴에 2번 주성분만 비중을 변화시켜가며 더했다.

왼쪽에서 오른쪽으로 갈 수록 주성분 비중이 높아진다.

이 주성분 비중이 높아질 수록 인물이 미소짓게 된다.

곧, 2번 주성분은 인물이 미소짓고 있는가, 무표정한가 여부를 결정짓는 주성분이다.

이 주성분 비중이 높은 데이터는 인물이 미소짓고, 낮은 데이터 일 수록 인물이 무표정하고 있을 것이다.

---

3번 주성분의 의미를 보자.

# 3번 주성분
w = np.linspace(-5,5,10)
for i in range(10) : 
    plt.subplot(2,5,i+1)
    plt.imshow(mean_face.reshape(64,64)+w[i]*component3.reshape(64,64), cmap=plt.cm.bone)
    plt.xticks([])
    plt.yticks([])
    plt.title(f'주성분 2 비중 : {np.round(w[i],2)}')

plt.tight_layout()
plt.show()

평균얼굴에 3번 주성분 아이겐페이스 비중을 변화시켜가며 더했다.

이 주성분 비중이 높아질 수록 인물이 치아를 드러내고 있다.

반대로 주성분 비중이 낮을 수록 입술을 다물고 있다.

3번 주성분은 인물이 치아를 드러내고 있는가 여부를 결정짓는 주성분이다.

이 주성분이 높은 이미지 데이터일 수록 인물이 치아를 드러내고 있을 것이다. 낮은 데이터일 수록 인물이 입술을 다물고 있을 것이다.

---

마지막 4번 주성분의 의미를 살펴보자.

# 4번 주성분
w = np.linspace(-5,5,10)
for i in range(10) : 
    plt.subplot(2,5,i+1)
    plt.imshow(mean_face.reshape(64,64)+w[i]*component4.reshape(64,64), cmap=plt.cm.bone)
    plt.xticks([])
    plt.yticks([])
    plt.title(f'주성분 2 비중 : {np.round(w[i],2)}')

plt.tight_layout()
plt.show()

4번 주성분 비중이 높아질 수록 인물이 턱을 살짝 들고 있다.

반대로, 주성분 비중이 낮아질 수록 인물이 정면을 바라보고 있다.

4번 주성분은 인물이 정면 보고 있는가, 아니면 턱을 살짝 들고 있는가 여부를 결정하는 주성분이다.

---

주식 연간수익률 데이터 PCA

이번에는 미국, 인도, 멕시코, 독일, 이탈리아 5개 국가의 주식 연간 수익률 데이터를 가지고 PCA를 해보자.

먼저 1990년-2020년까지 31년간 5개 국가의 주가 데이터를 불러왔다.

pd.core.common.is_list_like = pd.api.types.is_list_like
import pandas_datareader.data as web
import datetime

symbols = [
    'SPASTT01USM661N',
    'SPASTT01INM661N',
    'SPASTT01MXM661N',
    'SPASTT01DEM661N',
    'SPASTT01ITM661N'
]

data = pd.DataFrame()
for sym in symbols : 
    data[sym] = web.DataReader(sym, data_source='fred',
    start=datetime.datetime(1990, 1,1),
    end=datetime.datetime(2020,12,31))[sym]
data.columns = ['US', 'IN', 'MX', 'DE', 'IT']
data = data/data.iloc[0]*100

styles = ['b-.', 'g--', 'c:', 'r-', 'k']
data.plot(style=styles)
plt.title('미국, 인도, 멕시코, 이탈리아,  30년간 주가')
plt.show()

주가 데이터를 연간 수익률 데이터로 바꾸자.

# 주식 연간수익률 데이터
df = ((data.pct_change() + 1).resample('A').prod()-1).T*100
print(df.iloc[:,:5])

이제 위 데이터를 가지고 PCA를 할 것이다.

위 데이터는 31차원 벡터 5개를 담고 있는 특징행렬이다.

각 31차원 벡터를 차원축소 시켜 주성분만으로 구성하고, 기저에서 어떤 주성분이 작용하고 있으며 국가별로 주성분이 얼만큼씩 작용하고 있는지 살펴보았다.

우선 31차원 벡터들을 살펴보자.

df.T.plot(style=styles)
plt.title('미국,인도,멕시코,독일,이탈리아 과거 30년간 수익률')
plt.xticks(df.columns)
plt.show()

5개 31차원 벡터 그래프로 그렸을 때, 형상이 비슷비슷함을 관찰할 수 있다.

특정 구간에서 올라가면 다음 구간에서 내려가고 하는 식이다.

즉, 5개 벡터 모두에서 데이터 변이가 규칙적으로 일어나고 있었다.

그러면 31차원 벡터의 각 확률변수 기저에 공통 잠재변수가 작용하고 있음을 추측해볼 수 있다.

공통 잠재변수 값(주성분 비중)이 큰가, 작은가에 따라 각 데이터가 달라질 것이다.

이 주성분을 찾아내고, 주성분의 의미를 파악해보자.

그리고 각 국가 데이터별로 주성분 비중이 얼만큼씩 인지도 파악해보자.

주성분은 1개를 찾겠다.

from sklearn.decomposition import PCA
pca5 = PCA(n_components=1) # 주성분 1개를 찾아보자. 
X_low = pca5.fit_transform(df)

m = pca5.mean_

pca5.components_

찾아낸 1개 주성분은 다음과 같다.

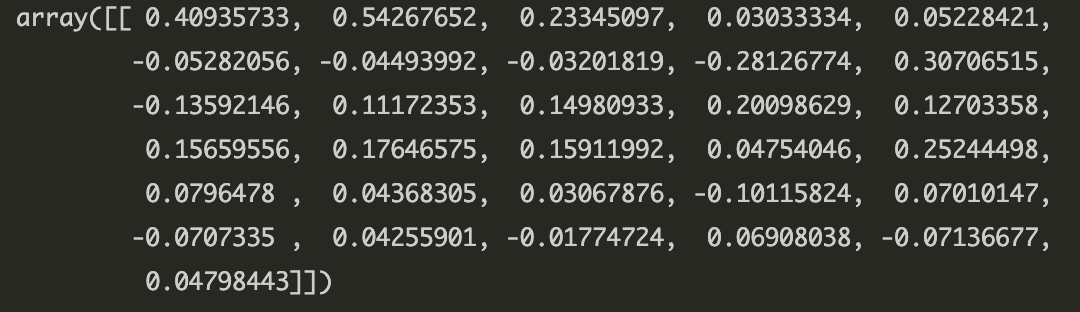
이제 이 주성분 비중 변화에 따라 데이터가 어떻게 변화하는지 살펴보자.

평균벡터를 기준으로 두고, 평균벡터에 주성분 비중을 증가시켜가며 더했다.

x_range = np.linspace(1990, 2020, 31, dtype=int)
for i in np.linspace(0,100,5) : 
    plt.plot(x_range, m+pcomponent1[0]*i)
plt.plot(x_range, m+pcomponent1[0]*100, label='주성분 100배')
plt.plot(x_range, m, 'ko-', lw=5, label='평균수익률')
plt.title('주성분 비중이 커질 때')
plt.legend()
plt.show()

주성분 비중이 커짐에 따라, 데이터가 평균보다 위쪽으로 증가함을 관찰할 수 있었다.

이제 그러면 평균에 주성분 비중을 감소시켜가며 더해보자.

즉, 주성분 비중을 줄여가는 것이다.

x_range = np.linspace(1990, 2020, 31, dtype=int)
for i in np.linspace(0,-100,5) : 
    plt.plot(x_range, m+pcomponent1[0]*i)
plt.plot(x_range, m+pcomponent1[0]*-100, label='주성분 -100배')
plt.plot(x_range, m, 'ko-', lw=5, label='평균수익률')
plt.title('주성분 비중이 작아질 때')
plt.ylim(-60, 80)
plt.legend()
plt.show()

주성분 비중이 작아질 수록, 평균을 기준점으로 점점 아래쪽으로 데이터가 형성됨을 관찰할 수 있었다.

주성분 변화 관찰 후 결론 :

• 이 주성분이 많아질 수록 데이터 형상이 평균에서 위쪽으로 변화한다.
• 이 주성분이 적어질 수록 데이터 형상이 평균에서 아래쪽으로 변화한다.

국가별 데이터의 주성분 비중

df_low = pd.DataFrame(X_low, columns=['주성분 비중'], index=['US','IN','MX','DE','IT'])
df_low

저차원 투영벡터의 저차원 공간 기저벡터 기준 좌표는 주성분 비중과 같았다.

위 표가 국가 데이터 별 주성분 비중이다.

미국, 독일, 이탈리아는 주성분 비중이 - 값이고(적고), 인도, 멕시코 데이터는 주성분 비중이 +값이었다(많다)

위에서 이 주성분이 + 방향으로 많아질 수록 데이터가 평균수준에서 위쪽으로 형성되었다.

반대로 주성분이 - 방향으로 많아질 수록 데이터가 평균수준에서 아래쪽으로 형성되었다.

미국, 독일, 이탈리아의 데이터는 평균수준에서 아래쪽으로 비슷비슷하게 형성되고,

인도. 멕시코의 데이터는 평균수준에서 위쪽으로 비슷비슷하게 형성될 것이다.

멕시코. 인도는 많고, 미국.독일.이탈리아는 비중이 적은 주성분이다.

---

fit_transform() 명령을 통해 31차원 데이터를 1차원 근사시킨 후, inverse_transform() 명령을 통해 다시 31차원으로 복귀시켰다.

복귀시킨 벡터는 31차원 저차원 투영벡터로, 노이즈가 제거되고 평균과 주성분1개 만으로 구성되어 있다.

사실상 데이터 별로 주성분 비중만 다르다.

실제 데이터가 어떻게 형성되는지 함 보자.

df2 = pd.DataFrame(pca5.inverse_transform(df_low))
df2.columns=df.columns
df2.index=df.index
df2.T.plot(style=styles)
plt.title('각 데이터에서 노이즈 제거하고 평균+주성분으로만 구성한 근사데이터')
plt.xticks(df.columns)
plt.show()

근사데이터들이 형성된 것을 보면, 앞에서 했던 예상이 맞았음을 볼 수 있다.

평균을 기점으로 이 주성분이 많을 수록 데이터 형상이 인도,멕시코와 유사하게 변할 것이다.

반대로 이 주성분이 적을 수록 데이터 형상이 미국, 독일, 이탈리아의 데이터와 비슷하게 변할 것이다.

인도, 멕시코를 개발도상국으로 놓고, 미국. 독일. 이탈리아를 선진국으로 둔다면, 이 주성분은 비중이 높아질 수록 데이터를 선진국 쪽에서 개도국 쪽으로 변화시키는 주성분이다.

곧, 이 주성분은 ‘개도국이냐. 아니냐’ 여부를 결정짓는 ‘개도국 요인’임을 알 수 있었다.