‘프로그래머가 알아야 할 알고리즘 40’(임란 아마드 지음, 길벗 출판사) 을 통해 정렬 알고리즘을 공부. 복습하고나서, 알고리즘을 구현하기 위해 문제를 정의내리고 해결책을 구상한 과정. 사고흐름. 구현 결과를 2022년 7월 20일 최초 기록한다.
버블정렬
정의
가장 큰 값을 가장 오른쪽으로 보내기
방법
이웃한 값 비교해서 교환(패스)
- 패스 N-1 번 반복
스니펫 구상
1
2
3
4
5
6
7
8
# 버블정렬 구상
for end in range(len(list), 0, -1) :
for i in range(0, end-1) :
# 1. 2개 비교
# 2. 만약 둘 중에 앞 값이 더 크면: 서로 자리 교체
# -->
if list[i] > list[i+1] :
list[i], list[i+1] = list[i+1], list[i]
구현
1
2
3
4
5
6
7
# 버블정렬 구현
def bubble_sort(x) :
for end in range(len(x)-1, 0, -1) :
for i in range(0,end) :
if x[i] > x[i+1] :
x[i], x[i+1] = x[i+1], x[i]
return x
테스트
1
2
x = [25, 21, 22, 24, 23, 27, 26]
bubble_sort(x)
[21, 22, 23, 24, 25, 26, 27]
삽입정렬
구상
- N-1번 중 이번회차에 대해서
- 이번 회사체 정렬해야 할 원소 위치: j
- 이번 회차에 정렬해야 할 원소의 값: temp
- while(j-1 >= 0) and (list[ j ] < list[ j-1 ]) : list[ j ] = list[ j-1 ], j-=1
- while 반복이 끝나면: list[ j ] = temp
스니펫
1
2
3
4
5
6
7
8
# 삽입정렬 스니펫
for n in range(1, len(x)) :
j = n
temp = x[j]
while (j-1 >= 0) and (temp < list[j-1]>) :
list[j] = list[j-1]
j-= 1
list[j] = temp
구현
1
2
3
4
5
6
7
8
9
10
11
# 삽입정렬 구현
def insert_sort(x) :
for n in range(1, len(x)) :
j = n # 정렬 해야 할 가장 왼쪽 위치
temp = x[j]
while (j-1 >= 0) and (temp<x[j-1]) :
x[j] = x[j-1]
j -= 1
x[j] = temp
return x
테스트
1
2
3
4
5
6
7
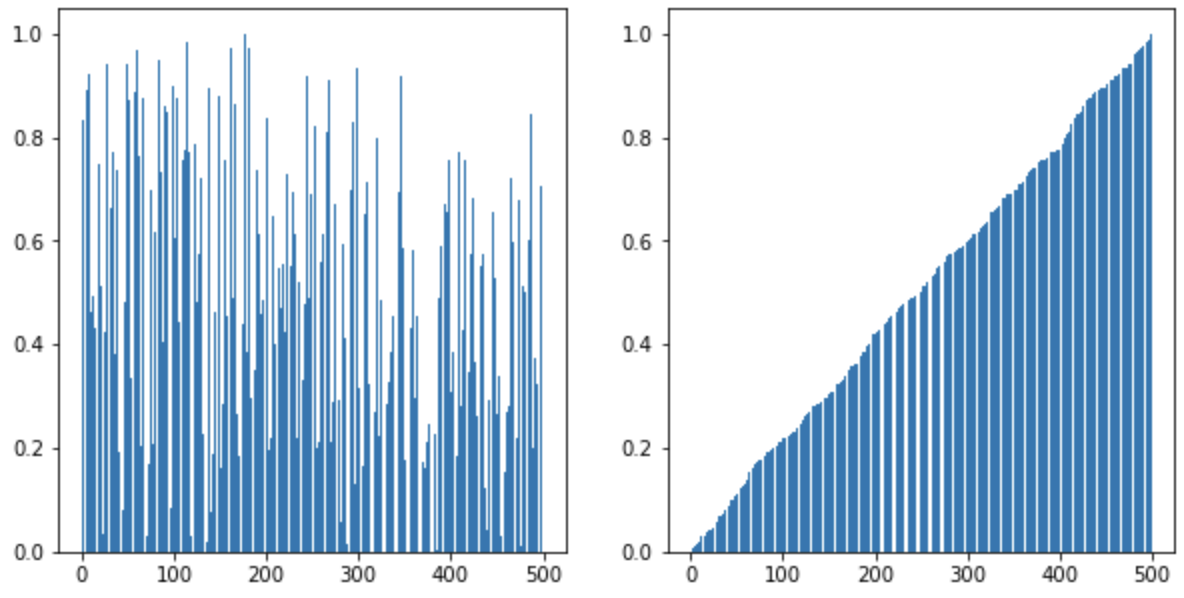
import numpy as np
import matplotlib.pyplot as plt
x = [25, 26, 22, 24, 27, 23, 21]
insert_sort(x)
x2 = list(np.random.sample(100))
plt.bar(range(100), insert_sort(x2))
병합정렬
구상
전체 과정은 분리 $\Rightarrow$ 병합.
<분리>
- 분리조건: 리스트 크기 $> 1$ 일 때; 리스트 크기 1 되면 분리 정지(=크기 1될 때 까지 분리)
- 분리 기준점 설정
- 분리 기준점 기준 왼쪽으로 분리
- 분리 기준점 기준 오른쪽으로 분리
왼쪽에 대해 다시 분리(+병합) 적용
오른쪽에 대해 다시 분리(+병합) 적용
<병합>
- 왼쪽 오른쪽 크기 비교해서, 오름차순으로 원본리스트에 결합
*분리된 상태 = 정렬된 상태.
a = 0 , 왼쪽 인덱스
b = 0 , 오른쪽 인덱스
c = 0 , 전체 인덱스
while (a < len(left)) and (b < len(right)) :
if left[ a ] > right[ b ] : list[ c ] = right[ b ], b+= 1
else: list[ c ] = left[ a ], a+= 1
c += 1
while (a < len(left)) : list[ c ] = left[ a ], a += 1, c+= 1
while (b < len(right)) : list[ c ] = right[ b ], b+= 1, c+= 1
return list, 정렬 결과 출력
구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 병합 정렬 구현
def merge_sort(x) :
# 분리
if len(x) > 1 : # 분리 조건
separate_criterion = len(x)//2
left = x[:separate_criterion]
right = x[separate_criterion:]
merge_sort(left)
merge_sort(right)
# 병합
a = 0
b = 0
c = 0
while (a < len(left)) and (b < len(right)) :
if left[a] > right[b] :
x[c] = right[b]
b += 1
else :
x[c] = left[a]
a += 1
c += 1
while (a < len(left)) :
x[c] = left[a]
a += 1
c += 1
while (b < len(right)) :
x[c] = right[b]
b += 1
c += 1
return x
테스트
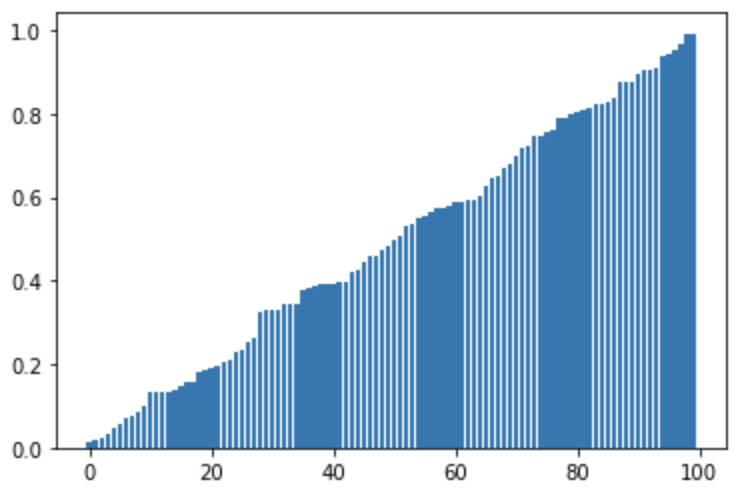
1
2
list3 = [44, 16, 83, 7, 67, 21, 34, 45, 10]
merge_sort(list3)
[7, 10, 16, 21, 34, 44, 45, 67, 83]
테스트 2
1
2
3
4
5
6
test = list(np.random.sample(100))
plt.figure(figsize=(100,50))
plt.subplot(1,2,1)
plt.bar(range(100), test)
plt.subplot(1,2,2)
plt.bar(range(100), merge_sort(test))
셸 정렬
삽입정렬 보완판.
구상
- 거리 설정한다.
- 정렬해야 할 원소 j와 j-distance 사이 값 비교한다.
- j < j-distance 이면, j와 j-distance 값 위치 교환 , j = j-distance 로 새로 할당
- 3의 과정을 j-distance >=0 일 때 까지 반복한다.
구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 셸 정렬 구현
def shell_sort(x) :
distance = len(x)//2 # 거리 지정
while distance > 0 :
# 부분 리스트 정렬 하는 코드 블럭
for i in range(distance, len(x)) :
j = i
# 부분리스트 1개에 대해 정렬하는 코드 블럭
while (j-distance >= 0) and (x[j] < x[j-distance]) :
x[j], x[j-distance] = x[j-distance], x[j]
j = j - distance
distance = distance // 2 # 다 끝났으면 거리 조정
return x
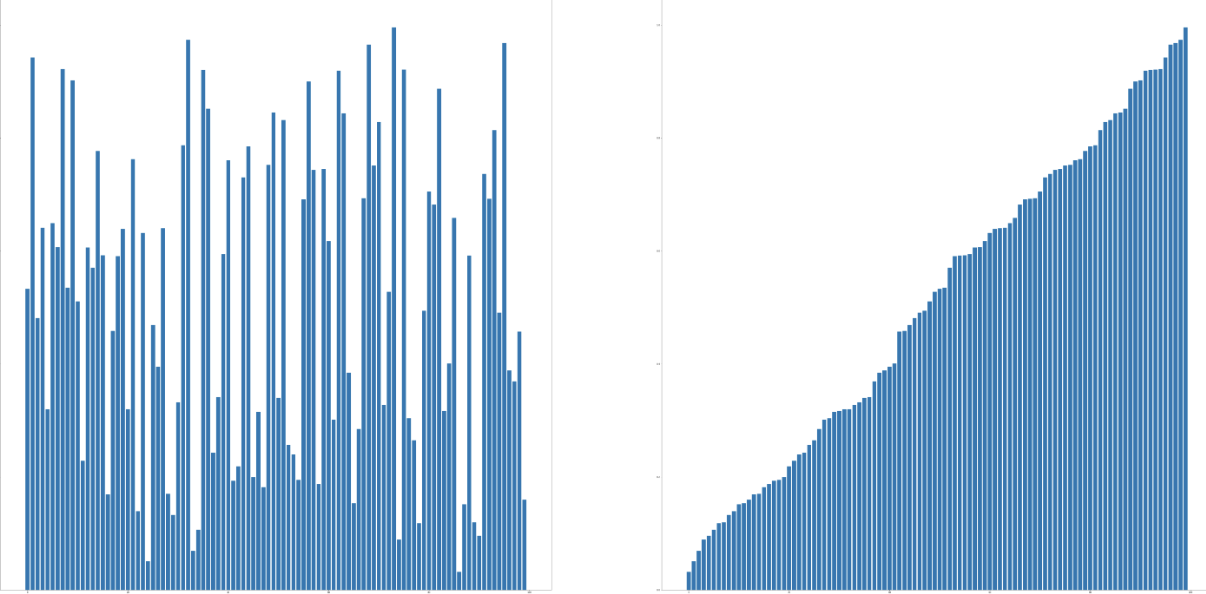
테스트
1
2
3
4
5
6
7
x = list(np.random.sample(100))
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.bar(range(100), x)
plt.subplot(1,2,2)
plt.bar(range(100), shell_sort(x))
plt.show()
선택정렬
구상
- 정렬 안 된 부분에서 가장 큰 값 찾아서, 정렬 안 된 부분 가장 오른쪽 원소와 바꾼다.
- 정렬 안 된 부분 가장 오른쪽 위치는 교환 발생할 때 마다, 1씩 줄어든다.
$\Rightarrow$
<다시 정리>
교환
- 정리 안 된 부분에서 가장 큰 값 찾는다.
- 가장 큰 값과, 정렬 안 된 부분 가장 오른쪽 원소 맞바꾼다.
+
- 교환 발생할 때 마다 ‘정렬 안 된 부분 가장 오른쪽 위치’가 1씩 줄어든다.
- 교환은 총 n-1번 발생한다.
스니펫
1
2
3
4
5
6
7
8
9
10
11
for r in range(len(x)-1, 0, -1) : # 가장 오른쪽 요소의 인덱스
# n-1번 교환 발생
#<가장 큰 값 찾기>
max_index = 0
for i in range(1, r+1) :
if x[max_index] < x[i] :
max_index = i
# 이제 가장 큰 값(그것의 인덱스) 찾았다. 교환한다.
# <교환>
x[max_index], x[r] = x[r], x[max_index]
구현
1
2
3
4
5
6
7
8
9
10
11
12
13
# 선택정렬 복습 & 구현
def selection_sort(x) :
for r in range(len(x)-1, 0, -1) : # 가장 오른쪽 요소의 인덱스 (1씩 감소)
# 가장 큰 값 찾기
max_index = 0
for i in range(1, r+1) :
if x[max_index] < x[i] :
max_index = i
# 교환
x[max_index], x[r] = x[r], x[max_index]
return x
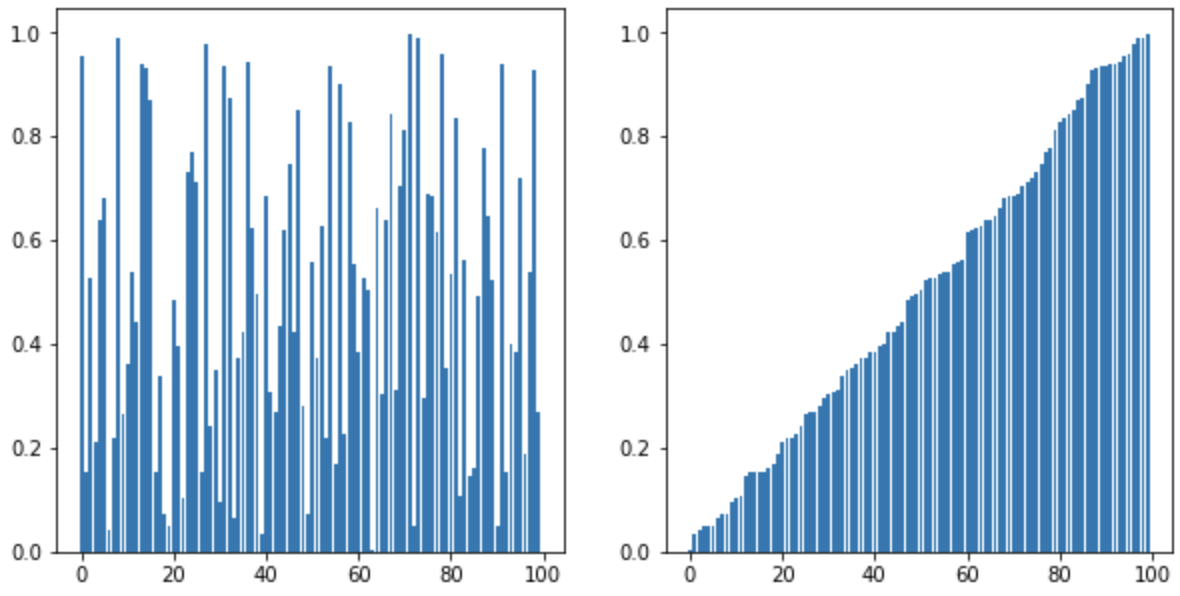
테스트
1
2
3
4
5
6
7
x = np.random.sample(500)
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.bar(range(500), x)
plt.subplot(1,2,2)
plt.bar(range(500), selection_sort(x))