Home [2021 인공지능전문가 교육과정 복습] 이진탐색트리 개념, 연산, 구현
포스트
취소

[2021 인공지능전문가 교육과정 복습] 이진탐색트리 개념, 연산, 구현

게시 2022-01-27 업데이트 2022-01-27
By Ki Beom Kim
17 분읽는 시간

이진탐색트리

정의

탐색을 위한 이진트리.

이진탐색트리 연산 시간복잡도

$O(\log{n})$

  • 트리 높이

이진트리가 이진탐색트리가 되기 위한 조건

  • 원소들이 서로 다른. 유일한 키를 갖고 있다.
  • 왼쪽 서브트리 원소들의 키는 루트보다 작다.
  • 오른쪽 서브트리 원소들의 키는 루트보다 크다.
  • 왼쪽 서브트리와 오른쪽 서브트리도 이진탐색트리 조건 만족한다.

이진탐색트리 예

Screen Shot 2022-01-25 at 11 26 57

이진탐색트리 노드

구조

(키, 값) 쌍 형태.

  • 키, 값, 왼쪽자식, 오른쪽 자식
1
2
3
4
5
6
7
8
9

# 이진탐색트리 노드 정의
# (키, 값) 쌍 

class Node : 
    def __init__(self, key, value, left=None, right=None) : 
        self.key = key 
        self.value = value 
        self.left = left
        self.right = right

이진탐색트리 탐색 연산

1. 루트에서 시작한다.

2. 탐색할 키를 루트 노드 키 값과 비교한다.

  • 키 $=$ 루트노드 키: 탐색연산 성공
  • 키 $<$ 루트노드 키: 왼쪽 서브트리로 가서 탐색 연산 수행
  • 키 $>$ 루트노드 키: 오른쪽 서브트리로 가서 탐색 연산 수행

3. 서브트리에 대해 재귀적으로 탐색 연산 반복

탐색 연산 메소드 구현

1
2
3
4
5
6
7
8
9
10

# 탐색 연산 정의
def get_item(n, k) : # 현재노드, 찾으려는 키 
    if n == None : 
        return None 
    if n.key > k : 
        return get_item(n.left, k)
    if n.key < k : 
        return get_item(n.right, k)
    else : 
        return n.value

이진탐색트리 노드 삽입 연산

정의

탐색 하다가 탐색 실패한 위치에 노드 삽입.

  • 탐색 성공 시 삽입하지 않는다. (중복값 허용 X)

키가 16인 노드를 이진탐색트리 삽입하는 예

Screen Shot 2022-01-27 at 15 32 49

과정

  • 20과 비교: 왼쪽 서브트리로 간다.
  • 10과 비교: 오른쪽 서브트리로 간다.
  • 15와 비교: 오른쪽 서브트리로 간다.
  • 15의 오른쪽 서브트리에서 탐색 실패. 탐색 실패한 자리에 16을 넣는다.

노드 삽입 연산 메소드 구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 노드삽입연산 정의

def add_item(r,n) : 
    if r.key > n.key : 
        if r.left == None : 
            r.left = n 
            return True # 삽입성공
        else : 
            return add_item(r.left, n)
    if r.key < n.key : 
        if r.right == None : 
            r.right = n 
            return True 
        else : 
            return add_item(r.right, n)
    else : # 탐색 성공한 경우 
        return False # 삽입실패

이진탐색트리 노드 삭제 연산

삭제하려는 노드 자식 수. 몇 개냐에 따라. 연산 방법. 다르다.

  • 삭제하려는 노드 자식 수 0개인 경우(단말노드)
  • 삭제하려는 노드 자식 수 1개인 경우
  • 삭제하려는 노드 자식 수 2개인 경우

연산 정의할 땐. 노드 간 관계 입체적으로 보는 게. 중요하다.

연산 수행하고 나면 항상 전체 트리의 루트R을 반환한다.

삭제하려는 노드 자식 수가 0개(단말노드)

정의

그 부모의. 자식 자리에 None을 할당한다.

1
2
3
4
5
6
7
8
9
10
11

# 단말노드 삭제연산 정의

def delete_zero(parent, node, root) : 
    if parent == None : 
        root = None 
    else : 
        if node == parent.left : 
            parent.left = None 
        else : 
            parent.right = None 
    return root

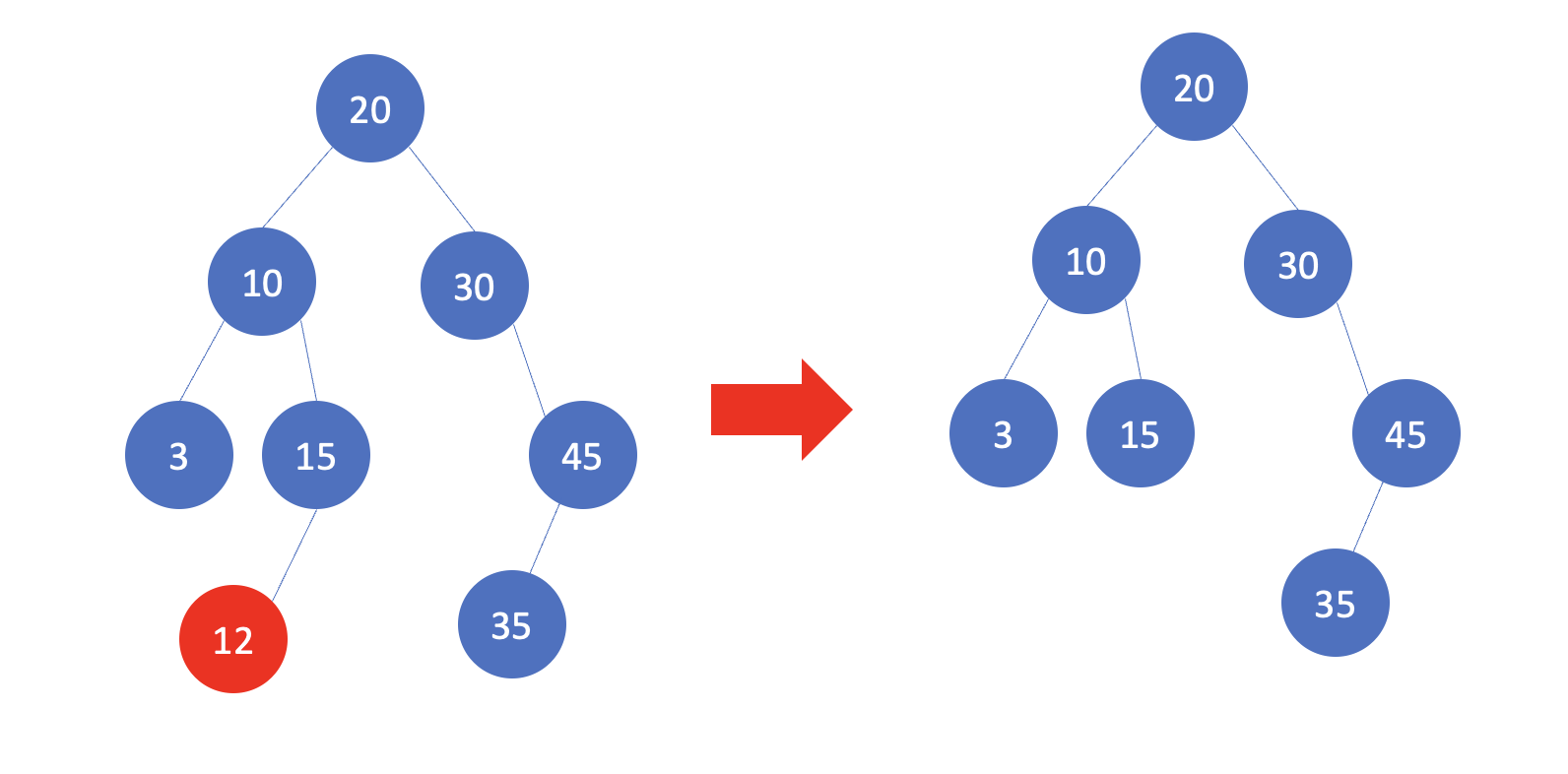
Screen Shot 2022-01-27 at 16 32 34

삭제하려는 노드 자식 수가 1개

삭제 대상 노드가 왼쪽이든 오른쪽이든. 자식 1개 있을 때.

정의

그 부모의 자식 자리에 삭제 대상 노드 외자식을 새로 할당한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 외자식 갖는 노드 삭제연산 정의 

# 노드삭제연산 정의 - 자식 수 1개인 노드 삭제 
def delete_one(parent, node, root) : 
    if node.left != None : 
        target = node.left 
    else : 
        target = node.right 

    if node == root : 
        root = target 
    else : 
        if parent.left == node : 
            parent.left = target 
        else : 
            parent.right = target 
    return root

Screen Shot 2022-01-27 at 16 33 53

삭제하려는 노드 자식 수가 2개

정의

노드의 중위순회 후속자 찾아서, 그 부모의 자식 자리에 새로 할당한다.

  • 중위순회 후속자는 ‘노드의 오른쪽 서브트리 안에서 가장 왼쪽 노드’가 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 서브트리 2개 갖는 노드 삭제연산 정의 

def delete_two(parent, node, root) : 
    target_parent = node 
    target = node.right 

    while target.left != None : 
        target_parent = target 
        target = target.left

    if (target_parent.left == target) : 
        target_parent.left = target.right
    else : 
        target_parent.right = target.right 

    node.key = target.key 
    node.value = target.value 
    return root

Screen Shot 2022-01-27 at 16 35 21

노드 삭제 연산 종합 구현

case 별 3 가지 삭제연산 종합해서 ‘삭제연산’ 구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 노드 삭제 연산 3가지 종합해서 구현 

def delete(root, key) :
    if root == None : # 공트리면 
        return None 
    #탐색
    parent = None # 현재 노드의 부모
    node = root # 현재 노드 

    while node != None and key != node.key : # 공트리 아니고. 원하는 키 찾을 때 까지 
        if (node.key > key) : 
            parent = node 
            node = node.left 
        else : 
            parent = node 
            node = node.right 

    # 원하는 키가 트리에 없으면 
    if node == None : return None 

    #-------------------삭제하려는 키에 도착했을 때--------------------------
    if node.right == None and node.left == None : # 현재 노드 단말노드면 
        root = delete_zero(parent, node, root)
    elif node.right == None or node.left == None : # 자식 1개면
        root = delete_one(parent, node, root)
    else : # 자식 2개면 
        root = delete_two(parent, node, root)
    return root

최대키, 최소키 갖는 노드 탐색 연산

  • 최대키 갖는 노드: 오른쪽 라인 타고 내려가다가 오른쪽 자식이 $None$ 인 노드.
  • 최소키 갖는 노드: 왼쪽 라인 타고 내려가다가 왼쪽 자식이 $None$ 인 노드.

최대키 갖는 노드 탐색 연산

1
2
3
4
5
6

# 최대키 갖는 노드 탐색 연산 정의

def search_max_key(node) : 
    while node != None and node.right != None : 
        node = node.right
        return node

최소키 갖는 노드 탐색 연산

1
2
3
4
5
6

# 최소키 갖는 노드 탐색 연산 정의 

def search_min_key(node) : 
    while node != None and node.left != None : 
        node = node.left 
        return node

이진탐색트리 연산 시간복잡도

연산의 범위: 삭제, 삽입, 탐색

트리 높이 만큼 시간복잡도 소요된다. $O(\log_{2}{n})$~$O(n)$

  • 최선경우(완전이진트리일 때): $O(\log_{2}{n})$
  • 최악경우(편향이진트리일 때): $O(n)$

이진탐색트리 구현

위에서 정의한 노드와 메소드를 종합해서. 이진탐색트리를 코드로 정의하겠다.

노드

1
2
3
4
5
6
7
8

# 이진탐색트리 노드 정의 

class Node : 
    def __init__(self, key, value, left=None, right=None) : 
        self.key = key 
        self.value = value 
        self.left = left 
        self.right = right

이진탐색트리 클래스

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124

# 이진탐색트리 객체 정의

class BST : 
    def __init__(self) : 
        self.root = None 
    
    # 탐색연산 
    def get(self, k) : # k=찾으려는 키
        return self.get_item(self.root, k)
    def get_item(self, n, k) : 
        if n == None : return None # 키 가진게 트리 안에 없을 때 

        # 탐색 
        if n.key > k : # 왼쪽 서브트리 
            return self.get_item(n.left, k)
        elif n.key < k : # 오른쪽 서브트리 
            return self.get_item(n.right, k)
        
        # 탐색 성공했을 때 
        else : 
            return n.value 
    
    # 삽입연산 
    def put(self, key, value) : 
        self.root = self.put_items(self.root, key, value) 
    def put_items(self, n, key, value) : 
        # 탐색 실패 했을 때 
        if n == None : return Node(key, value) 
        
        # 탐색하고 실패하면 삽입
        if n.key > key : # 왼쪽 서브트리로 고
            n.left = self.put_items(n.left, key, value)
        elif n.key < key : # 오른쪽 서브트리로 고 
            n.right = self.put_items(n.right, key, value)
        
        # 탐색 성공했을 때 
        else : 
            n.value = value 
        return n # 루트노드 반환 

    # 최솟값 삭제 연산 
    def delete_min(self) : 
        # 정의: 트리가 공 트리인 경우 
        if self.root == None : return None 
        else: self.root = self.del_min(self.root)
    
    def del_min(self, n) : 
        if n.left is None : return n.right
        n.left = self.del_min(n.left)
        return n
    
    # 특정 키 노드 삭제 연산 정의 :
    def delete(self, k) : 
        self.root = self.del_node(self.root, k)
    
    def del_node(self, n, k) : 
        # 재귀중지
        if n == None : return None 

        # 재귀호출
        if (n.key > k) : 
            # 왼쪽 서브트리 
            n.left = self.del_node(n.left, k) 
        elif (n.key < k) : 
            # 오른쪽 서브트리 
            n.right = self.del_node(n.right, k) 
        #부모의 자식 자리(왼쪽,오른쪽)에 새 n의 결과 넣는다. 

        else : #(n.key == k)
            # k노드가 단말노드 | k노드가 오른쪽 자식 1개만 있을 때 
            if (n.left== None) : return n.right
            # k노드가 왼쪽 자식 1개만 있을 때 
            elif (n.right == None) : return n.left
            else : 
                target = n # target = 현재노드
                n = self.minimum(target.right) # target 오른쪽 서브트리에서 최솟값 찾아라 
                n.right = self.del_min(target.right) # 최솟값 지운 오른쪽 서브트리를 오른쪽에 새로 할당
                n.left = target.left # 왼쪽 서브트리는 그대로 
        return n 

    # 최솟값 가진 노드 찾기. 정의. 
    def min(self) : 
        # 트리가 빈 경우
        if self.root == None : 
            return None 

        return self.minimum(self.root)
    
    def minimum(self, n) : 
        # 재귀중지 
        if n.left == None : 
            return n
        return self.minimum(n.left)
    
    # 전위순회 
    def preorder(self, n) : 
        if n != None : 
            print(n.key, end=' ') # 루트 출력
            if n.left : self.preorder(n.left) # 왼쪽 서브트리 전위순회
            if n.right : self.preorder(n.right) # 오른쪽 서브트리 전위순회 
    
    # 중위순회 
    def inorder(self, n) : 
        if n.left : self.inorder(n.left) # 왼쪽 서브트리 중위순회 
        print(n.key, end=' ')
        if n.right : self.inorder(n.right) # 오른쪽 서브트리 중위순회 

    # 후위순회 
    def postorder(self, n) : 
        if n.left : self.postorder(n.left) # 왼쪽 서브트리 후위순회 
        if n.right : self.postorder(n.right) # 오른쪽 서브트리 후위순회 
        print(n.key, end=' ')

    # 레벨순회 
    def levelorder(self, n) : 
        que = []
        que.append(n) 
        while len(que) != 0 : # 큐가 빌 때 까지 
            e = que.pop(0)
            print(e.key, end=' ')
            if e.left != None : 
                que.append(e.left)
            if e.right != None : 
                que.append(e.right)
  • 대부분 연산을 함수 재귀호출 사용해 구현했다.

함수 재귀호출 사용했을 때. 메소드가 어떻게 동작하는 지 깔끔한 이해가 어려울 땐. 종이에 직접 재귀호출 과정 기록하면서 따라가니 이해에 큰 도움 되었다.

이진탐색트리 객체가 잘 동작하는 지 테스트

데이터 삽입

1
2
3
4
5
6
7
8
9
10
11

# 이진탐색트리 테스트 
# 빈 이진탐색트리에 노드 삽입

if __name__ is '__main__' : 
    t = BST() # 이진탐색트리
    t.put(500, 'apple');t.put(600, 'banana')
    t.put(200, 'melon');t.put(100, 'orange')
    t.put(400, 'lime');t.put(250, 'kiwi')
    t.put(150, 'grape');t.put(800, 'peach')
    t.put(700, 'cherry');t.put(50, 'pear')
    t.put(350, 'lemon');t.put(10, 'plum')

위 삽입 결과를 직관적으로 시각화 하면 아래와 같을 것이다.

Screen Shot 2022-01-27 at 17 03 47

전위순회

1
2

# 전위순회
print('전위순회:\t', end=' ');t.preorder(t.root)

전위순회: 500 200 100 50 10 150 400 250 350 600 800 700

중위순회

1
2

# 중위순회 
print(f'중위순회:\t', end=' ');t.inorder(t.root)

중위순회: 10 50 100 150 200 250 350 400 500 600 700 800

탐색연산: 250

1
2

# 탐색연산 : 250 
print('\n250: ', t.get(250))

250: kiwi

삭제연산

1
2

# 삭제연산 
t.delete(200)

삭제 후 전위순회

1
2
3
4

print('삭제후:\t', end=' ')

# 전위순회 
print('전위순회:\t', end=' ');t.preorder(t.root)

삭제후: 전위순회: 500 250 100 50 10 150 400 350 600 800 700

삭제 후 중위순회

1
2
3

# 삭제 후 중위순회 
print('\n중위순회:\t', end=' ')
t.inorder(t.root)

중위순회: 10 50 100 150 250 350 400 500 600 700 800

최솟값 삭제: 10

1
2

# 최솟값 삭제 
t.delete_min()

최솟값 삭제 후 중위순회

1
2

# 최솟값 삭제 후 중위순회
t.inorder(t.root)

50 100 150 250 350 400 500 600 700 800

최솟값 삭제 후 후위순회

1
2

# 최솟값 삭제 후 후위순회
t.postorder(t.root)

50 150 100 350 400 250 700 800 600 500

최솟값 삭제 후 레벨순회

1
2

# 최솟값 삭제 후 레벨순회 
t.levelorder(t.root)

500 250 600 100 400 800 50 150 350 700

Data Science, python, data structure
data structure computer science study data science python
최근 업데이트
바로가기

[Keras/딥러닝 공부] 신경망 기본 구성, 이진분류, 다중분류, 회귀문제

[2021 인공지능전문가 교육과정 복습] AVL 트리 개념, 연산, 구현