‘프로그래머가 알아야 할 알고리즘 40’(임란 아마드 지음, 길벗 출판사) 을 통해 3가지 문제 해결 전략을 공부. 복습하고나서, 그 내용을 내 언어로 바꾸어 기록한다.
알고리듬 설계에 적용할, 문제해결 전략
- 분할 정복 전략(divide and conquer)
- 동적 계획법
- 탐욕 알고리듬
1. 분할 정복 전략
정의
문제를 작은 문제로 쪼개어 각개격파 한 뒤 결과물을 모으는 문제해결 방식.
2. 동적 계획법
‘기억하며 풀기’
정의
문제를 하위 문제 여러 개로 나누어, ‘최적의 방법으로’ 해결한 뒤 결과물 모으는, 분할 정복 전략.
메모이제이션 통해서 하위 문제들을 최적 방법으로 해결한다.
- 메모이제이션: 하위 문제 연산 결과를 저장하고 있다가 중복되는 문제 등장하면 연산없이 곧바로 해결하기.
3. 탐욕 알고리듬(Greedy algorithm)
현재상황에서 최선의 선택, 항상 내리기.
정의
알고리듬 오버헤드 최소화 하는 문제 해결 전략.
- 알고리듬 오버헤드: 알고리듬 실행에 소요되는 부가적인 시간, 메모리 등 자원.
장점
빠르다.
단점
찾은 해가 전역 최적해라는 보장이 없다.
$\Rightarrow$ 근사 알고리듬의 일종이다.
탐욕 알고리듬 활용 사례: 외판원 문제
규칙
- 모든 도시를 한번씩 만 방문할 수 있다.
- 여정 끝에 시작한 도시로 다시 돌아와야 한다.
- 도시 간 거리는 모두 알려져 있다.
*도시가 $n$ 개 있으면, 가능한 여정은 $(n-1)!$ 개 이다.
문제 기능적 요구사항 파악
- 입력: $n$ 개 도시 리스트, $n$ 개 도시 서로 간 거리
- 출력: 여정거리 최소 되는 투어 경로
문제 해결 전략 1: 무차별 대입 전략
무차별 대입(brute-force strategy): 무식하게 직접 하나하나 노가다 해서 원하는 출력 찾는 전략.
비밀번호 4자리가 있으면, 가능한 모든 수를 모든 자리에 일일이 넣어보면서 정답 찾는 전략이다.
경우의 수가 적을 때는 오히려 정확한 답 찾는 데 효과적이다.
하지만 경우의 수가 많아지면 알고리즘 시간복잡도가 기하급수적으로 증가하기 때문에 좋은 전략이 못 된다.
무차별 대입 전략 구현해서 문제 해결하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 무차별 대입 전략 구현하기
import random
from itertools import permutations
# permuations: 리스트 받아서 가능한 순열 모두 생성한다.
alltours = permutations
# distance_tour: 총 여정거리 계산하는 함수. sum 함수 안에서도 리스트 축약식처럼 for문 사용 가능하다는 점 눈여겨 봐 두자.
def distance_tour(atour) : return sum(distance_points(atour[i-1], atour[i]) for i in range(len(atour)))
# complex 는 a+bj 꼴 복소수 생성하는 클래스다. a: 실수부, bj는 허수부. 복소수 1개는 벡터와 같다. 각 도시를 2차원 벡터공간 상의 벡터로 표현하기 위해 사용한다.
acity = complex
# first 벡터와 second 벡터 사이 유클리드 거리 계산하는 함수(도시 간 거리 계산).
def distance_points(first, second) : return abs(first-second)
# 가로 500, 세로 300인 2차원 벡터공간에 무작위로 벡터 생성한다. 각 벡터는 도시 상징한다.
def generate_cities(number_of_cities) :
seed = 10
width = 500
height = 300
random.seed((number_of_cities, seed))
return frozenset(
# x 축에서 랜덤하게 좌표 생성
acity(random.randint(1, width),
# y 축에서 랜덤하게 좌표 생성
random.randint(1, height))
# 도시 수 만큼 반복해서 벡터 생성(중복 frozenset으로 제거)
for c in range(number_of_cities))
무차별 대입 함수 구현. 총 여정거리 최소인 투어 경로 찾아서 산출한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import matplotlib.pyplot as plt
# 무차별 대입 함수 구현 : 여러 투어 후보군 중 최소 투어 찾아서 출력
def brute_force(cities) : return shortest_tour(alltours(cities))
# 총 거리 최소인 투어 반환
def shortest_tour(tours) : return min(tours , key = distance_tour)
def visualize_tour(tour) :
# 투어 크기 일정 이상 커지면, 전체 이미지 크기 조정
if len(tour) > 1000 : plt.figure(figsize=(15,10))
# 여정 시작점
start = tour[0:1]
# 경로 시각화. 여정 마지막점 == 시작점 되기 위해 tour + start 한다.
visualize_segment(tour+start)
# 여정 시작점은 빨간색으로 칠해서 돋보이게 해라
visualize_segment(start, 'rD')
# 리스트 받아서 2차원 벡터공간에 (x좌표, y좌표) 찍어 시각화 하는 함수.
def visualize_segment(segment, style='bo-') :
plt.plot([x(c) for c in segment], [y(c) for c in segment], style)
# x축, y축 이미지에서 제거
plt.axis('scaled')
plt.axis('off')
# 복소수 입력으로 받아서 실수부만 추출하는 함수. 벡터의 x축 좌표와 같다.
def x(c): return c.real
# 복소수 입력으로 받아서 허수부만 추출하는 함수. 벡터의 y축 좌표와 같다.
def y(c) : return c.imag
문제 해결
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 리스트 각 요소 갯수 세서 딕셔너리 반환해준다
from collections import Counter
import time
def tsp(algorithm, cities) :
t0 = time.perf_counter() # 알고리듬 시작시간
tour = algorithm(cities) # 거리 최소인 투어(여정 경로) 산출.
t1 = time.perf_counter() # 알고리듬 종료시간
# 결과 경로가 모든 도시 한번씩만 방문했는지 검증
assert Counter(tour) == Counter(cities)
# 결과 경로 2차원 벡터공간 상에 시각화
visualize_tour(tour)
# 결과
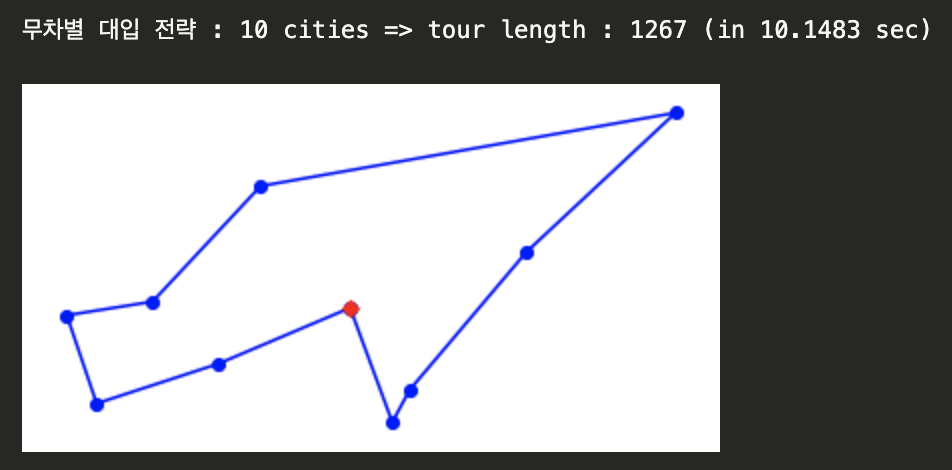
print(f'무차별 대입 전략 : {len(cities)} cities => tour length : {round(distance_tour(tour))} (in {round(t1-t0,4)} sec)')
# 10개 도시에 대해 총 여정거리 최소인 경로 찾기
tsp(brute_force, generate_cities(10))
문제 해결 전략 2: 탐욕 알고리듬(그리디 알고리듬)
무차별 대입 전략은 방문해야 할 도시 수가 적을 때는 정확한 정답 찾는 유용한 문제해결 전략이다.
하지만 방문해야 할 도시 수가 많아지면 많아질 수록, 가능한 후보 경로 수가 기하급수적으로 많아진다($n-1!$). 이 경우에 무차별 대입 전략 사용할 경우 말 그대로 억겁의 시간이 걸릴 수 있다.
곧, 방문할 도시 수가 많은 경우엔 무차별 대입 전략은 사용하기 부적절하다.
무차별 대입전략을 적용하기 어려운 경우에 대해(도시 수를 크게 늘려서),
탐욕 알고리듬을 적용해서 총 여정 경로 최소가 되는 투어 경로 찾아보자.
탐욕 알고리듬
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 그리디 알고리즘
def greedy_algorithm(cities, start=None) :
c = start or first(cities) # 여정 시작 도시
# 여정
tour = [c]
# 방문 안 한 곳
unvisited = set(cities - {c})
while unvisited : # 방문 안 한 곳이 남아 있는 한
c = nearest_neighbor(c, unvisited) # 가장 가까운 도시
tour.append(c) # 여정 생성
unvisited = unvisited - {c} # 방문안 한 곳 리스트에서 이번에 방문한 도시 제거
return tour
def first(cities) : return next(iter(cities))
def nearest_neighbor(start, cities) : return min(cities, key= lambda c : distance_point(c, start))
탐욕 알고리듬으로 문제해결 실행; 5000개 도시 있을 때 최단 경로 찾기
1
2
# 도시 수 : 5000개
tsp(greedy_algorithm, generate_cities(5000))
무차별 대입 전략 : 4921 cities => tour length : 24055 (in 2.7062 sec)

매 순간 최적 선택지(거리 가장 가까운 도시) 선택하는 탐욕 알고리듬은 단 2.7초 만에 최단 투어 경로 찾아냈다.
탐욕 알고리듬이 더 많은 도시 개수에도 불구하고, 도시 10개 밖에 안 되는데 10초 넘게 걸렸던 무차별 대입전략 보다 약 5배 빨랐다.
다만, 탐욕 알고리듬은 근사 알고리듬이기 때문에, 이 알고리듬이 찾은 정답은 전역 최적해가 아닐 수 있다. 즉, 거시적 관점에서 전체 도시와 경로를 보면 탐욕 알고리듬이 찾은 경로가 최단 경로가 아닐 수 있다.
