엔트로피
정의
확률분포에서 나온 표본 1개가 특정 표본인지 추려내기 위해 필요한 평균 질문 갯수(정보량)
- 분포의 불확실성
- 분포에서 새롭게 얻을 수 있는 정보의 양 (=놀람의 정도)
- 분포의 분산 정도
- 엔트로피 단위 : 비트
표기
- H
- 수학적 정의는 확률변수를 입력으로 받는 범함수다.
이산확률변수
$H[Y] = -\sum_{i=1}^{k} p(y_{k})\log_{2}{p(y_{k})}$
연속확률변수
$H[Y] = -\int p(y)\log_{2} p(y) dy$
1
2
3
4
5
6
7
8
9
10
11
12
xx = np.linspace(0,1,10000)
ent_values = []
for p in xx :
if p == 0 or p == 1 :
ent_values.append(0)
else :
ent_value = -(1-p)*np.log2(1-p)-p*np.log2(p)
ent_values.append(ent_value)
plt.plot(xx, ent_values)
plt.title('엔트로피 $H[Y]$')
plt.show()

사이파이 엔트로피 계산 코드
1
sp.stats.entropy(p, base=2)
p 는 엔트로피를 계산할 확률분포다.
엔트로피의 성질
- 엔트로피 최솟값은 0 이다.
분포 분산정도가 극단적으로 낮은 경우, 엔트로피 값이 0 나올 수 있다.
- 분포 분산 정도와 엔트로피값 크기는 정비례 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
x1 = [1/8, 1/8, 1/4, 1/2]
x2 = [1,0,0,0]
x3 = [1/4]*4
plt.figure(figsize=(9,3))
plt.subplot(131)
plt.bar([0,1,2,3],x1)
plt.xticks([0,1,2,3], ['Y=0', 'Y=1', 'Y=2', 'Y=3'])
plt.title('$H[Y] = 1.75$')
plt.ylim(0,1.1)
plt.subplot(132)
plt.bar([0,1,2,3],x2)
plt.xticks([0,1,2,3], ['Y=0', 'Y=1', 'Y=2', 'Y=3'])
plt.title('H[Y] = 0')
plt.ylim(0,1.1)
plt.subplot(133)
plt.bar([0,1,2,3], x3)
plt.xticks([0,1,2,3], ['Y=0', 'Y=1', 'Y=2', 'Y=3'])
plt.title('$H[Y] = 2$')
plt.ylim(0,1.1)
plt.suptitle('분산정도가 작을 수록 엔트로피가 작아진다',y=1.04)
plt.tight_layout()
plt.show()

위 그림에서
두번째 분포는 표본 얻었을 때 Y=0이 나올 가능성이 100% 다. 이 분포에서 앞으로 어떤 정보를 얻어도 놀랍지 않을 것이다. 왜냐하면 불 보듯 뻔하게 1이 나올 것이기 때문이다. 따라서 두번째 분포는 새롭게 얻게 될 정보량(엔트로피)가 0 이다.
또한 두번째 분포는 분산 정도 또한 극단적으로 낮음을 볼 수 있다. 분산 정도가 작으면 분포의 엔트로피값도 작다.
한편
세번째 분포는 범줏값 0~3이 나올 확률이 모두 같다. 따라서 내가 이 분포에서 표본을 얻으려 할 경우, 뭐가 나올지 전혀 알 수 없다. 따라서 이 분포에서 데이터를 1개 얻을 경우, 그 데이터는 귀중한 가치를 지닌 ‘정보’ 가 된다. 이후에 얻는 데이터 하나하나도 정보가치가 충분할 것이다. 따라서 이 분포는 새롭게 얻게 될 정보량이 많은 분포라고 생각할 수 있다. 엔트로피는 이런 경우 가장 커진다.
또 세번째 분포 분산정도 또한 매우 높음을 볼 수 있다. 분산 정도가 클 수록 분포의 엔트로피 값도 크다.
가변길이 인코딩과 고정길이 인코딩
가변길이 인코딩
- 인코딩 : 표본 1개에 대한 질문-응답 결과와 같았다.
- 가변길이 인코딩 : 확률분포 확률값들에 따라 질문하는, 가장 효율적인 질문 전략
가변길이 인코딩 예)
$p = [0.5, 0.25, 0.125, 0.125]$ 라는 분포가 있다고 가정해보자.

이 분포를 갖는 확률변수에서 뭔진 모르겠지만 어떤 표본 하나가 나온다고 하자.
이 표본이 뭔지 어떻게 추려낼 것인가?
질문을 던지면 된다.
예를 들어 ‘나온 표본은 A’인가? , ‘B인가?’ 등등으로 물을 수 있다. 하나의 질문에 대해 YES 나 NO로 대답해가면서 이번에 나온 표본이 뭔지 추릴 수 있다.
가변길이 인코딩은 이 ‘질문 방식’으로 생각할 수 있다.
가변길이 인코딩에서는 기본적으로 각 표본마다 할당된 확률값에 기초해 질문을 던진다.
예를 들어 A가 0.5로 가장 확률이 높다. 표본 하나를 얻었을 때 그게 A일 확률이 가장 높다. 그러면 첫 질문으로 A인가? 아니면 BCD인가? 이렇게 질문을 던진다.
그리고 만약 A이면 A를 추려낸 것이고, A가 아니면 다시 두번째로 확률높은 B인가? 를 질문한다.
이런식으로 C,D까지 추려낼 수 있다. 그 후 각 질문에 대한 답변에 기초해 각 문자를 이진수로 인코딩할 수 있다.
예를 들어 A는 첫 질문에서 YES라고 답한 후 추려졌다.
YES = 0, NO = 1 로 생각하면, A는 곧 0으로 인코딩 된다.
나머지 알파벳도 마찬가지다.

A는 0으로 인코딩 되었는데, 한 자리다. 이는 비트 하나, 그러니까 질문 1개 를 나타낸다.
D는 111로 인코딩 되었는데, 세 자리다. 이는 비트 셋, 그러니까 질문 3개를 나타낸다.
- 참고) 한 글자에 인코딩 된 이진수는 다른 글자에 인코딩 된 이진수의 접두어가 될 수 없다.
고정길이 인코딩
- 모든 표본이 균등분포에서 나왔다고 전제한다.
- 어떤 표본이 더 나오고, 덜 나오고 없다.
모든 표본이 나올 가능성이 같으므로, 어떤 표본을 먼저 추려내고, 늦게 추려내고 할 수 없다. 따라서 다른 방법으로 추려내야 한다.
이때 표본을 추려내는 최적의 질문전략은 다음과 같다.
‘ABCD’ 이면, 절반/절반으로 나누어 표본을 추려내고, 다시 거기서 절반/절반을 나누어 표본을 추려낸다.
‘AB’, ‘CD’
‘A’, ‘B’, ‘C’, ‘D’ 이렇게 나누는 식이다.

위 그림과 같다.
이렇게 표본을 추려내면 모든 표본에 대해 질문횟수가 같다.
YES = 0, NO = 1로 두고, 각 알파벳을 질문 결과에 따라 인코딩 하면
A = 00
B = 01
C = 10
D = 11
이렇게 인코딩할 수 있는데, 이게 고정길이 인코딩 방식이다.
엔트로피 - 가변길이 인코딩 사이 관계
- 엔트로피 값 = 가변길이 인코딩 했을 때 표본 1개당 평균 정보량
예)
어떤 문서가 있다. 이 문서는 A,B,C,D,E,F,G,H 로 구성되어 있다. 각 알파벳이 등장할 확률은 다음과 같다.
$P = [1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, 1/64]$
이 문서 알파벳들을 전부 가변길이 인코딩 할 때, 알파벳 1개 당 평균 비트 수는?
답)
먼저, 이 문서는 K = 8 인 카테고리 확률변수에서 나온 표본들을 모아놓은 것과 같다.
예컨대 문서가
‘AAAAABAAAACDAAAADABBBCCBBABBCABDABADADACBABACBADAABAACAADAABDCDCCABADCAACABABBAAAACDABBBDABCAAADDBBAABAAACAADADBCACBADBABAAABAAAABACABBBABAABCBABAAABACAACAACAAADABBBAAABDCDACDAAAADAAAABDAABABCDABBBDAA’
이런 식 이라면, 이건 K = 8인 카테고리 확률변수를 200번 시뮬레이션 해서 얻어낸 데이터 집합이다.
이 문서가 결국 카테고리확률변수의 표본이라는 게 핵심이다.
앞에서 비트 수는 질문갯수와 같았다.
가변길이 인코딩 했을 때 알파벳 1개 당 평균 비트 수는 :
확률변수 확률분포에 따라 질문 던지고 각 표본 추려냈을 때, 표본 1개 당 평균 질문 갯수와 같다.


확률변수의 확률분포에 따라 질문을 던지고 각 표본값을 추려내 보았다.
그리고 각 질문에 대한 대답에 따라 각 표본을 이진수 인코딩 할 수 있었다.
A = 0
B = 10
C = 110
D = 1110
E = 111100
F = 111101
G = 111110
H = 111111
각 표본 1개 당 평균 비트 수는 각 확률분포값에 질문 갯수를 곱해서 가중합 한 것과 같다.
1
(1/2*1)+(1/4*2)+(1/8*3)+(1/16*4)+(1/64*6)*4
표본 1개 당 평균 비트 수(질문 갯수, 정보량) : 2.0
이 나온다.
한편
“엔트로피-가변길이 인코딩 간 관계”에 의해서 표본이 나온 분포의 엔트로피 값은 가변길이 인코딩 했을 때 표본 1개 당 평균 정보량(비트 수, 질문 갯수) 와 같았다.
따라서 A,B,C,… 표본이 나온 카테고리 확률분포의 엔트로피 값을 구하면, 표본 1개 당 평균 정보량을 구할 수 있다.
1
2
3
4
5
6
7
8
9
10
p = [1/2, 1/4, 1/8, 1/16] + [1/64]*4
sns.barplot(np.arange(1,9), p)
plt.title('문서 : $k=8$ 인 카테고리 확률분포')
avg_info = sp.stats.entropy(p, base=2)
plt.xlabel('$k$')
plt.xticks(np.arange(8), ['A','B','C','D','E','F','G','H'])
plt.show()
print(f'표본 1개 당 평균 정보량(=비트 수) : {avg_info}')
print(f'k=8인 카테고리 확률분포의 엔트로피 : {avg_info}')

k=8인 카테고리 확률분포의 엔트로피 : 2.0
표본 1개 당 평균 정보량(=비트 수) : 2.0
이다. 확률분포의 엔트로피값과 표본 1개당 평균 질문갯수가 같음을 재확인할 수 있었다.
지니불순도
- 엔트로피 대용으로 쓸 수 있는 값
- 지니불순도*2 는 엔트로피 값에 근사한다.
$G[Y] = \sum_{k=1}^{k} P(y_{k})(1-P(y_{k}))$
엔트로피와 지니불순도 비교
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
p = np.linspace(0.0001, 1-0.0001, 10000)
G = [p*(1-p)+(1-p)*p for p in p]
H = [-p*np.log2(p)-(1-p)*np.log2(1-p) for p in p]
G2 = [(p*(1-p)+(1-p)*p)*2 for p in p]
plt.subplot(121)
plt.plot(p, G, label='지니불순도')
plt.plot(p, H, label='엔트로피')
plt.title('지니불순도와 엔트로피')
plt.xlabel('$P(Y=1)$')
plt.legend()
plt.subplot(122)
plt.plot(p, G2, label='지니불순도 값 * 2')
plt.plot(p, H, label='엔트로피')
plt.title('지니불순도*2 와 엔트로피')
plt.xlabel('$P(Y=1)$')
plt.legend()
plt.suptitle('엔트로피와 지니불순도 비교', y=1.007)
plt.tight_layout()
plt.show()

지니불순도 *2 를 하면 엔트로피값에 근사하는 것을 볼 수 있었다.
결합엔트로피
- 결합확률분포의 엔트로피 (벡터 분포의 엔트로피)
- 일반적인 엔트로피와 성질이 같다. 분포 분산 정도가 작을 때 엔트로피 값 작아지고, 분산 정도가 클 때 엔트로피 값 커진다. 최솟값은 0이다.
이산확률변수 X,Y
$H[X,Y] = -\sum_{i=1}^{K_{X}} \sum_{j=1}^{K_{Y}} p(x_{i}, y_{j})\log_{2}{p(x_{i}, y_{j})}$
연속확률변수 X,Y
$H[X,Y] = -\int_{x} \int_{y} p(x,y)\log_{2}{p(x,y)}dxdy$
조건부엔트로피
- 확률변수 X로 확률변수 Y를 예측할 수 있는 정도 나타낸다
- X,Y 사이 상관관계, 독립 정도를 나타낸다.
- $X = x_{i}$ 일 때 $Y$ 확률변수 조건부엔트로피를 $X$ 주변확률분포값을 가중치 삼아 가중합 한 것이다.
1. $X = x_{i}$ 일 때 Y 확률변수 조건부엔트로피
이산확률변수
$H[Y\vert X = x_{i}] = -\sum_{j=1}^{K_{Y}}p(y_{i}\vert x_{i})\log_{2}{p(y_{i} \vert x_{i})}$
연속확률변수
$H[Y\vert X = x] = -\int_{y}p(y\vert x)\log_{2}{p(y\vert x)}dx$
2. 조건부엔트로피
이산확률변수 X,Y
$H[Y\vert X] = \sum_{i=1}^{K_{X}} p(x_{i})H[Y\vert X=x_{i}]$
연속확률변수 X,Y
$H[Y\vert X] = \int_{x} p(x)H[Y\vert X = x]dx$
X로 Y예측가능한 정도와 조건부엔트로피는 반대로 움직인다
- 확률변수 X로 확률변수 Y 예측가능한 정도가 클 수록 조건부엔트로피 감소
- 확률변수 X로 확률변수 Y 예측가능한 정도가 작을 수록 조건부엔트로피 증가
조건부엔트로피 계산함수
1
2
3
4
5
6
def cond_entropy(df) :
cond_p1 = df.values[0]/df.values[0].sum()
cond_p2 = df.values[1]/df.values[1].sum()
ent1 = sp.stats.entropy(cond_p1, base=2)
ent2 = sp.stats.entropy(cond_p2, base=2)
return (df.values[0].sum()/df.values.sum())*ent1 + (df.values[1].sum()/df.values.sum())*ent2
조건부엔트로피 활용 예
데이터사이언스스쿨 연습문제 10.2.1
문) 사이킷런 패키지 붓꽃 데이터에서, 꽃받침 길이와 꽃받침 폭 중 어떤 데이터가 붓꽃 종 분류(예측)에 더 도움이 되는가?
꽃받침 길이, 꽃받침 폭 데이터의 최솟값과 최댓값 사이를 0.05 간격 구간으로 나누어, 각각의 값을 분류 기준값으로 삼았을 때 조건부엔트로피값이 어떻게 변하는지 그래프로 그려서 설명해라.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from sklearn.datasets import load_iris
data = load_iris()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['species'] = data.target
def plot_cond_entropy(df, name) :
len_min = np.min(df[name].values)
len_max = np.max(df[name].values)
xx = np.arange(len_min, len_max+0.05, 0.05)
entropies = []
for i in xx :
df['X1'] = df[name] > i
pivot_table = df.groupby(['X1', 'species']).size().unstack().fillna(0)
cond_p1 = pivot_table.values[0]/pivot_table.values[0].sum()
cond_p2 = pivot_table.values[1]/pivot_table.values[1].sum()
ent1 = sp.stats.entropy(cond_p1, base=2)
ent2 = sp.stats.entropy(cond_p2, base=2)
cond_entropy = (pivot_table.values[0].sum()/pivot_table.values.sum())*ent1 + (pivot_table.values[1].sum()/pivot_table.values.sum())*ent2
entropies.append(cond_entropy)
ind = entropies.index(np.min(entropies))
optimized_value = np.round(xx[ind],2) ; min_ent = np.round(np.min(entropies),2)
print(f'최적해 : {optimized_value}, 최저 조건부엔트로피 : {min_ent}')
plt.plot(xx, entropies)
plt.scatter(optimized_value, min_ent, 30, 'r')
plt.title(f'{name} 기준값 별 조건부엔트로피 변화')
plt.xlabel('꽃받침 길이 기준값')
plt.ylabel('조건부엔트로피')
plt.show()
1. 꽃받침 길이를 기준값으로 삼았을 때
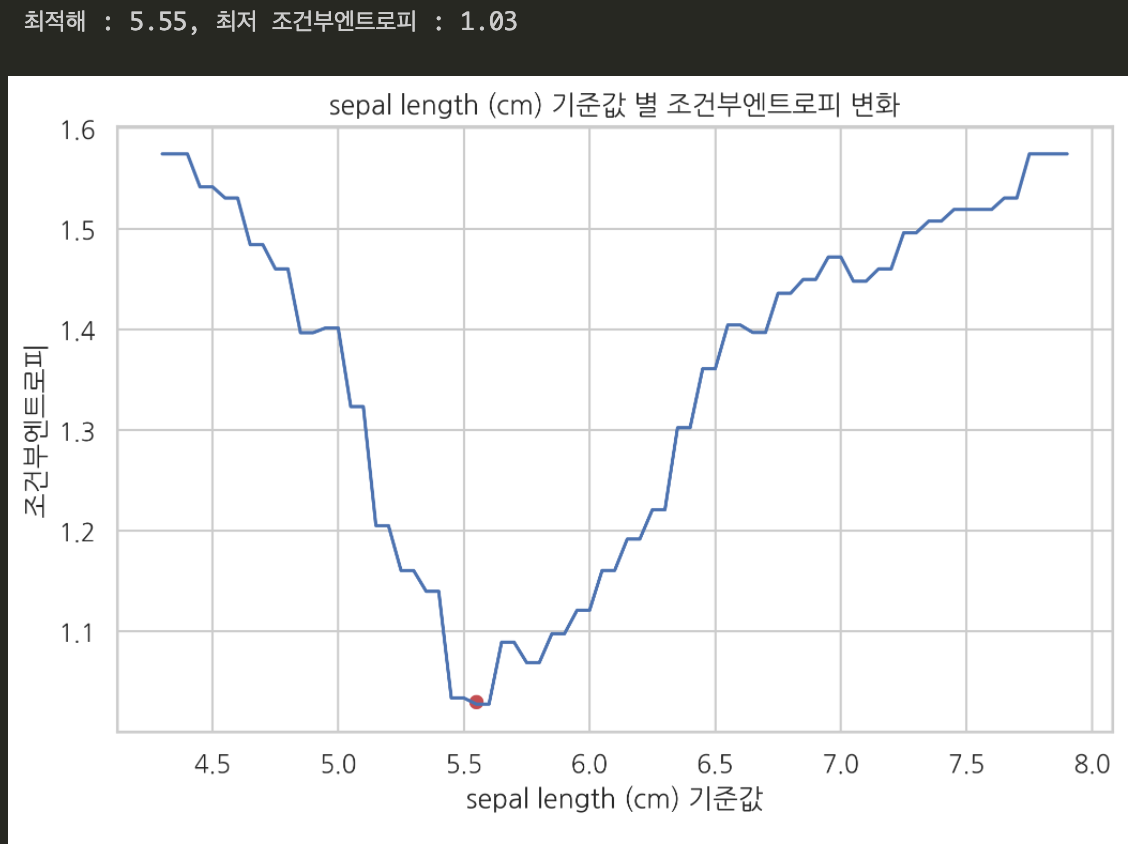
조건부엔트로피가 최소가 되는 꽃받침길이 기준값(최적해) 는 5.55 였다. 이때의 최저 조건부엔트로피값은 1.03 이었다.
2. 꽃받침 폭을 기준값으로 삼았을 때
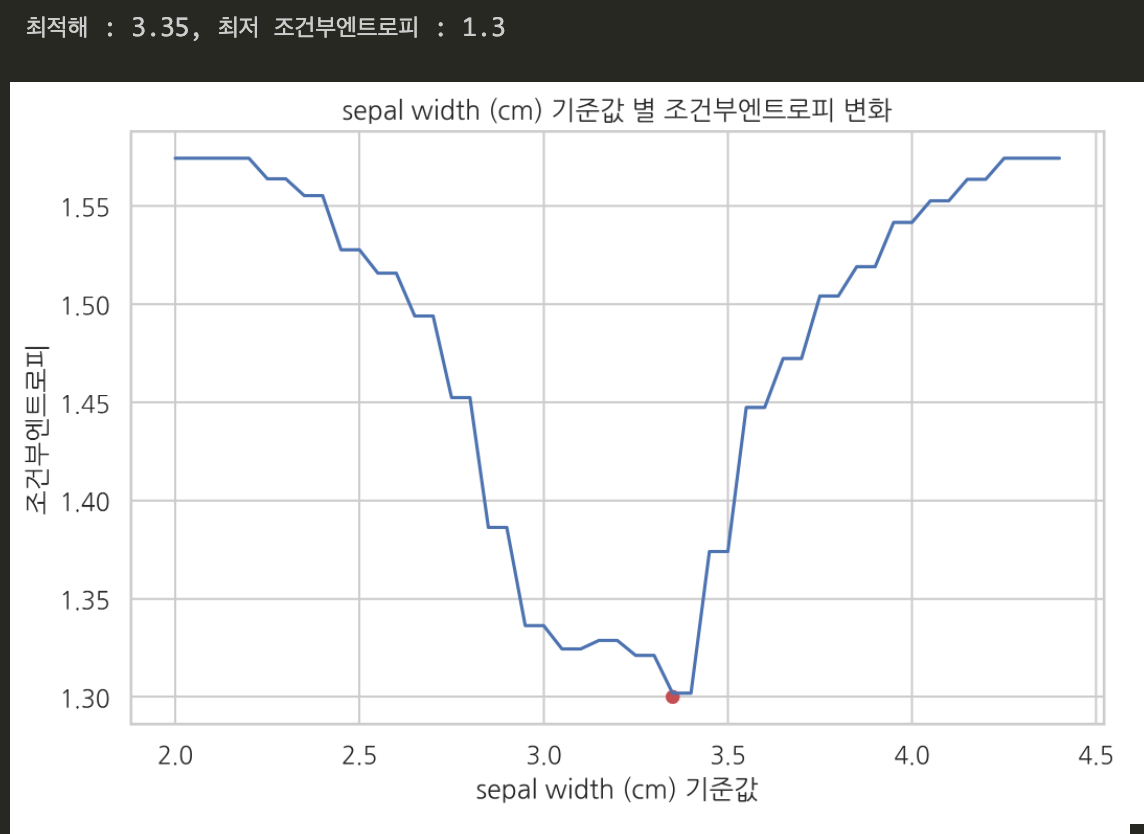
조건부엔트로피가 최소가 되는 꽃받침 폭 기준값(최적해) 는 3.35 였다. 이때의 최저 조건부엔트로피값은 1.3 이었다.
3. 결론
꽃받침 길이를 기준값으로 썼을 때는 꽃받침 길이가 5.55cm 를 넘느냐/넘지 않느냐를 기준으로 종 분류가 가능했다.
꽃받침 폭을 기준값으로 썼을 때는 꽃받침 폭이 3.35를 넘느냐/넘지 않느냐를 기준으로 종 분류가 가능했다.
그리고 각 기준값에서, 조건부엔트로피값은 각각 1.03, 1.3 이었다.
조건부엔트로피 값은 ‘X 확률변수로 Y 확률변수를 예측할 수 있는정도’를 의미했다. 조건부엔트로피 값이 작을수록, X 확률변수로 Y 확률변수를 더 잘 예측할 수 있다. 꽃받침 길이를 기준값으로 삼았을 때 조건부엔트로피가 더 작았다. 꽃받침 길이가 꽃받침 폭 보다 ‘이 꽃의 종이 뭔지’ 더 잘 분류할 수 있는 특징값이라는 뜻이다.
$\Rightarrow$ ‘꽃받침 길이’가 ‘꽃받침 폭’ 보다 종 분류에 더 도움되는 특징값이다!
크로스엔트로피 (교차엔트로피)
https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
위 블로그의 크로스엔트로피 설명을 통해 이 개념을 확실히 이해할 수 있었다.
도움을 받아 내가 이해한 내용을 다시 정리하면,
크로스엔트로피란 다음과 같다.
크로스엔트로피 정의 : “P 확률분포에서 나오는 표본이 뭔지 알아맞히기 위해, 질문전략으로 Q분포를 썼을 때 평균 질문 갯수”
정의 설명)
p 확률분포가 다음과 같다고 가정하자.
$p = [0.5, 0.25, 0.125, 0.125]$
p는 A,B,C,D 가 나오는 카테고리확률변수다.

여기서 어떤 임의의 표본이 하나 나올 때 마다, 내가 얻은 표본이 뭔지 추려내기 위한 질문을 해보자.
가변길이 인코딩 파트에 기록했던 것 처럼, 가장 효율적 방식으로 P에서 나온 표본을 추려내기 위한 질문을 하면 다음과 같다.

이 경우 각 표본당 평균 질문 갯수를 구하면 1.75다.
이 값은 p 분포의 엔트로피($H[p]$)를 구하면 얻을 수 있다.
1
sp.stats.entropy(p, base=2)
한편 p분포 이외에도 q 분포가 있다고 하자.
q 분포는 다음과 같다.
$q = [0.25, 0.25, 0.25, 0.25]$
q분포는 확률질량값이 모두 똑같다. 따라서 아래 처럼 질문할 수 있다.

이때 표본 1개 당 평균 질문 갯수는 2다.
그럼 이제 q분포에 따른 질문전략(모든 표본에 동일한 수의 질문 던지기)을 p분포 표본들을 추려내기 위해 사용해보자.
p 분포에서 나오는 표본은 A,B,C,D 였다.
이걸 q 질문 전략을 써서 추려내면 표본 1개 당 평균 질문 갯수는 2다.
이 값 2가 ‘교차엔트로피(크로스엔트로피)’ 값이다.
“p확률분포에서 나온 표본을 q분포에 따라 추려낼 때, p분포 표본 1개 당 평균 질문 갯수”
p에서 나온 표본에 대해 최적의 질문전략(위 경우 p)를 썼을 때, 크로스엔트로피값은 최소화된다.
분포 q(새로운 질문전략)가 분포 p(최적 질문전략)와 비슷해질 수록 크로스엔트로피값은 줄어든다.
크로스엔트로피 식
p, q가 이산확률분포
$H[p,q] = -\sum_{k=1}^{K} p(y_{k})\log_{2}{q(y_{k})}$
p, q가 연속확률분포
$H[p,q] = -\int_{y}p(y)\log_{2}{q(y)}dy$
또는 (이게 더 편해서 따로 기록)
$H[p,q] = KL(p\Vert q) + H[p]$
- 범함수 입력으로 확률변수가 아닌 확률분포함수 p,q가 들어간다.
- $H[p]$ 값은 분포 p 표본 1개당 평균 질문갯수로, 고정된 값이다.
- KL 값은 q, p 분포 모양이 다른 정도다.
1
2
3
4
5
6
7
# 크로스엔트로피
def calc_cross_entropy(p, q) :
zipped = list(zip(p,q))
cross_entropy = 0
for p,q in zipped :
cross_entropy += -p*np.log2(q)
return cross_entropy
세번째 크로스엔트로피 식에서 알 수 있는 사실
- 크로스엔트로피는 p분포와 q분포가 같으면 최소화된다. 두 분포가 같을 때 KL 값이 0 되기 때문이다. 이때 크로스엔트로피 최솟값은 $H[p]$ 가 된다.
- 크로스엔트로피를 최소화 한다는 건 KL 값을 최소화 한다는 것과 같다.
- 크로스엔트로피는 p, q 분포 모양이 다를 수록 커진다.
- 크로스엔트로피는 사실상 p분포와 q분포 모양 다른 정도다.
- 크로스엔트로피 $\ge$ p분포 엔트로피
크로스엔트로피 - 분류모형 성능평가에 사용
p와 q의 모양이 다른 정도(쿨백-라이블러 발산 값과 같다)
정답분포 p와 예측분포 q
설명 :
$KL(p\vert \vert q) = H[p,q] - H[p]$
여기서 분류모형 성능측정할 때는 $H[p]$ 는 0이 된다(정답분포는 원핫인코딩벡터 꼴이기 때문). 따라서
$H[p,q] = KL(p\vert \vert q)$ 이다.
= 데이터 1개에 대한 예측이 틀릴 가능성
= 분류모형의 성능 나쁜 정도
분류모형 성능이 나쁠 수록 크로스엔트로피 증가
분류모형 성능이 좋을 수록 크로스엔트로피 감소
로그손실 - 교차엔트로피 평균
이진분류 문제에서 크로스엔트로피값은 데이터 1개에 대해 예측이 틀릴 가능성(분류모형 성능 나쁜 정도) 을 의미한다.
데이터 N개에 대해 각각의 교차엔트로핏값 평균을 구하면
교차엔트로핏값 평균 : 데이터 N개에 대한 이진분류모형의 성능 나쁜 정도
= 이진분류모형의 손실함수(오차함수)
이 교차엔트로핏값 평균을 로그손실 이라 한다.
로그손실을 최소화 (손실함수 최소화) 시킨다 = 분류모형 성능을 극대화 시킨다.
따라서
로그손실 최소화 = 이진분류모형 성능 최적화 목표.
로그손실 이용해 분류모형 성능 최적화(최대화) 예)
데이터사이언스스쿨 연습문제 10.3.1
사이킷런 패키지 붓꽃 데이터 중에서, 꽃받침 길이 데이터와 꽃받침 폭 데이터 중 어떤 데이터를 사용할 때 분류모형 성능이 극대화 되겠는가?
각 데이터 최솟값과 최댓값 구간을 0.05 간격으로 나눠서 각 값을 기준값 삼아 붓꽃 종을 세토사와 베르시칼라로 분류하자.
1. 꽃받침 길이 데이터 중 특정 기준값으로 붓꽃 종을 분류해보자.
기준값 설정하기 전에, 일단 데이터를 한번 훑어보자.
1
2
3
4
5
6
7
8
9
10
df['sepal length (cm)'].plot()
plt.hlines(5.5, xmin = 0, xmax=100, colors='r')
greater = np.bincount(df[df['sepal length (cm)'] > 5.5]['species'])
less = np.bincount(df[df['sepal length (cm)'] < 5.5]['species'])
g = pd.DataFrame(greater, columns=['5.5 보다 큰'])
l = pd.DataFrame(less, columns=['5.5 보다 작은'])
print(g)
print('-'*10)
print(l)


데이터를 살펴보니 5.5cm 언저리를 기점으로 5.5보다 큰 데이터들은 대체로 정답값이 1로 분류되어 있었고, 5.5보다 작은 값들은 대체로 0번 종으로 분류되어 있었다.
내가 만들 붓꽃 종 분류 모형이 5.5 언저리 특정 기준값을 기준으로 이 값보다 크면 1로 분류하고, 이 값보다 작으면 0으로 분류해야 분류모형이 주어진 정답 값(0,1)을 가장 잘 맞추게 될 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 로그손실 값 그래프 그리는 함수
def plot_log_loss(df, name, reverse=False) :
from sklearn.metrics import log_loss
criteria = np.arange(np.min(df[name]), np.max(df[name])+ 0.05, 0.05)
log_losses = []
for x in criteria :
if reverse == True :
df['y_hat'] = (df[name] < x).astype(int)
log_loss_value = log_loss(df['species'], df['y_hat'])
log_losses.append(log_loss_value)
else :
df['y_hat'] = (df[name] > x).astype(int)
log_loss_value = log_loss(df['species'], df['y_hat'])
log_losses.append(log_loss_value)
plt.plot(criteria, log_losses)
min_log_loss = np.min(log_losses) ; optimized_value = criteria[log_losses.index(min_log_loss)]
plt.scatter(optimized_value, min_log_loss, 30, 'r')
plt.title(f'최저 로그손실 값 : {np.round(min_log_loss, 2)}, 최적해(기준값) : {np.round(optimized_value, 2)}')
plt.xlabel(name)
plt.ylabel('로그손실값')
plt.show()

df[‘종 이름’] > 꽃받침 길이 기준 값
으로 코드를 짜 주어야 특정 기준값보다 큰 값들을 True=1, 작은 값들을 False=0 으로 분류할 것이다.
분류모형의 손실함수인 로그손실값을 각 기준점에서 계산해서 그래프로 그렸더니 위와 같았다.
손실함숫값인 로그손실값이 최소가 될 때가 분류모형 성능이 극대화되는 지점이다.
꽃받침 길이 5.45 cm 를 기준값으로 삼았을 때 로그손실값이 3.8로 최저가 되었다. 곧, 기준값 5.45일 때 분류모형 성능이 가장 극대화된다.
2. 꽃받침 폭 데이터 중 특정값을 기준으로 붓꽃 종을 분류해 보자.
이번에도 실현된 데이터들 특징을 먼저 함 살펴보자.
1
2
3
4
5
6
df['sepal width (cm)'].plot()
plt.hlines(3.0, xmin = 0 , xmax=100, colors='r')
np.bincount(df[df['sepal width (cm)'] > 3]['species']) # 대체로 0
np.bincount(df[df['sepal width (cm)'] < 3]['species']) # 대체로 1
plt.text(20, 4.0, '대체로 0')
plt.text(80, 2.3, '대체로 1')

대체로 3 언저리 특정값을 기준점으로 삼았을 때, 기준값보다 큰 값은 대체로 0번 종이 많았고, 기준값보다 작은 값은 대체로 1번 종이 많았다.
이 경우에는 df[‘종 이름’] < 기준값 으로
코드를 짜야 특정 기준값보다 낮은 값은 True=1 로, 특정 기준값보다 큰 값은 False=0 으로 분류되어 실제 정답값을 잘 맞출 것이다.
이를 위해 ‘로그손실 값 그래프로 그리는 함수’에서, reverse argument 기본값을 False로 주고, 만약 True 가 들어올 경우 원래 df[‘종 이름’] > 기준값 에서 부등호 방향이 < 가 되도록 했다.
1
plot_log_loss(df, 'sepal width (cm)', reverse=True)

꽃받침 폭 특정값을 기준값으로 삼아 각 기준값에서의 로그손실값을 그래프로 그렸다.
기준값이 3.05 일 때 로그손실값이 5.53으로 최저가 되었다.
곧, 꽃받침 폭 3.05cm 를 기준점으로 삼아 데이터들을 종 별로 분류했을 때 분류모형 성능이 가장 극대화 된다는 의미다.
꽃받침 길이 최적값과 꽃받침 폭 최적값 중 로그손실값이 더 작은 값이 분류모형 성능을 더 극대화할 수 있는(종 별 분류를 더 잘 해낼 수 있는) 값이다.
꽃받침 길이 최적값에서 로그손실값이 더 작아졌다. 따라서 꽃받침 길이가 분류모형 성능 극대화에 두 값 중 더 적합한 특징값이다.
쿨백-라이블러발산 (상대엔트로피)
$KL(p\Vert q) = H[p,q] - H[p]$
- 정의 : (임의의 두 분포) q분포가 p분포와 모양 다른 정도
p분포는 비교기준이 된다.
설명)
p분포에서 나온 표본을 q 분포에 따라 추려냈을 때 p분포 표본 1개 당 평균 정보량 - 최적 질문전략 썼을 때 p분포 표본 1개 당 평균 정보량 = KL 발산 값
곧, KL 발산값은 정보량(질문갯수) 차이다.
이 질문갯수 차이는 p분포와 q분포 모양이 비슷할 수록 줄어들고, p분포와 q분포 모양이 다를 수록 커진다.
$\Rightarrow$ KL 발산값 = q분포와 p분포 모양 다른 정도
사이파이 쿨백-라이블러 발산값 계산 코드
기존 사이파이 엔트로피 값 계산 코드에 p와 q 분포를 함께 집어넣으면 된다.
1
sp.stats.entropy(p, q, base=2)
p : 모양 비교기준이 되는 확률분포
q : 기준분포 p와 모양 비교 할 확률분포
쿨백-라이블러발산 성질
- KL 발산 최솟값은 0이다.
p분포와 q분포 모양이 완전히 같을 때 KL 발산값 0 된다.
- $KL \ge 0$
$KL = H[p,q] - H[p]$ 였다. 크로스엔트로피는 언제나 $H[p]$ 보다 같거나 컸다. 따라서 $KL$ 값도 항상 0 또는 양수다.
- $KL(p\Vert q) \ne KL(q\Vert p)$
