함수
정의 :
입력과 출력 사이 일정한 대응’관계’
포인트는 일정한 대응 ‘관계’다.
일정한 대응관계 이기 때문에, 임의의 입력값 하나에는 특정한 출력 1개만 대응될 수 있다.
예)
항상 2에 대해 3이 대응되는 경우 2와 3은 함수관계에 속해있다.
$f(2) = 3$
만약 임의의 입력값에 대해서 출력값이 계속 바뀌면 함수관계 아니다.
예)
$f(2) = 3, f(2) = 5 …$
함수관계 아니다.
정의역
정의 : ‘가능한’ 모든 입력변수들 집합
- 실수 전체를 쓰는 경우가 많다.
공역
정의 : ‘가능한’ 모든 출력변수들 집합
치역
정의 : 출력변수들 집합. 함수관계에서 정의역에 대응됨.
정의역 갯수가 유한할 경우, 함수관계를 표로 나타낼 수 있다.
예)

x와 y가 일정한 대응관계에 있다면, 위 표는 x와 y의 함수관계를 표현한 것이다.
또, 정의역 갯수가 유한한 경우 딕셔너리로 함수관계를 나타낼 수도 있다.
1
2
3
4
# 딕셔너리로 함수 표현하기
f = {3:3.4, 8:1.2, 9:21, 10:23}
f[3] # 3 입력
출력 : 3.4
‘입력과 출력 사이 일정한 대응관계’
한편, 정의역 개수가 무한하면 일일이 표나 딕셔너리로 함수를 나타낼 수 없다.
이때는 파이썬의 함수를 이용하면 이러한 수학 함수를 표현할 수 있다.
예)
1
2
3
# 함수
def f(x) :
return 2*x
함수의 연속과 불연속
불연속
함숫값이 중간에 갑자기 바뀌면 함수가 ‘불연속’ 이다.
함수가 불연속 구간이 있으면 그 구간에서 미분불가능이다.
연속
함수가 불연속이 아니면 연속이다.
연속인 함수는 전 구간 미분가능하다.
데이터분석에 자주 쓰이는 함수 정리
1. 부호함수 (sign function)
정의 : 입력값의 부호를 판별하는 함수
입력값이 양수면 1.
음수면 -1.
0이면 0 출력.
1
2
3
4
5
6
7
8
# 부호함수
def sign(x) :
if x > 0 :
return 1
elif x < 0 :
return -1
else :
return 0
넘파이 부호함수
1
2
# 넘파이 부호함수
np.sign(입력값)
2. 단위계단함수(heavisidestep function)
정의 : 0에서 계단 높이가 1인 함수
입력값이 0 또는 양수 : 1
입력값이 음수 : 0
출력
1
2
3
4
5
6
# 단위계단함수
def heavi_side_step(x) :
if x >= 0 :
return 1
elif x < 0 :
return 0
넘파이 코드는 따로 없다. 만들어 쓰자.
부호함수 & 단위계단함수 그래프
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
xx = np.linspace(-3,3,100)
yy = np.sign(xx)
plt.subplot(211) # plt.subplot(2,1,1)과 같다.
plt.plot(xx, yy, 'ro-')
plt.title('부호함수')
plt.hlines(0, xmin=-3, xmax=3, colors='r', ls=':')
plt.subplot(2,1,2)
plt.title('단위계단함수')
def heavi_side_step(x) :
if x >= 0 :
return 1
elif x < 0 :
return 0
heavi_side_step = [heavi_side_step(x) for x in xx]
plt.plot(xx, heavi_side_step, 'ro-')
plt.suptitle('부호함수와 단위계단함수', y=1.03)
plt.tight_layout()
plt.show()

지시함수
정의 : ‘지시’해둔 값이 입력으로 들어오면 1(True) 출력, 아니면 0(False) 출력하는 함수
$I_{i}(x)$
$I(x=i)$
$i$ 가 미리 지정해놓은 값이다
1
2
3
4
5
6
# 지시함수
def indicator_function(x, i) :
if x == i :
return 1 # true
elif x != i :
return 0 # false
- 지시함수는 표본중에 내가 찾고 싶은 특정 값이 몇 개 있는지 셀 때 유용하다.
예)
$N_{3} = \sum_{i}^{N}{I(x_{i} = 3)}$
1
2
3
4
5
6
7
8
9
10
11
np.random.seed(0)
x = np.random.randint(1,5,100)
def indicator_function(x, i) :
if x == i :
return 1 # true
elif x != i :
return 0 # false
result = np.sum([indicator_function(x, 3) for x in x])
print('3갯수 : {}'.format(result))
3 갯수 : 19
1
np.bincount(x, minlength=10)[3]
19
역함수
정의 : 어떤 함수에서 x와 y 자리를 바꾼 함수.
또는 함수를 $y=x$ 에 대해 대칭시킨 함수를 원래 함수의 ‘역함수’ 라고 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
xx = np.linspace(0,3,300)
def f(x) :
return x**2
def finv(x) :
return np.sqrt(x)
plt.figure(figsize=(4,4))
plt.plot(xx, f(xx), ls='-.')
plt.plot(xx, finv(xx), ls=':')
plt.plot(xx, xx, ls='--', c='g')
plt.axis('equal')
plt.xlim(-1, 3)
plt.ylim(0,3)
plt.title('원래 함수 $y=x^{2}$의 역함수 $(x>0)$')
plt.show()

최대함수
정의 :
입력변수 $x$, $y$ 둘을 입력받아서 둘 중 최댓값을 출력하는 함수
- $x = y$ 인 경우에는 $x$ 를 출력한다.
$max(x,y)$
1
2
3
4
5
6
# 최대함수
def max(x,y) :
if x >= y :
return x
elif x < y :
return y
넘파이 최대함수
1
2
# 넘파이 최대함수
np.maximum(x,y)
최대함수 그래프
1
2
3
4
5
6
7
8
9
10
11
12
# 최대함수 그래프
np.maximum(2,3)
xx = np.linspace(-10,10,1000)
plt.plot(xx, np.maximum(xx,5))
plt.scatter(5,5, 100, 'r')
plt.title('최대함수')
plt.text(8.5, 6.5, '$y=x$')
plt.text(5.4, 5.3, '$y=0$')
plt.text(-2.5, 5.1, '$y=0$')
plt.show()

최소함수
정의 :
입력변수 $x$, $y$ 를 입력받아 둘 중 최솟값을 출력하는 함수.
- $x=y$ 일때는 $x$ 출력한다.
$min(x,y)$
1
2
3
4
5
6
# 최소함수
def min(x,y) :
if x <= y :
return x
elif x > y :
return y
넘파이 최소함수
1
2
# 넘파이 최소함수
np.minimum(x,y)
최소함수 그래프
1
2
3
4
5
6
7
8
9
10
# 최소함수
xx = np.linspace(-3,6,1000)
plt.plot(xx, np.minimum(xx, 3))
plt.scatter(3,3,100, 'r')
plt.text(4,2.8, '$y=3$')
plt.text(3, 2.7, '$y=3$')
plt.text(0, -0.5, '$y=x$')
plt.title('최소함수')
plt.show()

ReLU 함수
정의 :
y값을 0으로 고정시킨 최대함수.
$max(x,0)$
- $x$가 0보다 클 때는 $x$ 출력
- $x$가 0보다 작을 때는 0 출력
- $x=0$ 일때는 $x$출력
1
2
3
4
5
6
# ReLU 함수
def ReLU(x) :
if x >=0 :
return x
elif x < 0 :
return 0
넘파이 ReLU 함수
1
2
# 넘파이 렐루함수
np.maximum(x,0)
ReLU 함수 그래프
1
2
3
4
5
6
7
8
9
10
11
12
# 렐루함수
xx = np.linspace(-5,5,1000)
plt.plot(xx, np.maximum(xx, 0))
plt.xlabel('$x$')
plt.ylabel('$ReLU(x,0)$')
plt.title('$max(x, 0)$ 또는 $ReLU$ 함수')
plt.scatter(0,0, 100, 'r')
plt.text(3, 1.5, '$y=x$')
plt.text(-2, 0.25, '$y=0$')
plt.text(0.1, 0, '$y=0$')
plt.show()

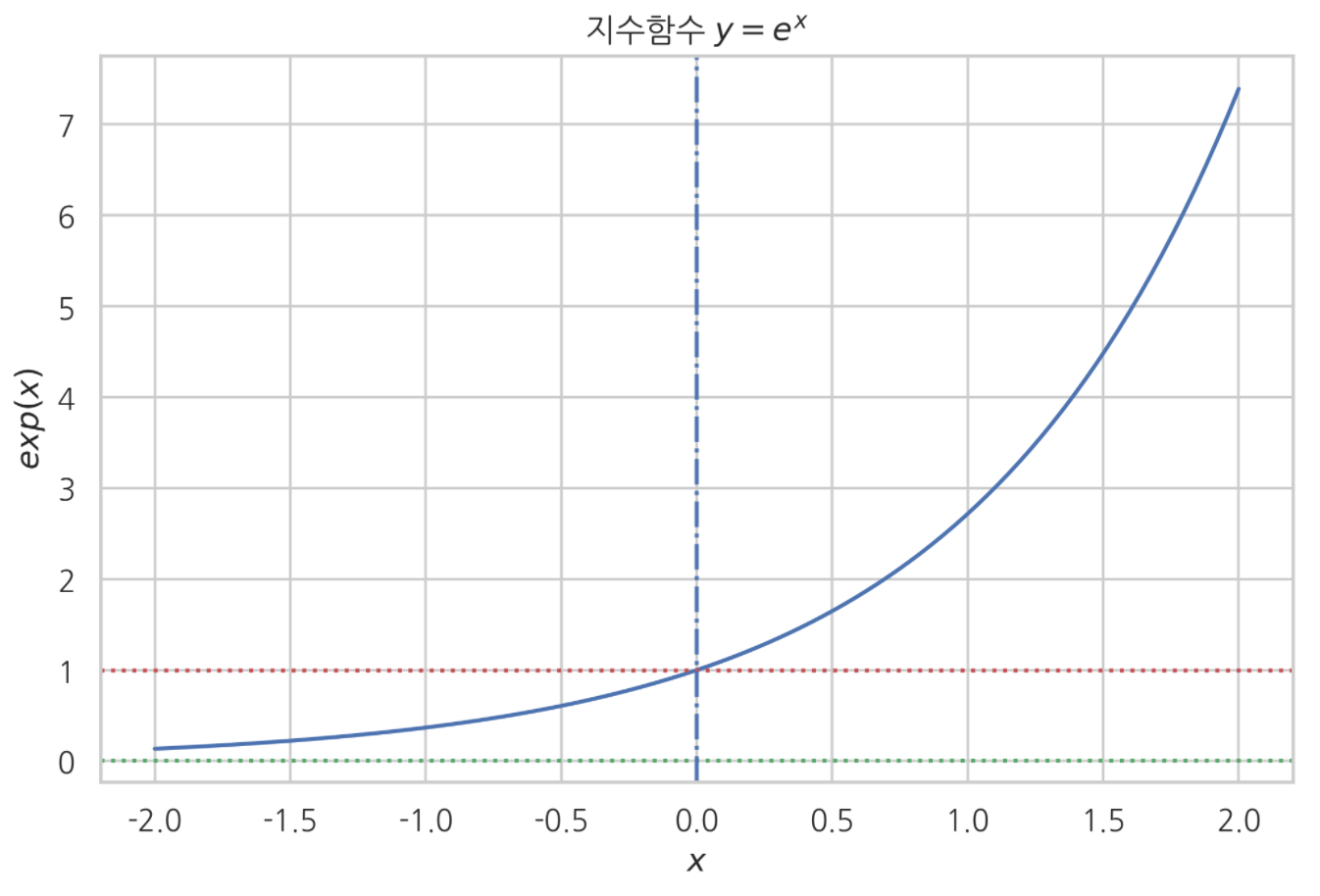
지수함수
정의 :
오일러수 $e$의 거듭제곱으로 이루어진 함수.
$y = e^{x}$
특징 :
- 그래프가 전구간 $x$축 위에 있어서 출력값 항상 양수다.
- $x$ 가 $0$ 일때 출력값이 $1$ 이다.
- $x$가 $+\infty$ 로 갈 때, $y$도 $+\infty$ 로 간다.
- $x_{1}$ > $x_{2}$ 일 때, $f(x_{1})$ > $f(x_{2})$ 이다.
지수함수 그래프
1
2
3
4
5
6
7
8
9
10
11
xx = np.linspace(-2,2,100)
yy = np.exp(xx)
plt.plot(xx,yy)
plt.title('지수함수 $y=e^{x}$')
plt.xlabel('$x$')
plt.ylabel('$exp(x)$')
plt.axhline(1, ls=':', c='r')
plt.axhline(0, ls=':', c='g')
plt.axvline(0, ls='-.', c='b')
plt.show()
로지스틱함수 (시그모이드함수)
정의 :
지수함수의 변형함수.
회귀분석, 인공신경망 등에 자주 쓰인다.
$y = \frac{1}{1+e^{(-x)}}$
1
2
3
4
5
6
7
8
9
10
11
12
13
# 로지스틱함수
xx = np.linspace(-10,10,100)
def plot_logistic(x) :
return 1/(1+np.exp(-x))
yy = plot_logistic(xx)
plt.plot(xx, yy)
plt.title('로지스틱함수(시그모이드함수)')
plt.xlabel('$x$')
plt.ylabel('$logistic(x)$')
plt.show()

로그함수
정의 :
지수함수 $y=e^{x}$ 의 역함수.
$y = \log_{e}{x}$
$y = \log{x}$
특징 :
- $x$ > $0$ 인 구간에서만 정의된다.
- $x = 1$ 일 때 출력값 $0$ 이다.
- $x$가 $0$을 향해 다가갈 때, $y$는 $-\infty$ 를 향해 다가간다.
- $x_{1}$ > $x_{2}$ 일 때, $f(x_{1})$ > $f(x_{2})$ 가 성립한다.
로그함수 그래프
1
2
3
4
5
6
7
8
9
10
11
12
13
# 로그함수
xx = np.linspace(-10,10,1000)
yy = np.log(xx)
plt.title('$\log_{e}{x}$ 로그함수')
plt.plot(xx, yy, 'r')
plt.axvline(0, c='b', ls=':')
plt.axvline(1, c='b', ls=':')
plt.axhline(0, c='g', ls='-.')
plt.scatter(1,0, 100, 'r')
plt.xlabel('$x$')
plt.ylabel('$\log_{e}{(x)}$')
plt.show()

로그함수의 몇 가지 유용한 성질
1. 로그는 곱셈을 덧셈으로 바꿔준다.
$\log{(ab)} = \log{a}+\log{b}$
많은경우, 로그 씌우면 계산이 편해진다.
예) 로그가능도함수
2. 정의역이 양수만으로 구성되어 있을 때, 최적화 목적함수에 로그 씌워도. 최소점,최대점 위치는 바뀌지 않는다.
최적화 할 때 매우 유용하다.
최적화의 목적은 최소출력, 최대출력을 만드는 최적해 찾기다.
목적함수에 로그 씌워도 함수 높낮이는 변할지언정 최소점, 최대점은 변하지 않는다.
곧, 최적해는 그대로라는 말이다.
따라서 목적함수에 로그 씌울 때 계산이 더 편한 경우 로그 씌우고 최적화 할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def ff(x) :
return x**3-12*x+20*np.sin(x) + 7
xx = np.linspace(-4,4,300)
yy = ff(xx)
plt.subplot(2,1,1)
plt.plot(xx, yy)
plt.title('$x^{3}-12x+20\sin(x) + 7$')
plt.xlabel('$x$')
plt.ylabel('f(x)')
plt.axhline(np.max(yy), ls=':', c='k')
plt.axhline(np.min(yy), ls=':', c='k')
plt.axvline(xx[np.argmax(yy)], c='g')
plt.axvline(xx[np.argmin(yy)], c='g')
plt.subplot(2,1,2)
plt.plot(xx, np.log(yy))
plt.axhline(np.max(np.log(yy)), ls=':', c='r')
plt.axhline(np.min(np.log(yy)), ls=':', c='r')
plt.axvline(xx[np.argmax(np.log(yy))], c='g')
plt.axvline(xx[np.argmin(np.log(yy))], c='g')
plt.title('$\log(x^{3}-12x+20\sin(x) + 7)$')
plt.ylabel('$\log{f(x)}$')
plt.suptitle('최적화 목적함수 $f(x)$에 로그 취해도 최적해 위치는 같다', y=1.03)
plt.tight_layout()
plt.show()

3. 0~1 사이 고만고만한 값들 로그 씌우면. 값들 간 간격을 $-\infty$ 부터 $0$ 사이로 쭉쭉 늘려준다.
따라서 비슷비슷한 값들 간 비교가 쉬워진다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
np.random.seed(0)
x = np.random.rand(5)
x = x/np.sum(x)
plt.subplot(211)
plt.bar(np.arange(1,6), x)
plt.ylim(0, 1)
plt.ylabel('$x$')
plt.title('0, 1 사이 숫자들의 $\log$ 변환')
plt.subplot(212)
sns.barplot(np.arange(1,6), np.log(x))
plt.ylabel('$\log{x}$')
plt.show()

소프트플러스 함수
지수함수와 로그함수를 합쳐놓은 형태다.
$y = \log{(1+e^{x})}$
- $x=0$ 부근에서 함수가 부드럽게 증가한다.
- 렐루함수와 비슷하게 생겼다.
- 하지만 렐루함수는 $x=0$ 에서 불연속이기 때문에 $x=0$ 지점에서 미분불가능하다. 반면 소프트플러스함수는 $x=0$ 지점에서 연속이기 때문에 미분가능하다.
1
2
3
# 소프트플러스 함수
def plot_softplus(xx) :
return np.log(1+np.exp(xx))
1
2
3
4
5
6
7
8
9
10
# 소프트플러스 함수 그래프
xx = np.linspace(-10,10,1000)
yy = plot_softplus(xx)
plt.plot(xx, yy)
plt.suptitle('소프트플러스 함수', y=1.03)
plt.title('장점 : 전 구간 미분가능(연속)')
plt.xlabel('$x$')
plt.ylabel('$\zeta(x)$')
plt.show()

다변수함수
정의 :
다차원 벡터 입력 받아 스칼라 출력하는 함수
$f(x_{1}, x_{2})$
입력벡터 $x$
$x = [x_{1}, x_{2}]$
$n$차원 함수 :
다변수함수를 입력벡터 차원에 따라 $n$차원 함수라고도 부른다.
예) 입력벡터 : 2차원 벡터
$\Rightarrow$ 2차원 함수
2차원 함수를 그래프로 표현하기
예를 들어 입력벡터 차원이 2차원인 다변수함수는 2차원 함수다.
2차원 함수는 그래프로 표현하면 3차원 형상으로 표현된다.
(마치 3차원 지형과도 같다)
2차원 함수를 3차원 그래프로 표현해보자.
$f(x,y) = 2x^{2}+6xy+7y^{2}-26x-54y+107$
위 2차원 다변수함수로 3차원 서피스 플롯, 컨투어플롯을 그려보자.
3차원 서피스플롯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 3차원 서피스플롯
def f(x,y) :
return 2*x**2+6*x*y+7*y**2-26*x-54*y+107
xx = np.linspace(-10,10,100)
yy = np.linspace(-10,10,100)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(X,Y,Z,linewidth=0.3, cmap='BrBG')
ax.view_init(40, -110)
plt.xlabel('$x$')
#plt.ylabel('$y$')
ax.set_zlabel('$z$')
plt.title('3차원 서피스 플롯')
ax.set_zticks([])
ax.set_xticks([])
ax.set_yticks([])
plt.show()

컨투어플롯
1
2
3
4
5
6
CS = plt.contour(X,Y,Z, levels=np.logspace(0,3,10))
plt.clabel(CS, fmt= '%d')
plt.title('컨투어 플롯')
plt.ylim(-10,10)
plt.xlim(-10,10)
plt.show()

위 컨투어 플롯을 다시 서피스플롯으로 표현해보자.
1
2
3
4
5
6
7
ax = plt.gca(projection='3d')
ax.plot_surface(X,Y,Z, linewidth=0.3, cmap='RdYlGn')
ax.view_init(30,100)
ax.set_zticks([])
ax.set_yticks([])
ax.set_xticks([])
plt.show()
위 서피스플롯(가운데가 들어가고 바깥쪽이 위로 솟는) 을 위에서 바라본 것이 앞에서 그렸던 컨투어플롯이다.
분리가능 다변수함수
정의 :
$f(x,y) = f_{1}(x)f_{2}(y)$.
2차원 다변수함수 $f(x,y)$ 가 있을 때, 이를 $f_{1}(x)f_{2}(y)$ 로 나타낼 수 있으면. ‘분리가능 다변수함수’ 라고 한다.
두 확률변수가 독립일 때, 두 확률변수에서 나온 모든 표본들은 서로 독립이었다.
확률에서 두 사건이 독립인 경우, 다음과 같은 성질이 있었다.
$p(x,y) = p(x)p(y)$
결합확률밀도함수를 주변확률밀도함수 곱 으로 표현가능했다.
이때의 결합확률밀도함수 또한 분리가능 다변수함수라고 볼 수 있다.
$f(x,y) = f(x)f(y)$
$p(x,y) = p(x)p(y)$
분리가능 다변수함수 단면모양은 모두 같다
위 경우 분리가능 다변수함수는 2차원 함수다.
2차원 함수는 3차원 그래프로 나타낼 수 있다.
예를 들면 이렇게 생겼다는 거다.
(아래 이미지는 2차원 함수를 3차원 그래프로 나타낸 예시일 뿐, 분리가능다변수함수와는 상관 없다.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 2차원 함수의 3차원 그래프 예시
mu = np.array([1,0])
rv = sp.stats.multivariate_normal(mu)
xx = np.linspace(-5,5,100)
yy = np.linspace(-5,5,100)
X,Y = np.meshgrid(xx,yy)
ax = plt.gca(projection='3d')
ax.plot_surface(X,Y, rv.pdf(np.dstack([X,Y])), linewidth=0.2, cmap='coolwarm')
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
plt.title('2차원 함수의 입체 3차원 그래프 예시')
plt.show()

이렇게 3차원 ‘지형’과도 같은 2차원 함수는 $x$ 또는 $y$ 값을 고정한 채 케이크 썰듯이 단면을 자를 수 있다.
예를 들면 $y$ 값을 $3$ 으로 고정한 채 $x$ 값만 전 구간 변화시키면 $x$변수에 대한 그래프는 위 3차원 도형을 $y=3$ 에서 칼로 자른 단면이 된다.
분리가능다변수함수의 경우, 이 단면 모양이 모두 같다.
$p(x,y) = p(x)p(y)$
if $ y = y_{0}, $
$p(x, y_{0}) = p(x)p(y_{0})$
위 식에서 $p(x, y_{0})$ 은 $x$ 변수만 갖는 단변수함수가 된다.
또, 3차원 도형을 $y=y_{0}$ 지점에 고정시켜놓고 자른 단면을 표현한 것이다.
$p(x)p(y_{0})$ 에서, $p(y_{0})$ 은 $y_{0}$ 값에 따라 변하는 특정 상수다.
그러면,
$k_{0}p(x)$ 이다.
결국
$p(x, y_{0}) = k_{0}p(x)$ 가 된다.
마지막 수식 의미는.
$p(x,y)$ 를 $y=y_{0}$ 에서 자른 단면은 $k_{0}p(x)$ 와 같다는 것이다.
$k_{0}p(x)$ 는 모양은 $p(x)$ 이고, 그 높이가 $k_{0}$ 에 따라 변한다.
반대로 $x = x_{0}$ 으로 고정시켰을 때도 똑같이 성립한다.
결국 분리가능다변수함수 $p(x,y) = p(x)p(y)$ 단면은 모양은 $p(x)$ 또는 $p(y)$ 로 모두 같고, 그 높이만 다르다.
$\Rightarrow$ 분리가능다변수함수 단면은 모양이 모두 같다!
시각적으로 나타내면 아래와 같다.

가운데 가장 큰 컨투어플롯이 분리가능다변수함수의 그래프다.
위쪽 $g_{1}(x)$ 는 $y=y_{0}$에 고정시켜 놓고 분리가능다변수함수를 케잌 자르듯 자른 단면들이다.
보면 높이는 다르지만 모양은 다 같은 걸 볼 수 있다.
다변수 다출력 함수
정의 :
단변수함수는 스칼라를 입력받아 스칼라를 출력하는 스칼라함수이다.
다변수함수는 다차원벡터를 입력받아 스칼라를 출력하는 스칼라함수이다.
다변수다출력함수는 다차원벡터를 입력받아 다차원벡터를 출력하는 벡터함수이다.
소프트맥스 함수
다변수 다출력함수의 대표적 예다.
다차원 벡터 입력받아 다차원 벡터 출력한다.
주요 기능 및 특징 :
다차원벡터를 입력 받아 벡터 각 원소 꼴을 ‘확률 꼴’로 바꿔서 출력해주는 함수다.
물론 출력은 벡터다.
- 출력벡터 각 원소는 0과 1 사이 값이다.
- 출력벡터 각 원소 총합 $=1$ 이다.
- 입력벡터 원소 크기 순서가 출력벡터에서 그대로 유지된다.
쓰임 :
주로 인공신경망 끝단에 사용되어서 인공신경망의 출력을 입력받아 확률 꼴로 바꿔 다시 출력한다.
수식 :
$softmax(x_{1}, x_{2}, x_{3}) =$
$[\frac{exp(w_{1}x_{1})}{exp(w_{1}x_{1})+exp(w_{2}x_{2})+exp(w_3, x_{3})}, \frac{exp(w_{2}x_{2})}{exp(w_{1}x_{2})+exp(w_{2}x_{2})+exp(w_{3}x_{3})}, \frac{exp(w_{3}x_{3})}{exp(w_{1}x_{2})+exp(w_{2}x_{2})+exp(w_{3}x_{3})}]^{T}$
파이썬 코드로 표현한 소프트맥스함수 :
1
2
3
4
# 소프트맥스 함수
def softmax(x,w) :
e = np.exp(w*x)
return e/np.sum(e)
예)
소프트맥스 함수를 사용해서 임의의 입력벡터 각 원소를 ‘확률 꼴’ 로 바꿔 출력해보자.
$x = [2, 0.8, 1]$ 을 입력벡터로 쓰겠다.
가중치벡터 $w$는 1벡터 $1_{3} = [1,1,1]$ 쓰겠다.
1
2
3
4
5
6
7
8
9
10
# 소프트맥스함수 사용 예
w = np.ones(3)
x = np.array([2,0.8,1])
def softmax(x,w) :
e = np.exp(w*x)
return e/np.sum(e)
y = softmax(x,w)
y, np.sum(y)

벡터 $x = [2,0.8, 1]$ 을 소프트맥스 함수에 넣은 결과물을 보면
- 출력벡터 각 원소는 0과 1 사이 값이다.
- 출력벡터 모든 원소 합은 1이다.
- 입력벡터 크기 순서가 출력벡터에서 그대로 유지된다.
소프트맥스 함수 출력의 세 가지 주요 특징이 그대로 성립한다.
입력벡터 $x$ 를 받아 이 벡터 각 원소를 ‘확률 꼴’로 바꿔 출력했음을 확인할 수 있다.
가중치가 커지면 최댓값_최솟값 사이 간격 더 벌어진다 :
소프트맥스 함수에서는 가중치벡터 $w$ 각 원소 값(가중치)들이 커지면, 입력벡터의 최댓값과 최솟값 사이 간격이 각 출력값에서 더 벌어진다.
1
2
# 예) 가중치 크기 1-> 3 으로 증가
softmax(x, 3*w)
예를 들어 모두 $1$ 이었던 가중치 $w_{1}, w_{2}, w_{3}$ 크기를 $3$ 으로 증가시켜보았다.

가중치를 증가시켰을 때, 출력벡터는 위와 같다.
앞에서 가중치 1일 때 출력은 아래와 같았다.

가중치 1이었을 때는 최댓값과 최솟값이 0.59 _ 0.18 로 바뀌어 출력됬다면, 가중치 3일 때는 최댓값 최솟값이 0.92 _ 0.02 로 둘 사이 간격이 훨씬 멀어졌음을 볼 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
plt.subplot(2,1,1)
plt.xlim(0, 1)
plt.axhline(0, c='b', ls=':')
plt.scatter(0.18045591, 0, 100, 'r')
plt.scatter(0.59913473, 0, 100, 'r')
plt.text(0.2, 0.02, '최솟값')
plt.text(0.55, 0.02, '최댓값')
plt.hlines(0, xmin=0.18, xmax=0.6, colors='g')
plt.title('가중치 1일 때')
plt.subplot(2,1,2)
plt.xlim(0,1)
plt.axhline(0, c='b', ls=':')
plt.scatter(0.02536761, 0, 100, 'b')
plt.scatter(0.9284096, 0, 100, 'b')
plt.text(0.03, 0.015, '최솟값')
plt.text(0.92, 0.015, '최댓값')
plt.hlines(0, xmin=0.03, xmax=0.92, colors='g')
plt.title('가중치 3일 때')
plt.suptitle('소프트맥스 함수 출력의 최댓값_최솟값 사이 거리 변화')
plt.tight_layout()
plt.show()

함수 평행이동
정의 :
‘출력’을 이동하라 (입력이 그대로 일 때)
설명)
함수는 ‘입력과 출력 사이 일정한 대응관계’였다.
만약 $A$ 라는 입력에 출력이 1만 대응된다면, $A$ 와 1은 함수관계가 있다.
하지만 같은 입력에 출력이 무작위로 바뀐다면, 둘은 함수관계가 있다고 말할 수 없다.
곧, 함수관계에서는 어떤 입력에 특정한 출력이 대응된다고 정리할 수 있다.
함수가 ‘대응관계’라면, 함수 평행이동은 ‘대응관계’를 이동시켜라는 의미다.
이는 대응관계를 어떤 특정 방식으로 ‘변화’시켜라는 의미로 해석할 수도 있다.
대응관계를 변화시킨다는 말은, 기존 입력값들에 대해 이제부터 다른 출력값들이 대응되게 한다는 말과 같다.
따라서, 함수를 평행이동시킨다는 건 입력은 유지시키면서 출력을 변화시킨다는 뜻과 같다.
함수평행이동 = [출력 이동]
그러면 입력값들이 같을 때, 기존 입력값에 어떤 출력이 새로 대응되어야 함수가 ‘평행이동’ 할까?
예를 들어 함수를 오른쪽으로 2.5만큼 평행이동 하고싶다면 뭘 새로 대응시켜야 할까?
함수 $f(x)$ 의 입력값 $x$ 가 있다고 하자.
$x$에 대응되는 출력값은 $f(x)$ 다.
함수 $f(x)$ 를 오른쪽으로 $2.5$ 만큼 이동시키려면, 원래 $x$보다 2.5만큼 뒤에 있던 점의 함숫값이 $x$에 대응되어야 한다.
곧, $x$에 대해 $f(x-2.5)$ 가 대응되어야 한단 뜻이다.
평행이동 전 함수 $f(x)$의 정의역 모든 원소들에 똑같이 $f(x-2.5)$ 를 대응시키면, 결과적으로 함수가 오른쪽으로 $2.5$ 만큼 이동한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 함수 평행이동
xx = np.linspace(-10,10,100)
plt.plot(xx, plot_logistic(xx), c='c', label='f(x)')
plt.scatter(2.5,0, 100, 'c')
plt.text(2.3, 0.05, '$x$')
plt.scatter(0,0,100, 'm')
plt.text(-0.05,0.05, '$x-2.5$')
plt.scatter(0, plot_logistic(0), 100, 'm')
plt.hlines(0, xmin=0.3, xmax=2.2, colors='m')
plt.annotate('', xy=[2.5, plot_logistic(0)], xytext=[0, plot_logistic(0)], arrowprops={'facecolor' : 'm'})
plt.scatter(2.5, plot_logistic(0), 100, 'm')
plt.text(2.65, 0.55, '$f(x-2.5)$')
plt.text(-2.3, 0.55, '$f(x-2.5)$')
plt.vlines(2.5, ymin=0.03, ymax=plot_logistic(0), colors='r', ls=':')
plt.scatter(2.5, plot_logistic(2.5), 100, 'm')
plt.annotate('', xy=[5, plot_logistic(2.5)], xytext=[2.5, plot_logistic(2.5)], arrowprops={'facecolor' : 'm'})
plt.scatter(5, plot_logistic(2.5), 100, 'm')
plt.scatter(1.02, plot_logistic(1.02), 100, 'm')
plt.annotate('', xy=[3.52, plot_logistic(1.02)], xytext=[1.02, plot_logistic(1.02)], arrowprops={'facecolor' : 'm'})
plt.scatter(3.52, plot_logistic(1.02), 100, 'm')
plt.plot(xx, plot_logistic(xx-2.5), c='m', ls=':', label='f(x-2.5)')
plt.title('함수 평행이동 원리')
plt.xlabel('$x$')
plt.legend()
plt.show()

결국 함수를 오른쪽으로 2.5만큼 이동하고 싶으면
$f(x) \Rightarrow f(x-2.5)$
하면 되는 것이다.
정리 및 요약 :
- 함수를 오른쪽으로 2.5만큼 이동 :
$f(x) \Rightarrow f(x-2.5)$
- 함수를 왼쪽으로 2.5만큼 이동 :
$f(x) \Rightarrow f(x+2.5)$
- 함수를 위로 2.5만큼 이동 :
$f(x) \Rightarrow f(x)+2.5$
- 함수를 아래로 2.5만큼 이동 :
$f(x) \Rightarrow f(x)-2.5$
함수 평행이동 예)
로지스틱함수를 오른쪽으로 5 이동, 아래로 1 이동 해보자.
$f(x) \Rightarrow f(x-5)-1$
1
2
3
4
5
6
7
8
# 로지스틱함수 오른쪽으로 5, 아래로 1 이동
xx = np.linspace(-10,10,1000)
plt.plot(xx, plot_logistic(xx), c='m', label='$\sigma(x)$')
plt.plot(xx, plot_logistic(xx-5)-1, c='c', label='$\sigma(x-5)-1$')
plt.title('로지스틱함수 오른쪽으로 5 이동, 아래로 1 이동')
plt.xlabel('$x$')
plt.legend()
plt.show()

다변수함수 평행이동
다변수함수 평행이동도 본질은 같다.
다만 y축 방향으로 평행이동 할 때 좀만 더 주의 기울이면 된다.
만약 다변수함수를 y축방향으로 $+0.75$ 하고싶다면 어떻게 해야 할까?
y축 방향으로 $+0.75$ 이동한다는 건 y축 관점에서는 함수를 오른쪽으로 0.75만큼 이동한다는 거다. 따라서 기존 y 값에 $f(y-0.75)$ 값을 대응시키면 x축 관점에서는 함수가 y축 방향으로 $+0.75$ 만큼 이동한다.
정리하면 다음곽 같다.
다변수함수 평행이동 정리
- x축 방향으로 +a, y축 방향으로 +b 만큼 이동 :
$f(x) \Rightarrow f(x-a, y-b)$
- x축 방향으로 +a, y축 방향으로 -b 만큼 이동 :
$f(x) \Rightarrow f(x-a, y+b)$
- x축 방향으로 -a, y축 방향으로 +b 만큼 이동 :
$f(x) \Rightarrow f(x+a, y-b)$
- x축 방향으로 -a, y축 방향으로 -b 만큼 이동 :
$f(x) \Rightarrow f(x+a, y+b)$
다변수함수 평행이동 예)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 다변수함수 오른쪽으로 0.7, 위로 0.8 이동
xx = np.linspace(-1,1,100)
yy = np.linspace(-1,1,100)
def g(x,y) :
return np.exp(-x**2-16*y**2)
X,Y = np.meshgrid(xx,yy)
Z = g(X,Y)
Z2 = g(X-0.7, Y-0.8)
plt.contour(X,Y,Z)
plt.contour(X,Y,Z2, linestyles=':')
plt.ylim(-0.5, 1)
plt.text(-0.02, 0.02, '$f(x,y)$')
plt.text(0.6, 0.8, '$f(x-0.7, y-0.8)$')
plt.title('다변수함수의 평행이동')
plt.annotate('', xy=[0.75, 0.0], xytext=[0,0], arrowprops={'facecolor' : 'red'})
plt.annotate('', xy=[0.75, 0.8], xytext=[0.75, 0.0], arrowprops={'facecolor' : 'blue'})
plt.show()

함수 스케일링
정의 :
“축 방향으로 함수 잡아 늘리기”
- 함수를 x축 방향으로 $a$ 배 늘리고 싶다면 :
$f(x) \Rightarrow f(\frac{x}{a})$
- 함수를 y축 방향으로 $b$ 배 늘리고 싶다면 :
$f(x) \Rightarrow bf(x)$
함수 스케일링 예)
1
2
3
4
5
6
7
8
9
# 로지스틱 함수를 x축 방향으로 1/5배, y축 방향으로 5배 스케일링
xx = np.linspace(-10,10,1000)
plt.plot(xx, plot_logistic(xx), label='$f(x)$')
# x축으로 1/5배, y축 방향으로 5배 늘리자.
plt.plot(xx, 5*plot_logistic(5*xx), label='5$f(5x)$', ls=':')
plt.legend()
plt.title('로지스틱함수 스케일링 : x축으로 1/5배, y축으로 5배 스케일링 결과')
plt.show()

