전역 최적화 문제
정의 :
최적화를 통해 함수 전역 최저점을 찾는 문제
내가 어떤 최적화 결과를 얻었는데, 그 최적점이 함수 전역의 최적점이라고 확신할 수 있는가?
만약 함수형태가 컨벡스함수(볼록함수) 라면, 함수 전역 최저점이라고 생각할 수 있을 것이다.
반면에 함수가 전역 최저점 말고도 여러 개의 국소 최저점을 갖고 있다면?
내가 얻은 최적화 결과가 전역 최저점이라고 단정지어 말하기 어렵다.
곧, 함수에 여러 개의 국소 최저점이 존재하는 경우. 스텝사이즈 나 최적화 시작 위치 등에 따라
최적화 결과가 전역 최저점이 아닌 국소 최저점 일 수 있다.
최적화 결과가 전역이 아닌 국소 최저점에 수렴한 예)
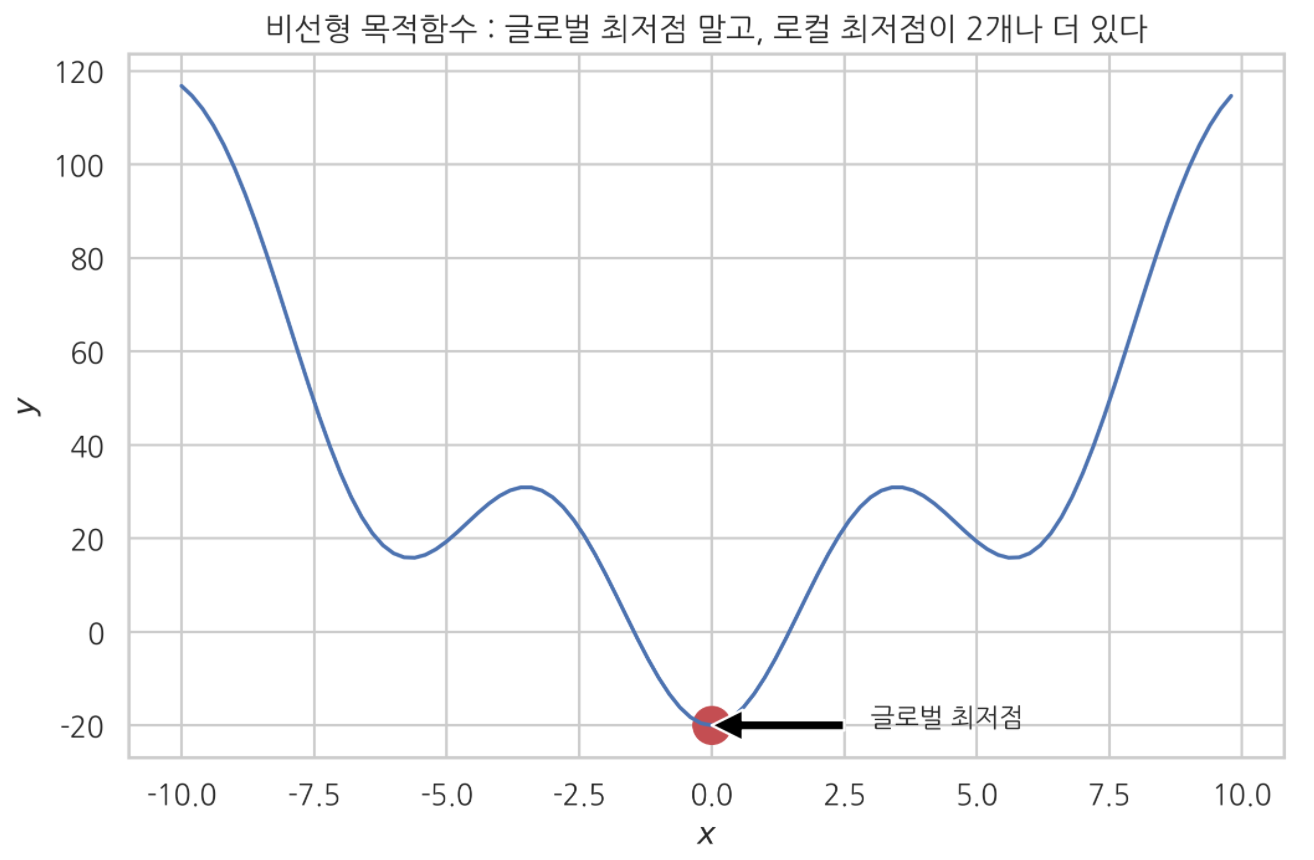
나는 이 목적함수를 대상으로 전역 최적화 문제를 풀고 싶다.
함수 가장 아래쪽 ‘글로벌 최저점’에 수렴하는 게 목표다.
비선형 목적함수 최적화 : 최대경사법 알고리듬 사용
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 위 비선형 목적함수 직접 최적화 해보자.
# 최대경사법
import sympy
x = sympy.symbols('x')
f = x**2-20*sympy.cos(x)
sympy.diff(f, x)
def gradient(x) :
return 2*x+20*np.sin(x)
def f_non_linear(x) :
return x**2-20*np.cos(x)
x = np.arange(-10,10,0.2)
plt.plot(x, f_non_linear(x))
mu = 0.03
# 최적화 시작점
a = -7.5
for i in range(50) :
plt.plot(a,f_non_linear(a), 'go', markersize=5)
next_ = a - mu*gradient(a)
a = next_
plt.plot(a, f_non_linear(a), 'ro', markersize=5)
plt.text(a-2, f_non_linear(a)-12, '로컬 최저점에 수렴')
plt.suptitle('비선형 목적함수 최대경사법 최적화', y=1.003)
plt.title(f'시작점 : [-7.5, {np.round(f_non_linear(7.5),2)}], 결과 : 왼쪽 로컬 최저점 수렴')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

$[-7.5, 49.32]$ 에서 시작한 결과 전역 최저점이 아닌 왼쪽 로컬 최저점에 수렴했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
x = np.arange(-10,10,0.2)
plt.plot(x, f_non_linear(x))
mu = 0.03
# 최적화 시작점
a = 7.5
for i in range(50) :
plt.plot(a,f_non_linear(a), 'go', markersize=5)
next_ = a - mu*gradient(a)
a = next_
plt.plot(a, f_non_linear(a), 'ro', markersize=5)
plt.text(a-2, f_non_linear(a)-12, '로컬 최저점에 수렴')
plt.suptitle('비선형 목적함수 최대경사법 최적화', y=1.003)
plt.title(f'시작점 : [7.5, {np.round(f_non_linear(7.5),2)}], 결과 : 오른쪽 로컬 최저점 수렴')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

같은 최대경사법 알고리듬으로, 시작점 $[7.5, 49.32]$ 에서 최적화를 시작해봤다.
결과는 오른쪽 로컬 최저점에 수렴했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
x = np.arange(-10,10,0.2)
plt.plot(x, f_non_linear(x))
mu = 0.03
# 최적화 시작점
a = 2.5
for i in range(50) :
plt.plot(a,f_non_linear(a), 'go', markersize=5)
next_ = a - mu*gradient(a)
a = next_
plt.plot(a, f_non_linear(a), 'ro', markersize=5)
plt.text(a-2, f_non_linear(a)-12, '글로벌 최저점에 수렴')
plt.suptitle('비선형 목적함수 최대경사법 최적화', y=1.003)
plt.title(f'시작점 : [{2.5}, {np.round(f_non_linear(2.5),2)}], 결과 : 글로벌 최저점 수렴')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

한편 시작점을 $[2.5, 22.27]$ 로 잡았을 때는 최적화 결과가 전역 최저점에 수렴했다.
이처럼, 함수에 여러 개의 국소 최저점이 있는 경우.
시작점이 어디냐에 따라 최적화 결과가 전역 최저점에 수렴하지 않을 수 있었다.
비선형 목적함수 최적화 : 뉴턴방법 알고리듬 사용
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 뉴턴방법
plt.subplot(1,3,1)
x = np.arange(-10,10,0.2)
plt.plot(x, f_non_linear(x))
a = 1.5
plt.title(f'시작점 : {a}')
for i in range(100) :
plt.plot(a, f_non_linear(a), 'go', markersize=5)
next_ = a - g(a)/h(a)
a = next_
plt.subplot(1,3,2)
x = np.arange(-10,10,0.2)
plt.plot(x, f_non_linear(x))
a = 1.2
plt.title(f'시작점 : {a}')
for i in range(100) :
plt.plot(a, f_non_linear(a), 'go', markersize=5)
next_ = a - g(a)/h(a)
a = next_
plt.subplot(1,3,3)
x = np.arange(-10,10,0.2)
plt.plot(x, f_non_linear(x))
a = 4
plt.title(f'시작점 : {a}')
for i in range(100) :
plt.plot(a, f_non_linear(a), 'go', markersize=5)
next_ = a - g(a)/h(a)
a = next_
plt.suptitle('뉴턴 : 비선형함수 모양이 2차함수 모양과 다르고, 로컬최저점이 많아서 제대로 최적화 안 된다', y = 1.03)

비선형 목적함수 최적화 : 준 뉴턴방법(BFGS)
1
sp.optimize.minimize(f_non_linear, 4)
컨벡스 최적화
정의 :
컨벡스 함수를 대상으로 최적화(최소화) 하는 방법
- 컨벡스 최적화 결과는 항상 전역 최적해다.
컨벡스 필요조건 :
- DCP rule
컨벡스 필요조건을 DCP rule 이라고 한다.
목적함수가 DCP rule 을 만족하면, 그 함수는 무조건 컨벡스 함수다.
하지만 컨벡스 함수인데 DCP rule 만족하지 않는 경우도 왕왕 있다.
DCP rule $\rightarrow$ $Convex$
$Convex$ $\nrightarrow$ DCP rule
함수가 DCP rule 을 만족하지 않지만, 컨벡스 함수인 예
목적함수 : $2x_{1}^{2} +x_{2}^{2}+x_{1}x_{2}+x_{1}+x_{2}$
제한조건 :
$x_{1} + x_{2} = 1$
$x_{1} \ge 0$
$x_{2} \ge 0$
위 목적함수, 그리고 제한조건을 고려한 목적함수의 최소화 문제도 DCP rule 을 만족하지 않는다.
1
2
3
4
5
6
7
8
# 목적함수가 DCP rule 만족하지 않는다
import cvxpy as cp
x1 = cp.Variable()
x2 = cp.Variable()
obj = 2*x1**2+x2**2+x1*x2+x1+x2
obj.is_dcp()

1
2
3
4
5
6
7
# 최소화 문제도 DCP rule 만족하지 않는다
obj = cp.Minimize(obj)
cons = [x1+x2 == 1]
prob = cp.Problem(obj, constraints=cons)
prob.is_dcp()

하지만, 이 함수를 그려보면
1
2
3
4
5
6
7
def f(x,y) :
return 2*x**2+y**2+x*y+x+y
Z = f(X,Y)
ax = plt.gca(projection='3d')
ax.plot_surface(X,Y,Z, linewidth=0.03, cmap='flare')
ax.view_init(10, -60)
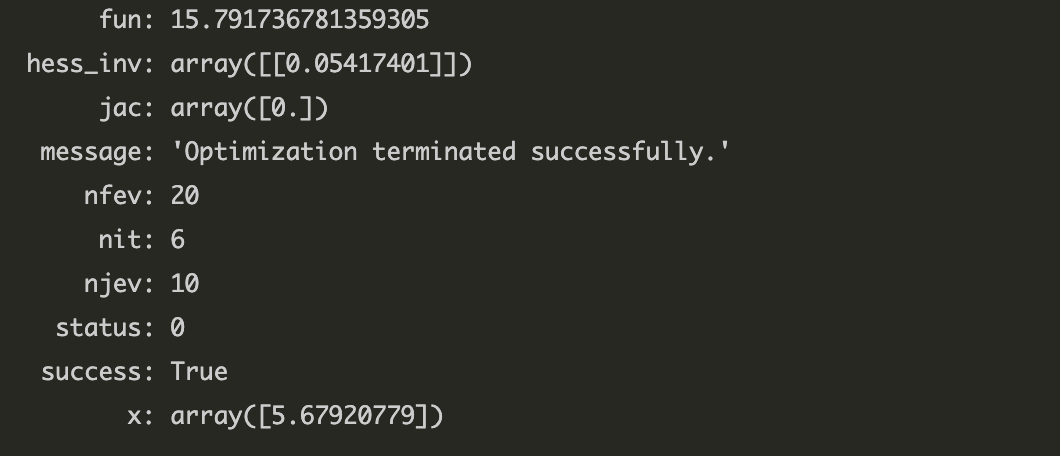
plt.title('컨벡스 함수지만 DCP rule 만족하지 않는 것들도 있다')

모양이 아래에서 봤을 때 볼록한, 컨벡스 함수임을 확인할 수 있다.
따라서 어떤 함수가 DCP rule 에 어긋나지만. 컨벡스 함수인 경우도 존재한다.
(위 예시의 함수는 이차계획법 문제로 고쳐서 CVXOPT 의 solver.qp 명령으로 컨벡스 최적화 할 수 있다)
(DCP rule에 대해서는 아래 CVXPY 부분에 좀 더 자세하게 기록해두었다)
컨케이브(오목) 함수 최대화도 컨벡스 최적화에 포함된다
컨벡스 최적화는 컨벡스 함수를 대상으로 최소화 하는 작업으로 정의된다.
그런데 컨케이브 함수 최대화도 컨벡스 최적화로 볼 수 있다.
컨케이브 함수를 반대로 뒤집으면 컨벡스 함수와 같다.
그리고 컨케이브 함수의 최대점은 이 함수를 반대로 뒤집은 컨벡스 함수의 최소점과 같다.
$\Rightarrow$ 컨케이브 함수 최대화 문제와 컨벡스 함수 최소화 문제 둘 중 하나를 풀 수 있으면 나머지 하나도 반드시 풀 수 있다.
결국 컨케이브 함수 최대화 문제를 푸는 건 컨벡스 함수 최소화 문제 푸는 것과 같다.
$\Rightarrow$ 컨케이브 함수 최대화 문제를 푸는 것 $=$ 컨벡스 최적화 문제
따라서 컨케이브 함수 최대화도 컨벡스 최적화에 포함되는 개념이다.
$Maximize(concave), Minimize(convex) \subset$ $Convex$ $Optimization$
한편
대부분의 경우 최적화 할 때 최소화 문제만을 고려한다. 최소화 문제를 풀 수 있으면 최대화 문제도 풀 수 있다.
그러면 사실상 컨벡스 최적화 문제 $= Minimize(Convex)$ 를 의미한다고 볼 수 있다.
그래서 컨벡스 최적화를 다음과 같이 정의하기도 한다.
$\frac{d^{2}h}{dx^{2}} \ge 0$
‘목적함수의 2차 도함수가 0 이상인 구간 에서만 정의된 최적화(최소화)’
다변수함수의 경우
$x^{T}Hx \ge 0$
‘목적함수의 헤시안 행렬(2차 도함수 행렬)이 양의 준정부호인 영역 에서만 정의된 최적화(최소화)’
즉, 목적함수 $h$의 볼록구간(영역)에서만 정의된 최적화(최소화)라는 것이다.
전역 최적화 문제를 푸는 도구로서의 컨벡스 최적화
# 목적함수가 전역 최저점 뿐 아니라, 국소 최저점이 여러 개 있는 경우
위에서 봤던 비선형 목적함수를 다시 보자.

국소최저점이 많아서 전역 최적화에 실패했었다.
이 함수의 각 볼록구간만 잘라서, 각각 최적화 하는 것은 컨벡스 최적화를 3번 하는 것과 같다.
우선 위 비선형 목적함수에서 2차도함숫값이 항상 0 이상인 구간만 구해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def f_non_linear(x) :
return x**2-20*np.cos(x)
x = sympy.symbols('x')
f = x**2-20*sympy.cos(x)
fprime = sympy.diff(f)
sympy.diff(fprime)
def h(x) :
return 20*np.cos(x)+2
x = np.arange(-10,10,0.2)
result = np.array([x for x in x if h(x) >= 0 ])
plt.plot(result, f_non_linear(result), 'ro-')
first_convex = result[result < -4]
second_convex = result[(result > -2) & (result < 2)]
third_convex = result[result > 4]

빨간색 점으로 표현된 3개 구간이 2차 도함수가 항상 0 이상인 컨벡스 구간이다.
각 구간별로 컨벡스 최적화해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 구간1
plt.plot(first_convex, f_non_linear(first_convex))
plt.title('2차 도함수 >= 0 인 첫번째 컨벡스 구간(볼록구간)')
mu = 0.03
# 최적화 시작점
a = -7.5
for i in range(50) :
plt.plot(a,f_non_linear(a), 'go', markersize=5)
next_ = a - mu*gradient(a)
a = next_
print(f'컨벡스 구간 1의 최소점 : {f_non_linear(a)}')
print(f'컨벡스 구간 1의 최적해 : {a}')

구간 1 최소점 : 15.79
구간 1 최적해 : -5.67
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 구간2
plt.plot(second_convex, f_non_linear(second_convex))
plt.title('2차 도함수 >= 0 인 두번째 컨벡스 구간(볼록구간)')
mu = 0.06
# 최적화 시작점
a = second_convex[3]
for i in range(10) :
plt.plot(a,f_non_linear(a), 'go', markersize=5)
next_ = a - mu*gradient(a)
a = next_
print(f'컨벡스 구간 2의 최소점 : {f_non_linear(a)}')
print(f'컨벡스 구간 2의 최적해 : {a}')

구간 2 최소점 : -19.99
구간 2 최적해 : -4.512
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 구간3
plt.plot(third_convex, f_non_linear(third_convex))
plt.title('2차 도함수 >= 0 인 세번째 컨벡스 구간(볼록구간)')
mu = 0.06
# 최적화 시작점
a = third_convex[10]
for i in range(10) :
plt.plot(a,f_non_linear(a), 'go', markersize=5)
next_ = a - mu*gradient(a)
a = next_
print(f'컨벡스 구간 3의 최소점 : {f_non_linear(a)}')
print(f'컨벡스 구간 3의 최적해 : {a}')

구간 3 최소점 : 15.79
구간 3 최적해 : 5.67
이렇게 각각 컨벡스 구간별로 컨벡스 최적화를 3번 할 수 있다.
한편, 컨벡스 최적화를 하면 각 구간 별 전역 최적해 값을 얻을 수 있다.
위 경우에도 구간 1~3의 전역 최적해 값을 얻을 수 있었다.
각 구간의 전역 최적해 값은 함수 전체로 보면 국소 최저점들일 수 있다.
이 국소 최저점들을 비교했을 때, 가장 작은 값이 전역 최적점이라고 볼 수 있다.
컨벡스 구간 2의 최소위치가 가장 출력값이 작으므로, 전역 최소점이라고 볼 수 있다.
$\Rightarrow$ 이렇게 전역 최적화가 어려운 비선형 목적함수를,
여러 컨벡스 구간으로 잘라서 컨벡스 최적화 한 다음
각 결과값을 비교해서 전역 최적점을 찾아낼 수도 있다.
따라서 컨벡스 최적화는 전역 최적화 문제를 푸는 도구가 될 수 있다.
파이썬 패키지로 컨벡스 최적화 하기
CVXPY
목적함수와 최적화 문제 모두 DCP rule 을 만족해야 컨벡스 최적화 가능한 패키지.
- 목적함수가 비록 컨벡스(컨케이브) 함수라도 DCP rule 에 안 맞으면 최적화 못한다.
- 목적함수가 DCP rule 에 부합해도, 정의한 최적화 문제가 DCP rule 에 안 맞으면 최적화 못 한다.
- 직관적 심볼릭 연산 할 수 있다는 장점. 있다.
CVXOPT
- solvers 객체를 이용해서 다양한 컨벡스 최적화가 가능하다.
- 주로 LP문제(선형계획법 문제), QP문제(이차계획법 문제) 해결을 위해 CVXOPT를 사용했다.
CVXPY
목적함수와 최적화 문제 모두 DCP rule 을 만족해야 컨벡스 최적화 가능한 패키지.
- (강조) 목적함수가 비록 컨벡스(컨케이브) 함수라도 DCP rule 에 안 맞으면 최적화 못한다.
- (강조) 목적함수가 DCP rule 에 부합해도, 정의한 최적화 문제가 DCP rule 에 안 맞으면 최적화 못 한다.
- 컨벡스 최적화 할 때 등식/부등식 제한조건을 걸 수도 있다.
최적화 하려는 목적함수가 DCP rule 만족하는지 보려면
object.curvature 명령 입력했을 때 CONVEX, CONCAVE, AFFINE, CONSTANT 로 나오는 목적함수들은 모두 DCP rule 만족하는 것들이다.
*Constant 와 Affine 은 Concave 이기도 하고 Convex 이기도 하다. 따라서 Constant 와 Affine 도 컨벡스 최적화 할 수 있다(컨벡스 함수다).
1
object.curvature
내가 정의한 최적화 문제가 DCP rule 만족하는지 보려면
1
2
3
4
5
# 목적함수 최대화, 최소화 명령이 dcp rule 만족하는가
object.is_dcp()
# 제한조건 반영한 최적화 문제가 dcp rule 만족하는가
prob.is_dcp()
*참고
컨벡스 함수를 최대화 하라고 한다던가, 컨케이브 함수를 최소화 하라고 한다던가,
혹은 목적함수에 제한조건을 적용했을 때 최대화 또는 최소화가 불가능한 경우
최적화 문제가 DCP rule 위반이 된다.
CVXPY 컨벡스 최적화 코드 예시
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import cvxpy as cp
a = cp.Variable()
b = cp.Variable() # 심볼릭 변수 지정
# 목적함수 지정
obj2 = cp.Minimize(a+b)
# 제한조건
const = a**2+b**2 == 1
# 최적화 문제 정의
prob = cp.Problem(obj2, constraints=[const])
# 문제 풀어라는 명령
prob.solve()
CVXPY로 직접 컨벡스최적화 해보자
만약 목적함수가 DCP rule 만족하지 않는 경우
다음과 같은 에러 메시지가 뜬다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# DCP rule 만족하지 않는 경우
import cvxpy as cp
a = cp.Variable()
b = cp.Variable()
# 목적함수
obj2 = cp.Minimize(a+b)
# 제한조건
const = a**2+b**2 == 1
# 최적화문제 정의
prob = cp.Problem(obj2, constraints=[const])
prob.solve()

위 경우에는
우선 목적함수 obj2 는 $affine$ 이다. 컨벡스 최적화 가능하다.
하지만, 제한조건 $const$ 를 반영한 최적화 문제가 DCP rule 에 어긋나기 때문에 에러가 발생한 것이다.
즉, 제한조건 하에서 목적함수 최소화 문제 푸는 게 불가능하다는 말이다.
라그랑주 승수법으로 제한조건 최적화 목적함수를 직접 구해보면, 가능한 $\lambda$ 값이 두개가 나온다.
$\lambda = \frac{\sqrt(2)}{2}$ or $-\frac{\sqrt(2)}{2}$
$\Rightarrow$
$h_{1} = x_{1}+x_{2} + \frac{\sqrt{2}}{2} (x_{1}^{2}+x_{2}^{2}-1)$
$h_{2} = x_{1}+x_{2}-\frac{\sqrt{2}}{2} (x_{1}^{2}+x_{1}^{2}-1)$
위 $h_{1}, h_{2}$ 가 가능한 두가지 목적함수다.
각 목적함수를 시각화해보면 아래와 같다.
$h_{1}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
xx = np.linspace(-50,50,500)
yy = np.linspace(-50,50,500)
X,Y = np.meshgrid(xx,yy)
def h1(x, y) :
return x+y+(np.sqrt(2)/2)*(x**2+y**2-1)
Z1 = h1(X,Y)
def h2(x,y) :
return x+y-(np.sqrt(2)/2)*(x**2+y**2-1)
Z2 = h2(X,Y)
ax = plt.gca(projection='3d')
ax.plot_surface(X,Y,Z1, linewidth=0.03, cmap='flare_r')
plt.title('1')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

$h_{2}$
1
2
3
4
5
6
ax = plt.gca(projection='3d')
ax.plot_surface(X,Y,Z2, linewidth=0.03, cmap='terrain')
plt.title('2')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
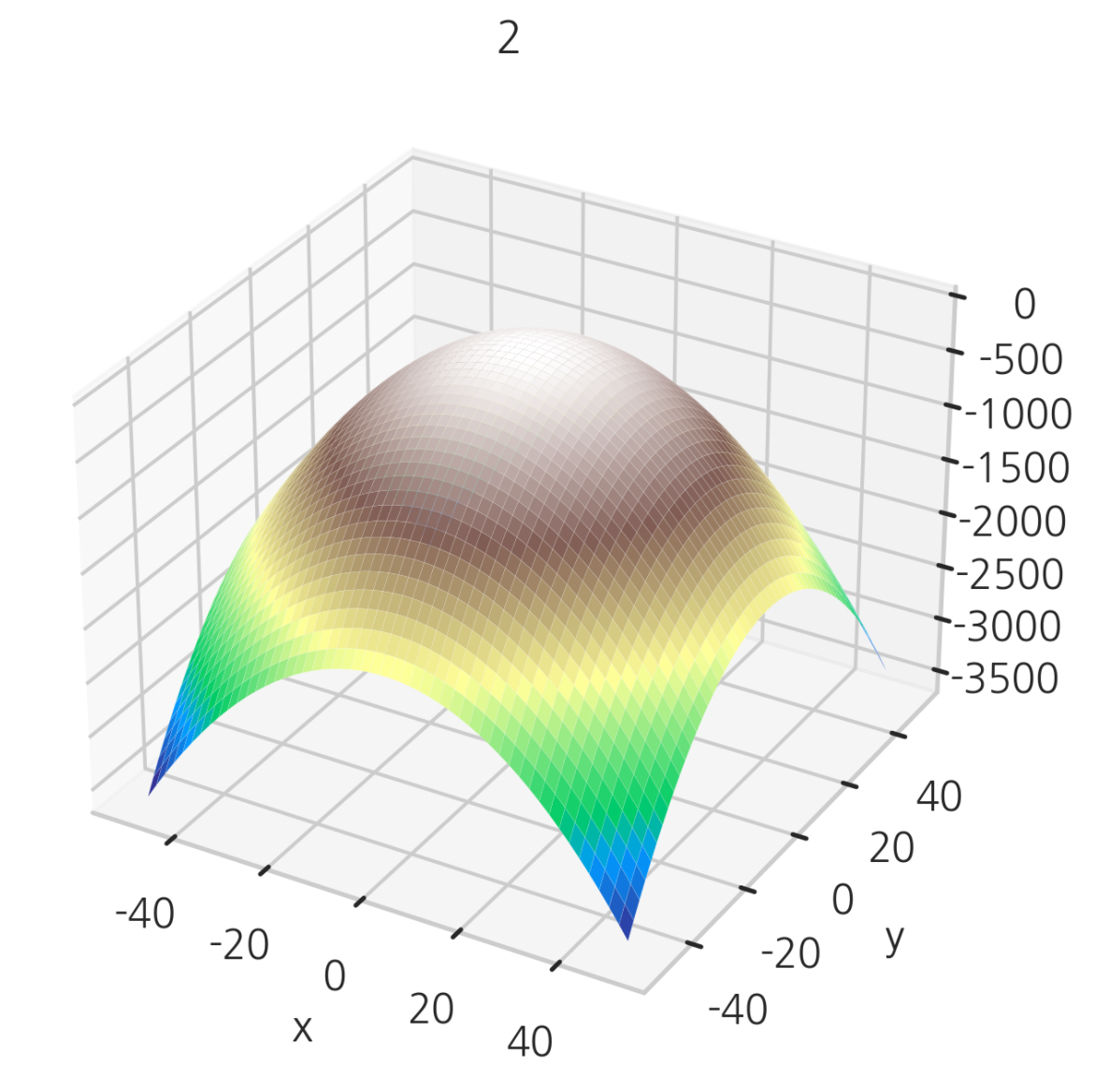
$h_{2}$ 은 $h_{1}$ 를 반대로 엎어놓은 모양이다.
여기서 핵심은,
주어진 제한조건
$x_{1}^{2}+x_{2}^{2} = 1$ 이 최적해에 미치는 영향을 반영해 목적함수를 라그랑주 승수법써서 변형하면서
가능한 목적함수의 경우가 두 가지 나온다는 것이다.
두 가지 경우 중 $h_{2}$ 는 concave 함수로, 최소화 연산이 불가능하다.
사이파이 optimize.minimize 명령을 이용해도 마찬가지였다.
1
2
3
4
def h1(x) :
return x[0]+x[1]+(np.sqrt(2)/2)*(x[0]**2+x[1]**2-1)
sp.optimize.minimize(h2, np.array([0,0]))

그래서 DCP rule 위반이라고 에러 메시지가 발생한 것이었다.
제한조건을 반영한 목적함수 $h_{1}$ 만 가지고 최소화 연산을 시도했다.
$h_{1}$ 함수는 컨벡스 함수로, 최소화 연산이 가능할 것이었다.
1
2
3
4
5
6
7
8
9
10
11
12
13
# 컨벡스 최적화 1
import cvxpy as cp
x = cp.Variable()
y = cp.Variable()
# 목적함수
h = cp.Minimize(x+y+(np.sqrt(2)/2)*(x**2+y**2-1))
# 최적화 문제 정의
prob = cp.Problem(h)
prob.solve()
x.value, y.value

원하는 대로 최소화 연산 할 수 있었다.
한편, $h_{2}$ 는 최대화 연산은 가능할 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
# 컨벡스 최적화 2
import cvxpy as cp
x = cp.Variable()
y = cp.Variable()
# 목적함수
h = cp.Maximize(x+y-(np.sqrt(2)/2)*(x**2+y**2-1))
# 최적화 문제 정의
prob = cp.Problem(h)
prob.solve()
x.value, y.value

예상대로 최대화 할 수 있었다.
그러면 이제, DCP rule 만족하는 경우에 대해, CVXPY 로 컨벡스최적화를 해보자.
- 심볼릭연산이다.
예1 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 컨벡스 최적화 테스트 2
import cvxpy as cp
x = cp.Variable()
y = cp.Variable()
f = (x-2)**2+2 # convax 함수인지, concave 함수인지 자동으로 인식한다.
print(f.curvature) # 함수가 convex 인지, concave 인지, affine 인지, constant 인지 알려주는 명령
# 목적함수
obj = cp.Minimize(f)
print(obj.is_dcp())
# 최적화 문제의 정의
prob = cp.Problem(obj)
print(prob.is_dcp())
print(prob.solve())
print(x.value)
결과 :
CONVEX
True
True
2.0
2.0
단변수함수이면서 컨벡스 함수인 $(x-2)^{2}+2$ 를 CVXPY 로 최적화 했다.
예2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 컨벡스 최적화 테스트 3
x = cp.Variable()
y = cp.Variable()
f = x**2+y**2
print(f.curvature)
obj = cp.Minimize(f)
constraints = [x+y-1==0]
prob = cp.Problem(obj, constraints=constraints)
print(prob.is_dcp()) # 목적함수, 제약조건 종합 고려해서. 목적함수 최소화가 가능한가.
print(prob.solve());print(x.value, y.value)
결과 :
CONVEX
True
0.5
0.5
2차원 다변수함수인 $x^{2}+y^{2}$ 를 CVXPY로 컨벡스최적화 했다.
물론 함수는 컨벡스함수다.
제한조건은 $x+y-1=0$ 등식제한조건을 줬다.
예3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 컨벡스 최적화 테스트 4
x = cp.Variable()
y = cp.Variable()
obj = cp.Minimize(x**2+y**2)
constraints = [
x+y-1 <= 0
]
prob = cp.Problem(obj, constraints)
print(prob.is_dcp())
print(prob.solve(), x.value, y.value)
결과 : True, 0, 0, 0
같은 2차원 다변수함수에 대해 이번에는
$x+y-1$ <= $0$ 부등식제한조건을 줬다.
예 4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 컨벡스 최적화 테스트 6
x = cp.Variable()
y = cp.Variable()
obj = cp.Minimize((x-4)**2+(y-2)**2)
print(obj.is_dcp())
constraints = [
x+y-1 <= 0 ,
-x+y-1 <= 0 ,
-x-y-1 <= 0 ,
x-y-1 <= 0
]
prob = cp.Problem(obj, constraints = constraints)
print(prob.is_dcp())
prob.solve(), x.value, y.value
True, True,
(13.0, array(1.), array(-1.11022189e-22))
이번 시도는 2차원 다변수함수 $(x-4)^{2}+(y-2)^{2}$ 를 가지고 최소화 문제를 풀었다.
목적함수는 컨벡스 함수다.
제한조건은 부등식제한조건 4개를 동시에 줬다.
CVXOPT
CVXPY 처럼, 컨벡스최적화 패키지다.
LP 문제, QP 문제 등을 비롯해 다양한 컨벡스 최적화가 가능했다.
- ndarray 객체를 CVXOPT matrix 자료형으로 변환해서 넣어야 한다.
- 모든 스칼라 값은 부동 소숫점 실수 형태로 바꿔서 넣어야 한다.
나는 이 패키지를 LP 문제와 QP 문제 해결을 위해 사용했다.
LP 문제와 QP 문제는 뒤에서 다시 정리할 것이다.
CVXOPT 로 LP문제 해결하기
1
2
3
4
5
6
# cvxopt로 선형계획법 풀기
c = matrix(np.array([-3.0,-5.0]))
A = matrix(np.array([[-1.0,0.0],[0.0,-1.0],[1.0,2.0],[4.0,5.0]]))
b = matrix(np.array([-100.0, -100.0, 500.0, 9800.0]))
np.array(solvers.lp(c, A, b)['x'])

CVXOPT 로 QP문제 해결하기
QP 문제의 목적함수 - 일반화된 이차형식 - 이 컨벡스함수인 경우만 최적화 할 수 있다.
- 일반화된 이차형식의 행렬 $Q$ 가 양의 준정부호 여야 한다.
- $Q$ 가 양의 준정부호가 아니면 넌 컨벡스 함수가 된다. 이 경우, solver.qp 명령으로 이차계획법 문제 못 푼다. 다른 방법 써야 한다.
1
2
3
4
5
6
7
8
9
10
# 이차계획법 문제
from cvxopt import matrix, solvers
Q = matrix(np.array([[2.0,0.0],[0.0,2.0]]))
c = matrix(np.array([0.0,0.0]))
A = matrix(np.array([[1.0,1.0]]))
b = matrix(np.array([1.0]))
r = solvers.qp(Q,c,A=A,b=b)['x']
np.array(r)
array([[0.5], [0.5]])
제한조건 있는 최적화 문제
1. 등식 제한조건이 있는 최적화 문제
최적해가 목적함수를 최소화 하면서도 $f_{i} = 0$ 꼴로 생긴
연립방정식(또는 1개 방정식) 을 동시에 만족해야 하는 경우,
‘등식 제한조건이 있는 최적화 문제’ 라고 한다.
(등식 제한조건은 $f = 0$ 형태여야 한다. )
등식 제한조건 있는 최적화 예)
목적함수
$f(x_{1}, x_{2}) = x_{1}^{2}+x_{2}^{2}$
등식 제한조건
$g(x_{1}, x_{2}) = x_{1}+x_{2}-1 = 0$
동시에 만족하는 최적해 $x$ 를 찾아라.
위 문제는 아래 그림에서 등고선과 붉은 직선이 만나는 벡터 $x$ 를 찾는 것과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
xx = np.linspace(-5,5,400)
yy = np.linspace(-5,5,400)
X, Y = np.meshgrid(xx,yy)
def f(x,y) :
return x**2+y**2
Z = f(X,Y)
def g(x) :
return -x+1
levels=np.flip([16, 4.8, 1.5, 0.5, 0.2])
ax = plt.contour(X,Y,Z, levels=levels, colors='gray')
plt.clabel(CS=ax)
plt.axis('equal')
plt.plot(xx, g(xx), 'r')
plt.plot(0,0,'rP')
plt.plot(0.5, 0.5, 'bo', ms=5)
plt.title('목적함수 $x^{2}+y^{2}$를 등식 제한조건 $x_{1}+x_{2}-1=0$ 을 걸고 최적화 ')
plt.xlim(-5,5)
plt.ylim(-5, 5)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

라그랑주 승수법
제한조건이 있는 최적화 문제는 라그랑주 승수법을 이용해서 풀 수 있다.
라그랑주 승수법에서는, 목적함수를 다음과 같이 변형한다.
$h = f(x) + \sum_{i}^{n}{\lambda_{i}g_{i}(x)}$
여기서
$g_{i}(x)$ 는 $i$ 번째 제한조건 (등식, 부등식)
$\lambda_{i}$ 는 $i$ 번째 제한조건의 라그랑주 승수
$f(x)$ 는 본래 목적함수
이다.
그리고 이처럼 변형된 목적함수 $h$ 를 사용해서 최적화 한다.
내가 찾는 최적해는 $h$ 의 그레디언트 벡터 $= 0$영벡터 만드는 $x_{1}, x_{2}, …x_{n}$ 값들이다.
- 라그랑주 승수는 고려하지 않는다.
라그랑주 승수의 의미
라그랑주 승수 $\lambda_{i}$ 는 ‘각 제한조건이 최적해에 미치는 영향의 크기’를 타나낸다.
- 만약 제한조건이 최적해에 아무 영향도 미치지 못하면, 그 제한조건의 라그랑주 승수 $\lambda_{i}$ 는 $0$ 이다.
위에서 풀었던 등식 제한조건 있는 최적화 문제를
라그랑주 승수법으로 풀어보자.
목적함수 : $f(x_{1}, x_{2}) = x_{1}^{2}+x_{2}^{2}$
등식 제한조건 : $g(x_{1}, x_{2}) = x_{1}+x_{2}-1 = 0$
였다.
목적함수 $f$ 를 라그랑주 승수 이용해서 $h$ 로 바꾸자.
$h = x_{1}^{2}+x_{2}^{2} + \lambda(x_{1}+x_{2}-1)$
이 목적함수 $h$의 그레디언트 벡터는
$\nabla{h} = [2x_{1}+\lambda, 2x_{2}+\lambda, x_{1}+x_{2}-1]^{T}$ 이다.
그레디언트 벡터 각 요소가 $0$ 되게 하는 $\lambda$ , $x_{1}$, $x_{2}$ 를 찾자.
$\lambda = -1, x_{1}=x_{2} = \frac{1}{2}$
이다. 따라서 붉은 직선 위 점이면서, 동시에 등고선 플롯 $z$ 값을 최소화 하는 최적해는 $[\frac{1}{2}, \frac{1}{2}]^{T}$ 다.

사이파이로 등식 제한조건 최적화 하기
사이파이의 fmin_slsqp() 명령을 사용하면
최소자승법 알고리듬을 사용해서 등식 제한조건이 있는 최적화 문제를 해결할 수 있다.
1
sp.optimize.fmin_slsqp(f_name, x_{0}, eqcons=[constraint1, constraint2,...])
- f_name : 최소화 할 함수 이름
- x_{0} : 최적화 시작점 (적당한 값 넣으면 된다)
- eqcons : 제한조건 함수 이름. 리스트 자료형 안에 넣어야 한다.
fmin_slsqp() 사용 예 )
1
2
3
4
5
6
7
# 위에서 라그랑주 승수법으로 풀었던 문제
def f(x) :
return x[0]**2+x[1]**2
def g(x) :
return x[0]+x[1]-1
sp.optimize.fmin_slsqp(f, (1,2), eqcons=[g])

부등식 제한조건 최적화 문제
부등식도 최적화 제한조건으로 걸 수 있다.
이 경우는 주어진 부등식을 만족하면서, 주어진 목적함수를 최소화 하는 최적해를 찾는 것이다.
연립부등식이 최적화 제한조건으로 제시된다.
$g_{j} \leq 0, (j = 1, 2, …M)$
(부등호 방향은 $g \leq 0$ 이어야 한다. )
부등식 제한조건 최적화 문제도 라그랑주 승수법으로 풀면 된다.
$h = f(x) + \sum_{1}^{n}{\lambda_{i}g_{i}(x)}$
등식 제한조건일 때랑 똑같이 변형된 목적함수 $h$ 를 만들면 된다.
한편, 등식 제한조건 최적화 문제의 최적화 필요조건은 ‘기울기 필요조건’ 이었다.
부등식 제한조건 최적화 문제의 최적화 필요조건은 ‘KKT 조건’ 이다.
최적해가 만족해야 하는 KKT 조건은 다음과 같다.
1. $\frac{\partial{h}}{\partial{x_{i}}} = 0$
목적함수 $h$ 를 $x_{i}$ 로 미분한 값은 모두 0 이어야 한다.
2. $\lambda_{i} * g_{i}(x) = 0$
$\lambda_{i}$ 또는 $g_{i}(x)$ 둘 중 하나는 반드시 0 이어야 한다.
(둘 다 0 일수도 있다)
3. $\lambda_{i} \ge 0$
모든 라그랑주 승수는 0 이상이어야 한다.
위 3 가지 조건 중 2번 조건만 먼저 만족시키면, 1. 3 번 조건은 자연스럽게 만족된다.
이 2번 조건에 의해 부등식 제한조건은 결국 등식 제한조건 문제 푸는 것과 같아진다.
case 1
$\lambda_{i} = 0$ 인 경우
$i$ 번째 부등식 제한조건이 최적해에 아무런 영향도 못 미친다는 의미다.
$\lambda_{i} = 0$ 이기 때문에, 목적함수 $h$ 에서 $i$ 번째 부등식 제한조건은 사라진다. ‘쓸모가 없다’.
case 2
$g_{i}(x) = 0$ 인 경우
$g_{i}(x) = 0$ 은 ‘등식 제한조건’ 이었다.
따라서 등식 제한조건의 $\lambda_{i}$ 도 0 되는 아주 특수한 경우를 제외하고는
제한조건 $g_{i}(x)$ 는 등식 제한조건과 같아진다.
따라서 목적함수 $h$ 를 가지고 등식 제한조건 최적화 문제를 풀면(기울기 필요조건 만족) 최적해를 구할 수 있다.
$\Rightarrow$ 결국 부등식 제한조건 최적화 문제는
등식 제한조건 최적화 문제 푸는 것과 같다.
부등식 제한조건 최적화 문제)
- 라그랑주 승수법으로 목적함수 변형
- (KKT 조건에 의해) 각 제한조건 없애거나. 등식으로 바꾼다.
- 기울기 필요조건으로 최적화 문제 푼다.
$\Rightarrow$ 제한조건 최적화 문제는 결국 모두 라그랑주 승수법, 기울기 필요조건으로 푼다.
부등식 제한조건 최적화 문제를 그림으로 그리면 다음과 같다.
다음은 목적함수가 $x^{2}+y^{2}$ 이고,
부등식 제한조건이 각각
$g_{1}(x_{1}, x_{2}) = x_{1}+x_{2}-1 \leq 0$
$g_{2}(x_{1}, x_{2}) = -x_{1}-x_{2}+1 \leq 0$
인 경우다. 따로따로 하나씩 적용했다.
부등식 제한조건이 $g_{1}$ 인 경우
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def f(x, y) :
return x**2+y**2
xx = np.linspace(-5,5,500)
yy = np.linspace(-5,5,600)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
plt.contour(X,Y,Z, levels=[0.5, 2,8], colors='k')
plt.axis('equal')
plt.ylim(-3,3)
plt.xlim(-5,5)
def con1(x) :
return -x+1
plt.plot(xx, con1(xx), c='r')
plt.fill_between(xx, -20, con1(xx), alpha=0.2)
plt.plot(0,0,'ro', markersize=10)
plt.text(-0.3, -0.5, '최적해')
plt.title('부등식 제한조건이 최적해 에 영향 미치지 못하는 경우')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

그림을 보면 이 부등식 제한조건(붉은 직선 아래 푸른색 영역) 은 최적해에 전혀 영향을 못 미치고 있다(쓸모없다).
라그랑주 승수의 의미는 ‘제한조건이 최적해에 미치는 영향의 크기’ 였다.
이 제한조건이 최적해에 전혀 영향 못 미치기 때문에, 라그랑주 승수 $\lambda_{1} = 0$ 일 것이다.
부등식 제한조건이 $g_{2} 인 경우$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def f(x, y) :
return x**2+y**2
xx = np.linspace(-5,5,500)
yy = np.linspace(-5,5,600)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
CS = plt.contour(X,Y,Z, levels=[0.5, 2,8], colors='k')
plt.clabel(CS)
plt.axis('equal')
plt.ylim(-3,3)
plt.xlim(-5,5)
def con2(x) :
return -x+1
plt.plot(xx, con2(xx), 'r')
plt.fill_between(xx, 20, con2(xx), alpha=0.3)
plt.plot(0.5, 0.5, 'ro', markersize=5)
plt.suptitle('부등식 제한조건이 최적해에 영향 미치는 경우', y = 1.0003)
plt.title('원래 최적해 : $[0,0]$, 바뀐 최적해 : $[0.5, 0.5]$')
plt.plot(0,0, 'bP')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

이 경우에는 부등식 제한조건이 최적해에 영향을 미치고 있다.
붉은 직선과 푸른색 영역이 부등식 제한조건이다.
부등식 제한조건 때문에 원래 $[0,0]$ 이었던 최적해가 $[0.5, 0.5]$ 로 바뀌었다.
이 경우에는 제한조건이 최적해에 영향을 미쳤기 때문에, $\lambda_{2} \ne 0$ 일 것이라 추측해볼 수 있다.
한편, 위 그림을 잘 보면 제한조건을 만족하는 최적해는 결국 붉은 직선 위의 점이다.
곧, 새로운 최적해는 부등식 제한조건 영역의 경계선에 걸린다는 말이다.
푸른색 영역이 뒤로 조금 후퇴해도, 제한조건을 걸면서 변화한 최적해(붉은 점)는 결국 푸른색 영역의 경계선인 붉은 선 위의 값이 될 것이다.
그러면 결국 원래 목적함수를 최소화 시키는 붉은 직선 위의 점 찾는 문제(= 등식 제한조건 문제) 가 된다.
따라서 그림으로도 부등식 제한조건이 결국
쓸모없거나,
등식 제한조건이 된다
는 사실을 확인할 수 있었다.
다음은 목적함수가 $(x_{1}-4)^{2} + (x_{2}-2)^{2}$ 이고, 부등식 제한조건이 $\sum_{i}^{2}\lvert x_{i} \rvert-1 \leq 0$ 인 최적화 문제를 그림으로 표현한 예다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def f(x, y) :
return np.sqrt((x-4)**2+(y-2)**2 )
xx = np.linspace(-2,5,500)
yy = np.linspace(-1.5,3,600)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
CS = plt.contour(X,Y,Z, colors='k', levels=np.arange(0.5, 5, 0.5)*np.sqrt(2))
x2 = np.linspace(-1,0,100)
x3 = np.linspace(0,1,100)
plt.fill_between(x2, x2+1, -x2-1, alpha=0.2, color='m')
plt.fill_between(x3, -x3+1, x3-1, alpha=0.2, color='m')
plt.plot(1,0,'ro', markersize=10)
plt.xlabel('$x_{1}$')
plt.ylabel('$x_{2}$')
plt.title('부등식 제한조건 최적화 문제')
plt.plot(np.linspace(-1,2),np.linspace(-1,2)-1, 'r', alpha=0.2)
plt.plot(np.linspace(-1,2),-np.linspace(-1,2)+1, 'r', alpha=0.2)
plt.show()

원래 $[2,4]$ 였던 최적해가 부등식 제한조건 때문에 변해서 붉은 점 $[1,0]$이 됬다.
붉은 점은 위 그림에서 교차하는 두 붉은 직선 상에 동시에 위치한 점이다.
즉, 붉은 점은 붉은 두 개 직선이 속한 두 개의 부등식 제한조건 영역 경계에 위치해 있다.
$\Rightarrow$ 두 직선을 포함하는 두 개 부등식 제한조건 영역들은 모두 등식 제한조건으로 바뀔 것이다.
나머지 두 개 부등식 제한조건은 붉은 점에 전혀 영향 못 미치고 있다.
따라서 보라색 마름모의 나머지 두 변을 포함하는 왼쪽 두 개 제한조건들은 할당된 라그랑주 승수 $\lambda_{i}$ 값이 $0$ 일 것이다(쓸모없음).
사이파이로 부등식 제한조건 있는 함수 최적화 하기
등식 제한조건 최적화 할 때 사용했던 fmin_slsqp 명령을 다시 쓸 수 있다.
fmin_slsqp 명령은 ieqcons= 라는 argument 로 부등식 제한조건 함수를 받는다.
1
sp.optimize.fmin_slsqp(함수이름, 최적화시작점, ieqcons=[부등식제한조건 함수이름])
*부등식 제한조건을 ieqcons argument 에 넣을 때는 부등호 방향을 $\ge$ 이 되게 해서 넣어야 한다.
위 예제를 사이파이로 최적화 해보자.
1
2
3
4
5
6
7
def f(x) :
return np.sqrt((x[0]-4)**2+(x[1]-2)**2)
def ieqcons(x) :
return -np.sum(np.abs(x))+1
sp.optimize.fmin_slsqp(f, np.array([0,0]), ieqcons=[ieqcons])

데이터사이언스 스쿨 5.2.3 연습문제 )
위 예제 문제에서 제한조건을 다음과 같이 바꾼다.
$g(x) = \lvert x_{1} \rvert$ + $\lvert x_{1} \rvert - k = \sum_{i}^{2}{\lvert x_{i}\rvert}-k \leq 0$
$k$ 를 0.1 부터 10까지 변화시키면서, 최적화 해가 어떻게 바뀌는지 살펴봐라.
나의 답 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 5.2.4 연습문제
def f(x, y) :
return np.sqrt((x-4)**2+(y-2)**2 )
xx = np.linspace(-2,5,500)
yy = np.linspace(-1.5,3,600)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
plt.contour(X,Y,Z, colors='k', levels=np.arange(0.5, 5, 0.5)*np.sqrt(2))
c = 0
colors=['r', 'g', 'b', 'c', 'm', 'k', 'y']
for k in np.linspace(0.1, 10, 7) :
x1 = np.linspace(-k, 0)
x2 = np.linspace(0, k)
plt.fill_between(x1, x1+k, -x1-k, alpha=0.1, color=colors[c])
plt.fill_between(x2, -x2+k, x2-k, alpha=0.1, color=colors[c])
c+=1
plt.xlim(-2,5)
plt.ylim(-1.5, 3)
plt.suptitle('$k$ 가 변하면서, 최적화 해에 영향 미치는 부등식 제한조건도 변한다', y=1.0004)
plt.title('$k$가 일정 정도 이상 커지면 모든 부등식 제한조건이 최적화 해에 영향 못 미친다')
plt.show()

겹쳐진 여러 마름모가 변화된 $k$ 를 입력받은 부등식 제한조건 영역이다.
원래 최적해는 $[4,2]$ 였다.
보면 $k$ 가 일정 정도 이상 커지면, 4개 부등식 제한조건 모두 최적화 해에 영향 못 미친다는 사실을 관찰할 수 있었다.
(부등식 제한조건 영역이 최적해 $[4,2]$ 를 포함해 버린다)
더 자세히 보면
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
index = 0
def f(x, y) :
return np.sqrt((x-4)**2+(y-2)**2 )
colors=['r', 'g', 'b', 'c', 'm', 'k', 'y']
k = np.linspace(0.1, 10, 7)
xx = np.linspace(-2,5,500)
yy = np.linspace(-1.5,3,600)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
plt.contour(X,Y,Z, colors='k', levels=np.arange(0.5, 5, 0.5)*np.sqrt(2))
plt.xlim(-2,5)
plt.ylim(-1.5, 3)
x1 = np.linspace(-k[index], 0)
x2 = np.linspace(0, k[index])
plt.fill_between(x1, x1+k[index], -x1-k[index], alpha=0.1, color=colors[index])
plt.fill_between(x2, -x2+k[index], x2-k[index], alpha=0.1, color=colors[index])
plt.title(f'$k = {k[index]}$ 인 경우')
plt.plot(0.1, 0, 'ro',markersize=2)
plt.show()





이런식으로 변화한다. $k$ 가 커질 수록 부등식 제한조건 영역이 원래 최적해 $[4,2]$ 가까이 간다는 사실을 관찰할 수 있었다.
또
$k = 6.7$ 일 때는 본래 최적해가 부등식 제한조건 영역 안에 완전히 포함되었다. 곧, 부등식 제한조건이 더 이상 최적해에 영향 미치지 못했다 $\lambda_{i} = 0$
한편
부등식 제한조건을 감안한 최적해를 $[x_{1}, x_{2}]$ 라고 보고, $k$값이 변화할 때(부등식 제한조건이 변할 때) 이 벡터의 $x$ 좌표와 $y$ 좌표 값이 어떻게 변해가는지도 그래프로 나타내 봤다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def ieq_constraint(x) :
return -np.sum(np.abs(x))+k
def f(x) :
return np.sqrt((x[0]-4)**2+(x[1]-2)**2)
x1 = []
x2 = []
for k in np.linspace(0.1, 10, 100) :
result = sp.optimize.fmin_slsqp(f, np.array([1,1]), ieqcons=[ieq_constraint], iprint=0)
x1.append(result[0])
x2.append(result[1])
plt.plot(np.linspace(0.1,10,100), x1, label='$x_{1}$의 최적해')
plt.plot(np.linspace(0.1,10,100), x2, ls=':', c='g', label='$x_{2}$의 최적해')
plt.legend()
plt.xlabel('$k$')
plt.ylabel('$x_{i}$')
plt.title('$k$값 변화에 따른 $x_{1}, x_{2}$ 최적해 변화')
plt.show()
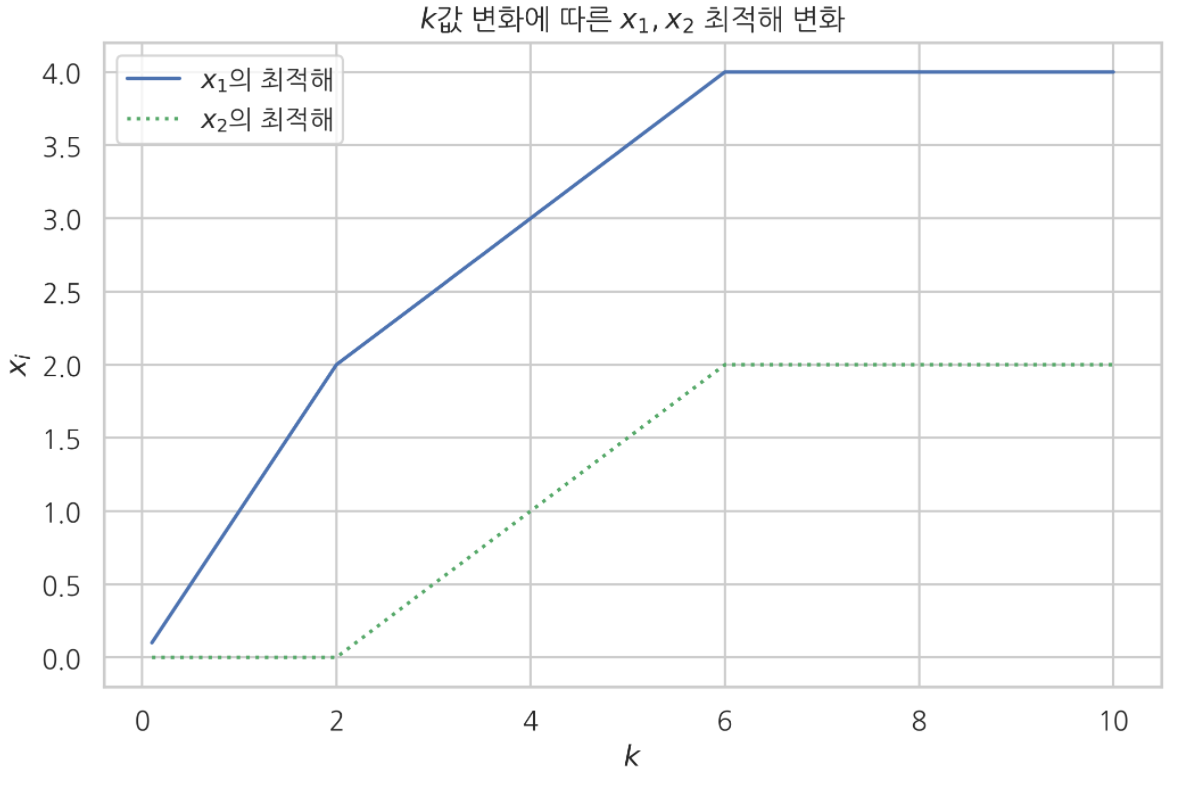
보면 $k$ 값이 커지면서 $x_{1}$, $x_{2}$ 값도 함께 커져감을 관찰할 수 있다.
그리고 $k = 6$ 에 도달했을 때 부터는 $x_{1}, x_{2}$ 도 더 이상 변화하지 않았다.
