‘프로그래머가 알아야 할 알고리즘 40’(임란 아마드 지음, 길벗 출판사) 을 통해 그래프 기본 개념, 그래프 분석 이론 기초를 공부. 복습하고나서, 그 내용을 내 언어로 바꾸어 기록한다.
그래프 알고리듬 - 1
그래프 알고리듬은 주로 효율적인 검색 알고리듬으로 쓰인다.
그래프 정의
정점(vertex)과 간선(edge) 집합.
- 간선은 두 정점 사이 ‘관계’ 나타낸다.
파이썬 networkx 라이브러리 사용해서 그래프 표현하기
빈 그래프 생성
1
2
3
4
# 빈 그래프 생성
import networkx as nx
g = nx.Graph()
그래프에 정점 1개 추가
1
2
# 정점 추가
g.add_node('mike')
그래프에 정점 여러 개 한번에 추가
1
2
# 정점 여러 개 한번에 추가
g.add_nodes_from(['amine', 'wasim', 'nick'])
두 정점 사이 간선 추가
1
2
# mike 정점과 amine 정점 사이 간선(관계) 추가
g.add_edge('mike', 'amine')
그래프 정점 목록 출력
1
2
# 그래프 정점 목록
list(g.nodes)
[‘mike’, ‘amine’, ‘wasim’, ‘nick’]
그래프 간선 목록
1
2
# 그래프 간선 목록
list(g.edges)
[(‘mike’, ‘amine’)]
아직 추가 안 된 정점에 대해서 간선 생성하기; 결과로 정점도 자동 생성된다.
1
2
3
4
5
# 아직 추가 안 된 정점에 대해 간선 생성하기 --> 결과로 imran 정점도 같이 생성된다.
g.add_edge('amine', 'imran')
print(list(g.edges))
print(list(g.nodes))
[(‘mike’, ‘amine’), (‘amine’, ‘imran’)]
[‘mike’, ‘amine’, ‘wasim’, ‘nick’, ‘imran’]
그래프 4 가지 유형
- 무방향 그래프
- 방향 그래프
- 무방향 멀티그래프
- 방향 멀티그래프
간선에 방향이 있으면 ‘방향’, 없으면 ‘무방향’ 그래프. 방향이 있는 경우 관계에 위계가 있는 것, 무방향이면 위계가 없다.
두 노드 사이 간선이 2개 이상이면 ‘멀티그래프’.
특수한 유형의 간선(edge) 2 가지
- 셀프 간선(엣지): 자기자신에게 다시 연결된 간선.
- 하이퍼 간선(엣지): 3개 이상 노드에 연결된 간선. 그래프에 하이퍼 간선이 1개 이상 존재하면, 그 그래프를 ‘하이퍼 그래프’ 라고 부른다.
에고 중심 네트워크
정의
특정 중심정점과 그 이웃들로 이루어진 네트워크.
- 중심정점을 ‘에고’라고 한다.
- 에고에 바로 인접한 정점들을 ‘알터(alter)’ 라고 한다.
- ‘그 이웃들’ 은 에고에 바로 인접한 정점들만 의미할 수도 있고, n개 엣지 만큼 떨어진 이웃들까지 의미할 수도 있다. 핵심은 중심정점 ‘에고’를 중심으로 한 네트워크 라는 것이다.
네트워크 분석 이론
주요 기본 용어 정리
경로
시작점과 끝점 사이 정점 집합.
- ‘집합’ 이기 때문에, 경로 내 중복된 정점은 있을 수 없다.
경로 길이
엣지(간선) 개수
최단 경로
여러 경로 중 엣지 수가 가장 적은, 경로.
삼각형 그래프
세 개 정점이 세 개 엣지로 연결된 그래프.
- 삼각형 그래프에서 각 정점은 서로 밀접한 ‘관계’를 맺고 있다. 세 정점이 서로 모두 연결되어 있기 때문이다.
네트워크 밀도
$density =\frac{Edges_{observed}}{Edges_{total}}$
주어진 네트워크에서 실제로 목격된 엣지 수와, 주어진 네트워크가 완전 연결 네트워크 일 때 가질 수 있는 최대 엣지 수 비율.
삼각형 그래프처럼, 각 정점이 서로 모두 엣지로 연결되어 있는 네트워크를 완전 연결 네트워크(fully connected network) 라고 한다. 완전 연결 네트워크는 그 엣지 수가 ‘허용가능한 최대’다. $n$ 개 정점으로 구성된 완전 연결 네트워크의 엣지 수는 아래 공식을 통해 구할 수 있다.
$Edges_{total} = \frac{n(n-1)}{2}$
- 밀도의 최댓값은 $1$ 이다.
정점 중심성 지표
중심성 지표 = 정점 중요도(가중치).
정점 중심성 지표로 사용할 수 있는 주요 지표로 아래 4가지가 있다.
1. 도수 중심성(degree centrality)
도수(degree): 특정 정점에 연결된 엣지(간선) 수.
정점 도수가 높을 수록(=정점에 연결된 엣지 수가 많을 수록), 중요한 정점이라고 간주한다.
정점의 도수 중심성은 아래 간단한 공식으로 계산한다.
$C_{dc_{a}} = \frac{degree_{a}}{\vert{V}\vert-1}$
- $degree_{a}$ : 정점 $a$ 도수
- $\vert{V}\vert$ : 그래프 총 정점 수
2. 매개 중심성(betweeness centrality)
특정 정점이 다른 정점들 사이에 끼어있는 정도.
$C_{betweeness_{a}} = \frac{n_{shortest_{a}}}{n_{shortest_{total}}}$
- $n_{shortest_{a}}$ : 모든 정점 페어 간 최단경로 중 정점 $a$ 를 지나는 최단경로 갯수
- $n_{shortest_{total}}$ : 모든 정점 페어 간 최단경로 총 갯수
3. 공정성과 근접 중심성
공정성: 자기자신과 그래프 내 다른 모든 정점과의 최단 경로 길이 총합.
$\Rightarrow$ $\sum_{j=1}^{n}{shortest_{a-j}}$
근접중심성: 공정성의 역수. 즉 $\frac{1}{\sum_{j=1}^{n}{shortest_{a-j}}}$
4. 고유벡터 중심성(eigenvector centrality)
정점 중심성 지표 계산하기
임의로 그래프 만들어서, 정점 별 중심성 지표(정점 별 중요도) 계산해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
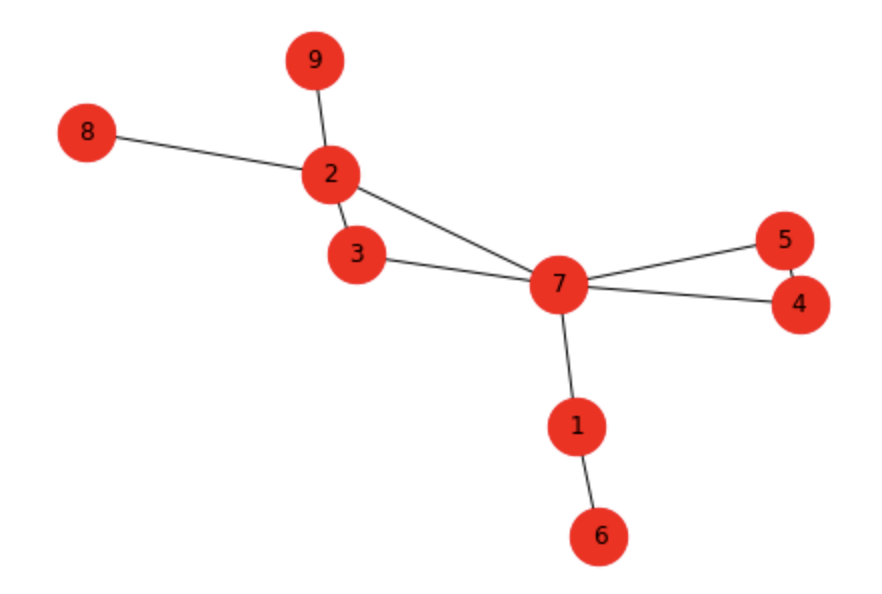
# networkx 라이브러리 사용해 예시 네트워크 생성
import networkx as nx
import matplotlib.pyplot as plt
# 10개 정점
vertexes = range(1,10)
# 간선
edges = [(7,2), (2,3), (7,4), (4,5), (7,3), (7,5), (1,6), (1,7), (2,8), (2,9)]
# 빈 그래프 생성
g = nx.Graph()
# 정점 10개 빈 그래프에 추가
g.add_nodes_from(vertexes)
# 간선 빈 그래프에 추가
g.add_edges_from(edges)
# 정점과 간선 추가된 그래프 시각화
nx.draw(g, with_labels=True, node_color='r', node_size=800)
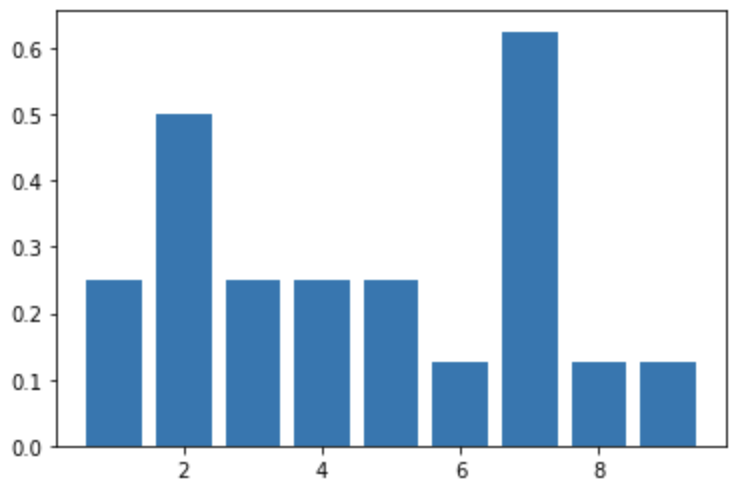
1 도수 중심성 지표 계산
1
2
3
4
5
6
# 도수 중심성 지표 계산
# 1. 도수 중심성 지표 계산
nx.degree_centrality(g)
# 시각화
plt.bar(nx.degree_centrality(g).keys(), nx.degree_centrality(g).values())
{1: 0.25, 2: 0.5, 3: 0.25, 4: 0.25, 5: 0.25, 6: 0.125, 7: 0.625, 8: 0.125, 9: 0.125}
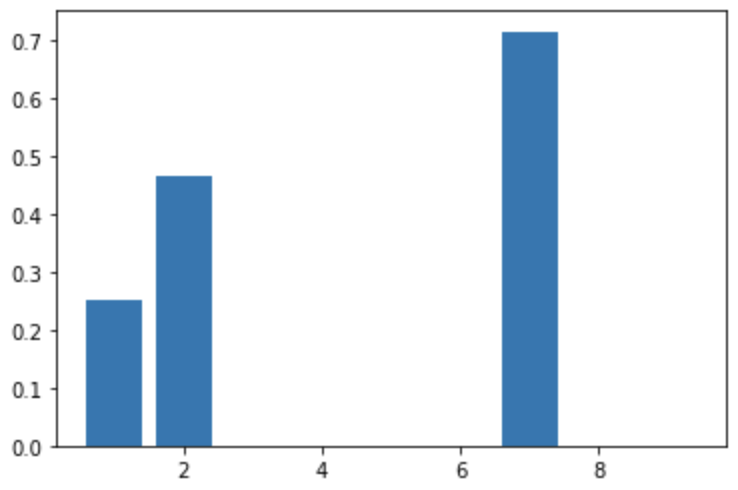
2 매개 중심성 지표 계산
1
2
3
4
# 2. 매개 중심성
print(nx.betweenness_centrality(g))
# 시각화
plt.bar(nx.betweenness_centrality(g).keys(), nx.betweenness_centrality(g).values())
{1: 0.25, 2: 0.46428571428571425, 3: 0.0, 4: 0.0, 5: 0.0, 6: 0.0, 7: 0.7142857142857142, 8: 0.0, 9: 0.0}
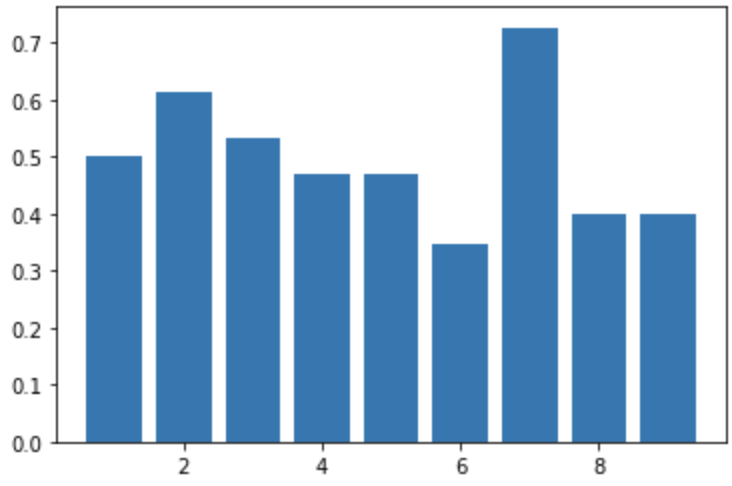
3 근접 중심성 지표 계산
1
2
3
4
# 3. 근접중심성
print(nx.closeness_centrality(g))
# 시각화
plt.bar(nx.closeness_centrality(g).keys(), nx.closeness_centrality(g).values())
{1: 0.5, 2: 0.6153846153846154, 3: 0.5333333333333333, 4: 0.47058823529411764, 5: 0.47058823529411764, 6: 0.34782608695652173, 7: 0.7272727272727273, 8: 0.4, 9: 0.4}
4 고유벡터 중심성 지표 계산
1
2
3
4
5
6
# 고유벡터 중심성
centrality = nx.eigenvector_centrality(g)
print(sorted([(v, round(c, 2)) for v, c in centrality.items()]))
# 시각화
plt.bar(centrality.keys(), centrality.values())
[(1, 0.24), (2, 0.45), (3, 0.36), (4, 0.32), (5, 0.32), (6, 0.08), (7, 0.59), (8, 0.16), (9, 0.16)]
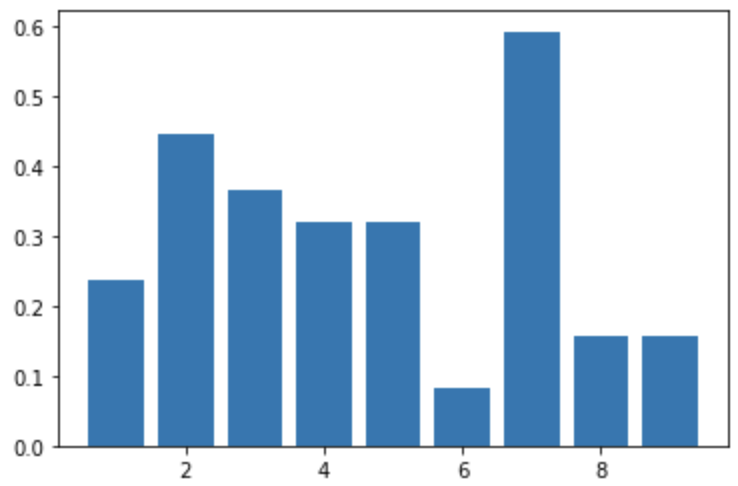
4 가지 중심성 지표에서, 정점 7이 항상 가장 높은 중심성 지표 기록했다.
$\Rightarrow$ 정점 7 중요도가 가장 높다. 정점 7이 그래프에서 가장 중요한 정점이다.
