그래프(Graph)
정의
객체 간 관계 나타내는 자료구조.
구성
종류
- 무방향그래프: 간선에 방향 없는 그래프
- 방향그래프: 간선에 방향 있는 그래프

- 완전그래프: 간선 수 최대인 그래프.

무방향그래프 경우 최대 간선 수: $\frac{n(n-1)}{2}$
방향그래프 경우 최대 간선 수: $n(n-1)$
그래프 정점과 간선
- 정점 A,B 를 연결하는 방향없는 간선: $(A,B)$ 로 표기
- 정점 A,B 연결하는 방향 있는 간선: $<A,B>$ 로 표기
- 무방향그래프에서는 간선 방향이 없기 때문에 $(A,B)$ 와 $(B,A)$ 는 같다.
- 방향그래프는 간선 방향이 있다. 따라서 $<A,B>$ 와 $<B,A>$ 는 다르다.
차수(Degree): 정점 1개에 부속된 간선 수
- 방향 그래프는 정점 차수가 진입차수(In-degree)와 진출차수(Out-degree) 로 구분된다.
- 진입차수: 정점에 들어오는 부속 간선 수
- 진출차수: 정점에서 나가는 부속 간선 수

- 왼쪽 무방향 그래프 정점 A의 차수는 3이다. B 차수는 2이다.
- 오른쪽 방향 그래프 정점 A의 진입차수는 2다. 진출차수는 1이다.
(정점이) 인접
무방향 그래프에서 두 정점 사이 간선이 있으면 두 정점이 서로 ‘인접하다’ 고 한다
(간선이) 부속
무방향 그래프에서 두 정점 사이 간선은 두 정점에 ‘부속된다’ 고 한다
그래프 경로(Path)
경로(Path)
정의
정점 시퀀스.
- $[A,B,C,D]$ : 정점 A부터 D까지 경로
- 경로 길이: 경로에 포함되는 간선 수. (시퀀스 원소 수 - 1)
단순경로(Simple Path)
정의
시퀀스 내 원소가 모두 다른 경로
싸이클(Cycle)
정의
단순경로인데, 시작 정점과 끝 정점 같다.
예시
$[A,B,C,D,A]$
- 시작 정점과 끝 정점이 같은, 단순경로다. 곧, 싸이클(Cycle)이다.
- 경로 상 정점 수: 3 (B,C,D)
- 경로 길이: 4
이 외 그래프 각종 용어
연결성분
그래프에서 정점이 서로 연결된 부분을 ‘연결성분’ 이라 한다.

A,B 두 정점이 연결되어 있다
A,B 두 정점 사이 경로(정점 시퀀스)가 있으면 두 정점은 ‘연결되어 있다’
만약 A,B 두 정점 사이 간선 방향이 있어서 두 정점 왕복할 수 있는 ‘경로’가 있다면 두 정점은 ‘강연결 되어 있다’
가중치 그래프(Weighted Graph)
간선마다 가중치 부여된 그래프
가중치는 두 정점 사이 거리, 간선 지나는 시간 등이 될 수 있다. 음수 가중치도 가능하다.
부분그래프(Sub Graph)
전체 그래프의 부분집합.
트리(Tree)
싸이클이 없는 그래프.
신장트리(Spanning Tree)
모든 정점이 연결되어 있는 트리
그래프 정점과 간선 표현 방법
그래프 G1

V(G1) = $[A,B,C]$
E(G1) = $[(A,C),(C,B),(A,B)]$
그래프 G2

V(G2) = $[E,F,G,H,I]$
E(G2) = $[(E,G),(G,I),(H,I),(F,H),(E,F),(E,H),(E,I),(F,G),(F,I),(H,G)]$
그래프 G3

V(G3) = $[J, L, N, M]$
E(G3) = $[<J, L>,<L,N>,<L,M>,<M,L>]$
그래프 저장 방법
인접행렬(Adjacency Matrix)
그래프 정점 수가 $N$ 이면 $N\times N$ 행렬에 그래프 저장(또는 표현)한다.
$0,1,2,3,…N-1$ 번 행이 정점 $0,1,2,3,…N-1$ 이다.
마찬가지로
$0,1,2,3,…N-1$ 번 열이 정점 $0,1,2,3,…N-1$ 이다.
두 정점 사이 간선 있으면 행렬 X의 a행 b열 원소를 1로 한다.
두 정점 사이 간선 없으면 그 원소를 0으로 한다.
- 가중치 그래프라면, 1 대신 간선 가중치 저장한다.
예시 - 1

- 완전그래프다.

예시 - 2


인접리스트(Adjacency List)
각 정점마다 1개씩 연결리스트(또는 배열) 이용해서 그 인접 정점 저장하는 방법
예시 - 1


- 배열 대신 연결리스트 쓴다면, 배열 각 원소를 연결리스트 각 노드에 저장하면 된다.
- 인접 정점 리스트 저장 우선순위: 다음 꺼(1) 갈 수 있었는 데 안 간거(2) 이전 꺼(3) 나머지(4)
예시 - 2


그래프 탐색
정점 방문. (후 출력)
종류
- 깊이우선탐색(DFS): 트리 전위순회를 그래프 탐색에 적용
- 너비우선탐색(BFS): 트리 레벨순회를 그래프 탐색에 적용
깊이우선탐색(DFS)
트리 전위순회 방식 그래프 탐색에 적용했다.
- 무조건 직진한다.
- 더 직진 할 데가 없을때만 후진해서 ‘갈 수 있었지만 가지 않은 곳’ 방문
- 한번 방문한 곳은 다시 방문하지 않는다.
예시 및 구현

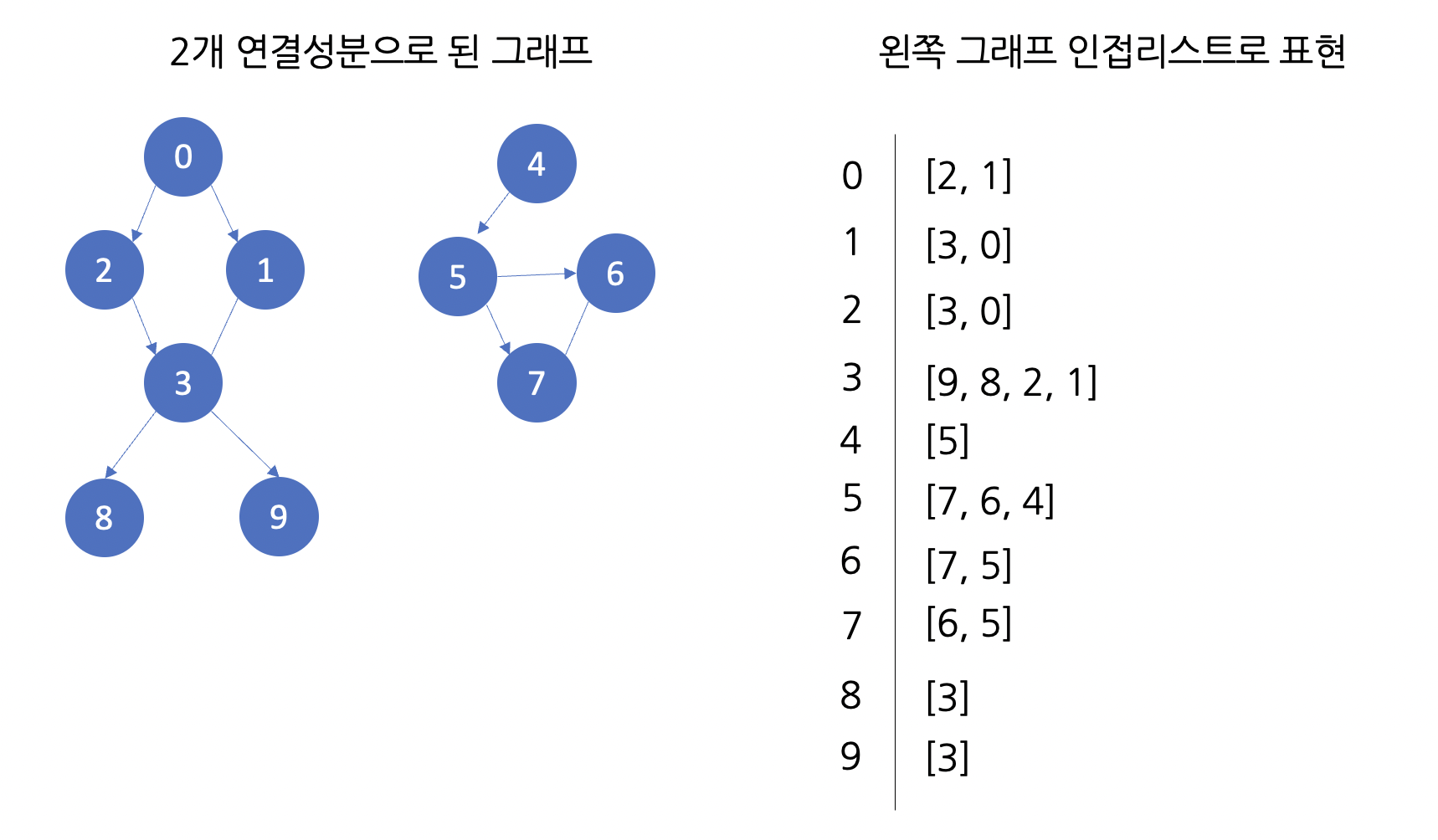
- 그래프가 2개 연결성분으로 되어 있다.
- 각 정점 방문 후 출력한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 깊이우선탐색 정의
def dfs(v) :
global adj
global visited
# 방문완료
visited[v] = True
# 출력
print(f'{v}', end=' ')
# 인접 정점으로
for w in adj[v] :
if not visited[w] : # 아직 방문 안 했다면
dfs(w) # 그 인접 정점에서 재귀호출
# 인접리스트로 표현한 그래프
adj = [
[2,1],
[3,0],
[3,0],
[9,8,2,1],
[5],
[7,6,4],
[7,5],
[6,5],
[3],
[3]
]
# 그래프 정점 수
N = len(adj)
# 정점 별 방문여부
visited = [False for x in range(N)]
# 깊이우선탐색 실행 및 결과 출력
print(f'DFS 결과:', ' ',end='')
for i in range(N) :
if not visited[i] :
dfs(i)
DFS 결과: 0 2 3 9 8 1 4 5 7 6
깊이우선 신장트리
깊이우선탐색으로 만들어지는 트리를 ‘깊이우선 신장트리’라고 한다.

- 선이 있어서 가긴 갔는데 이미 방문한 정점인 경우, 두 정점 사이 깊이우선 신장트리에서 점선으로 표시한다.
깊이우선탐색 성능
$O(N+M)$
- N은 정점 수
- M은 간선 수
N개 정점을 1번씩 만 방문한다.
M개 간선을 1번씩 만 이용한다.
미로 길 찾기 - 깊이우선탐색 메커니즘 이용
- 미로 탐색 중 ‘갈 수 있는 곳’은 모두 스택에 저장한다.
- 현재 위치 기준, 하 - 상 - 우 - 좌 순으로 다음 위치 먼저 간다.
계속 가다가 막히면 ‘이전에 갈 수 있었지만 가지 않은 곳’으로 간다.
길 찾을 미로 1
1
2
3
4
5
6
7
8
9
# 미로
map = [
[1,1,1,1,1,1],
['e',0,0,0,0,1],
[1,0,1,0,1,1],
[1,1,1,0,1,1],
[1,1,1,'x',1,1]
]
- 1은 갈 수 없는 곳이다(벽)
- e가 입구
- x가 출구
- 0이 길이다.
길 찾기 정의
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 미로 길 찾기 정의
# 미로 시작점
start = (1,0)
# 미로 크기
maze_size = (5,6)
# 현재 위치에서 갈 수 있는 곳 좌표 담을 스택
stack = []
# 갈 수 있는 길인기, 갈 수 없는 길인지 검사 정의
def isValidPos(x,y) :
if x < 0 or y < 0 or x >= maze_size[0] or y >= maze_size[1] :
return False # 갈 수 없는 길이다.
return map[x][y] == 0 or map[x][y] == 'x' # 1은 갈 수 없는 길이다.
# DFS 정의
def DFS(start) :
global stack ; global map
stack.append(start) # 미로 시작 위치
while len(stack) != 0 : # 스택이 빌 때 까지 = 갈 수 있는 곳이 없을 떼 까지
here = stack.pop() # 현재위치
print(f'{here}->', end=' ') # 현재 진행상황
(x,y) = here
if (map[x][y] == 'x') : # 현재 위치가 출구면
return True # 탈출 성공
else : # 탈출구 아니면 다음 갈 수 있는 위치 찾는다.
map[x][y] = '.' # 한번. 이미. 방문한 곳 표시 (다시 가지 않기 위함)
# 갈 수 있는 다음 위치 검사
if isValidPos(x, y-1) : stack.append((x, y-1)) # 좌
if isValidPos(x, y+1) : stack.append((x, y+1)) # 우
if isValidPos(x-1, y) : stack.append((x-1, y)) # 상
if isValidPos(x+1, y) : stack.append((x+1, y)) # 하
print(f'stack: {stack}') # 갈 수 있는 선택지들
return False # 사방이 막장이면 탈출 실패
길 찾기 실행
1
DFS(start)
(1, 0)-> stack: [(1, 1)]
(1, 1)-> stack: [(1, 2), (2, 1)]
(2, 1)-> stack: [(1, 2)]
(1, 2)-> stack: [(1, 3)]
(1, 3)-> stack: [(1, 4), (2, 3)]
(2, 3)-> stack: [(1, 4), (3, 3)]
(3, 3)-> stack: [(1, 4), (4, 3)]
(4, 3)->
True
길 찾을 미로 2
만약 미로에 출구가 없다면?
1
2
3
4
5
6
7
8
9
# 미로
map = [
[1,1,1,1,1,1],
['e',0,0,0,0,1],
[1,0,1,0,1,1],
[1,1,1,0,1,1],
[1,1,1,1,1,1]
]
길 찾기 실행
1
DFS(start)
(1, 0)-> stack: [(1, 4), (1, 1)]
(1, 1)-> stack: [(1, 4), (1, 2), (2, 1)]
(2, 1)-> stack: [(1, 4), (1, 2)]
(1, 2)-> stack: [(1, 4), (1, 3)]
(1, 3)-> stack: [(1, 4), (1, 4), (2, 3)]
(2, 3)-> stack: [(1, 4), (1, 4), (3, 3)]
(3, 3)-> stack: [(1, 4), (1, 4)]
(1, 4)-> stack: [(1, 4)]
(1, 4)-> stack: []
False
길 찾기 실패했다.
길 찾을 미로 3
1
2
3
4
5
6
7
8
9
# 미로
map = [
[1,1,1,1,'x',1],
[1,0,0,0,0,1],
[1,0,1,0,1,1],
[1,0,0,0,1,1],
[1,1,1,'e',1,1]
]
길 찾기 실행
1
2
start = (4, 3)
DFS(start)
(4, 3)-> stack: [(3, 3)]
(3, 3)-> stack: [(3, 2), (2, 3)]
(2, 3)-> stack: [(3, 2), (1, 3)]
(1, 3)-> stack: [(3, 2), (1, 2), (1, 4)]
(1, 4)-> stack: [(3, 2), (1, 2), (0, 4)]
(0, 4)->
True
너비우선탐색(BFS)
트리 레벨순회 메커니즘을 그래프 탐색에 적용했다.
- 계속 직진하면서 정점들 방문하는데, 인접 정점 있으면 거기 먼저 간다.(모양새가 레벨순회랑 비슷)
- 방문한 곳은 다시 안 들린다. 후진은 더 이상 갈 데 없을 때만 한다.
구현에 FIFO 보장되는 큐 활용한다.
예시 및 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 너비우선탐색 정의
# 큐에 삽입하는 건 그저 방문 순서대로 출력하기 위함이다.
def BFS(i) : # 점점 i
global visited ; global adj
que = [] # 큐 정의
visited[i] = True # 정점 i 방문완료
que.append(i)
while len(que) != 0 : # 방문한 곳이 없으면 멈춘다
v = que.pop(0)
print(v, end=' ')
for w in adj[v] :
if not visited[w] :
visited[w] = True # 정점 w 방문완료
que.append(w)
실행
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 주어진 그래프에서 너비우선탐색 실행
adj = [
[2,1],
[3,0],
[3,0],
[9,8,2,1],
[5],
[7,6,4],
[7,5],
[6,5],
[3],
[3]
]
N = len(adj)
visited = [False for x in range(N)]
# BFS 테스트
for i in range(N) :
if not visited[i] :
BFS(i)
0 2 1 3 9 8 4 5 7 6
너비우선 신장트리
그래프 너비우선탐색으로 만들어지는 트리를 ‘너비우선 신장트리’ 라고 한다.
위 너비우선탐색 결과로 나오는 너비우선 신장트리는 아래와 같이 표현할 수 있다.

너비우선탐색 성능
$O(N+M)$ 소요
모든 정점을 단 한번씩만 방문. 모든 간선 단 한번씩만 사용.
- N은 정점 수
- M은 간선 수
- 깊이우선탐색(DFS) 과 정점 방문 순서 & 간선 사용 순서만 다를 뿐이다.
