[Keras/딥러닝 공부] 신경망 기본 구성, 이진분류, 다중분류, 회귀문제

아래 내용은 ‘케라스 창시자에게 배우는 딥러닝 (프랑소와 슐레 저, 박해선 옮김, 길벗 출판사)’ 을 공부한 뒤, 배운 내용을 제 언어로 정리.기록한 것 입니다.

---

신경망 구조

신경망 구성.훈련에 관련된 요소들

• 층: 모델 기본 구성 단위.
• 입력값과 정답값(타겟.레이블)
• 최적화 대상인. 손실함수
• 최적화 방식. 옵티마이저

---

층(Layer)

함수. 필터

• 가중치를 갖는다. 가중치는 학습 결과이자 저장된 정보.

입력 데이터에 따른 층 구분

층 종류 별로 다른 입력 받는다.

• Dense 층(밀집 층): 벡터, 행렬(2차원 텐서)
• 순환 층: 3차원 텐서
• 2차원 합성곱 층: 4차원 텐서(이미지)

층 호환성

층들 출력과 입력 사이 연결성.

1층에서 1000 차원 벡터를 입력받아 32차원 벡터 출력했다고 가정하자.

그러면 2층은 32차원 벡터를 입력으로 받을 수 있어야 ‘층 호환성’이 보장된다.

• 케라스에서는 자동으로 층 호환성 보장해준다.

예시

from keras import models 
from keras import layers 

model = models.Sequential() 
model.add(layers.Dense(32, input_shape=(784,)))
model.add(layers.Dense(10))

1층이 784 차원 벡터를 입력받아 32차원 벡터를 출력한다.

그러면 2층은 32차원 벡터 입력받을 수 있어야 ‘층 호환성’ 이 보장된 것이다.

케라스에서는 이걸 자동 조정 해주기 때문에, 위 예시에서는 2층에 input_shape를 따로 지정하지 않았다.

---

손실함수, 옵티마이저

손실함수(목적함수)

최적화 대상.

손실함수 최솟점 잘 찾을 수록, 모형 성능은 올라간다.

• 이진분류: 이진 크로스엔트로피 (로그손실)
• 다중분류: 카테고리 크로스엔트로피 (로그손실)
• 기댓값 예측(회귀): 평균제곱오차(MSE)

옵티마이저

최적화 방법(알고리듬)

손실함수 위 특정 점에서 다른 점으로 어떻게 이동할 지 결정한다.

---

영화 리뷰 이진분류 예제

데이터셋

• 총 데이터 수: 5만
• 훈련 데이터 수: 2만 5천 개
• 검증 데이터 수: 2만 5천 개
• 훈련,검증 모두에서 긍정 리뷰, 부정리뷰 50:50 비율로 구성됨
• 이미 전처리 되어있음. 각 리뷰는 숫자(사전 값) 리스트 상태로 변환되어 있다.

데이터셋 로드

from keras.datasets import imdb
(train_data, train_labels),(test_data, test_labels) = imdb.load_data(num_words=10000)

• num_words=10000 은 훈련데이터에서 가장 자주 나타나는 1만개 단어만 쓰겠다는 뜻이다.

숮자 리스트로 된 1개 리뷰는 원래 아래와 같은 데이터였다.

word_index = imdb.get_word_index() # 사전 
reversed_word_index = dict([(value, key) for (key, value) in word_index.items()])
decoded_review = [reversed_word_index.get(i-3, '?') for i in train_data[0]]

for i in decoded_review : 
    print(i, end=' ')
print()

• ? 는 사전에 없는 단어라서 ?가 된거다.

---

데이터 전처리

신경망에 데이터 넣으려면 데이터를 원핫 인코딩 벡터 꼴로 바꿔야 한다.

그리고 변환된 원핫 인코딩 벡터를 Dense 층에 넣는다.

입력 데이터(벡터) 모두 원핫 인코딩 벡터 꼴로 변환

# 입력데이터의 원핫인코딩 행렬 구한다. 
import numpy as np

def vectorize_sequence(sequence, dimension=10000) : 
    zero_matrix = np.zeros((len(sequence), dimension)) # (25000, 10000) 영행렬 
    for i, sq in enumerate(sequence) : 
        zero_matrix[i, sq] = 1. # 영벡터에서 sq 위치 전부 1로 바꾼다. -> 원핫 인코딩 벡터 25000개로 구성된 행렬이 된다. 
    return zero_matrix 
x_train = vectorize_sequence(train_data); x_test = vectorize_sequence(test_data) # 변환된 원핫 인코딩 '행렬' 2개. 

• (리뷰 수, 10000) 크기 영행렬 만든다. 이 행렬은 이제 행은 각 리뷰, 열은 사전 인덱스 0~10000의 각 단어가 문장(리뷰)에 있고 없고를 나타낼 것이다.
• 각 리뷰에서, 문장 안에 단어(열)가 있으면 1, 아니면 0을 코딩한다.
• 최종 결과는 ‘원핫 인코딩 행렬’ 이 나온다.

위 방법으로 훈련용, 검증용 입력 데이터 모두 원핫 인코딩 벡터로 바꾼다.

정답값(타겟값) 모두 원핫 인코딩 벡터 꼴로 변환

타겟값은 숫자 리스트지만, 그 내용물은 모두 1 또는 0이다. 따라서 넘파이 배열로만 변환해주면 된다.

y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32') # 정답값도 전부 ndarray 꼴로 변환한다. 

데이터를 ‘모델에 넣기 적합한 상태’로 만들었다.

이제 모델을 정의하자.

---

신경망 모델 정의

# GPU 확인
import tensorflow as tf
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))

Num GPUs Available: 1

# 모델 정의 
from keras import models 
from keras import layers

model = models.Sequential()
# 1층 
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
# 2층 
model.add(layers.Dense(16, activation='relu'))
# 3층 (출력 층)
model.add(layers.Dense(1, activation='sigmoid'))

1층의 매개변숫값 16은 은닉유닛 갯수를 말한다.

1층에 (10000,1) 크기 벡터를 입력데이터로 넣으면, 가중치 $w$와 벡터를 내적하면서 입력 데이터가 16차원 공간으로 투영된다.

곧, 벡터의 차원축소가 일어난다. 벡터를 차원축소 함으로써 원본 벡터에서 노이즈를 모두 날리고, 핵심 특징 부분만 남게 된다(16차원 공간의 기저벡터 선형조합).

차원축소된 벡터에 편향벡터를 더하고, relu 함수를 요소별로 적용한다.

• 은닉유닛 늘리면 벡터가 더 고차원 공간에 투영되면서, 신경망이 더 복잡한 표현을 학습하게 된다.
• 다만 계산시간 늘어나게 된다. 또 내가 학습시키고자 하는 패턴 이외 다른 패턴 학습할 수도 있다.
• 다른 패턴까지 학습하게 되면 훈련데이터는 정말 잘 맞추게 되지만, 검증 데이터에서는 오히려 성능 떨어질 수 있다.

모델 컴파일

# 모델 컴파일 
model.compile(
    optimizer='rmsprop',
    loss = 'binary_crossentropy',
    metrics=['accuracy']
)

• 최적화 방법(옵티마이저)은 확률적 경사하강법 알고리듬을 선택했다.
• 예측 손실(오차)은 이진 크로스엔트로피 사용해 계산할 것이다.
• 모델 성능은 정확하게 분류한 비율 사용해 측정하겠다.

크로스엔트로피

쿨백-라이블러 발산값은 두 분포 모양 서로 다른 정도 나타낸다.

쿨백 라이블러 발산과 크로스엔트로피 사이 관계는 아래 식으로 나타낼 수 있다.

$KL(p\vert\vert{q}) = H[p,q] - H[p]$

위 이진분류 문제에서 정답 분포는 0 또는 1 하나 값 확률이 1인 베르누이 분포다.

곧, 정답값의 분포는 엔트로피가 0이다.

$H[p] = 0$

따라서 위 식은 아래와 같아진다.

$KL(p\vert\vert{q}) = H[p,q]$

예측분포와 정답분포의 쿨백-라이블러 발산 값(두 분포 모양 다른 정도) 는 두 분포 크로스엔트로피 값과 같다.

곧, 이 문제에서 두 분포의 크로스엔트로피는 두 분포 모양 다른 정도를 나타낸다.

두 분포 모양 다른 정도는 곧 모델의 예측 손실을 의미한다.

모형에 입력 데이터를 배치 사이즈에 맞춰 넣으면(예:128개 1묶음), 각 개별 데이터 별 크로스엔트로피 값(손실값)이 나올 것이다.

이 손실값들 평균 낸 것을 로그손실($Log loss$) 이라고 한다.

이 로그손실은 현재 가중치에서 손실이고, 모형의 손실함수로 사용된다.

---

새 데이터셋에서 모델 성능 얼마나 나오는지 측정 위한 검증용 셋 만들기

원본 훈련데이터에서 10,000개 표본을 떼어서 검증용 셋으로 만들겠다.

# 모델 성능 검증 위한 테스트셋 만들기 
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]

모델 훈련시키기

# 모델 훈련 
hs = model.fit(
    partial_x_train, 
    partial_y_train,
    epochs = 20,
    batch_size=512,
    validation_data=(x_val, y_val)
)

검증용 셋 만들고 남은 훈련용 데이터 partial_x_train 과 partial_y_train(타겟) 이용해 모형을 학습시켰다.

데이터는 512개를 한 묶음으로 삼아 훈련시켰다. 곧, 512개를 예측하도록 하고 512개 다 하면 그때 정답 확인해서 손실 계산. 가중치 수정했다.

전체 데이터셋에 대해 에포크는 20번 반복했다.

종합하면 에포크 1회 당 전체 데이터셋 데이터를 512개씩 묶음으로 가중치를 수정한다. 이 과정을 20번 반복한다.

그리고 1회 에포크를 마치면 x_val, y_val 검증용 데이터셋을 이용해 로그손실 값과 정확하게 분류한 비율을 계산한다.

*책에서는 위 훈련과정이 20초 이상 걸릴 것이라 했지만, GPU를 사용해서 그런지 전 과정에 10초도 걸리지 않았다.

훈련 마친 후 - 에포크 별 손실, 정확도 출력

model.fit() 객체의 history 속성은 훈련하면서 발생한 에포크 별 손실, 정확도를 딕셔너리 형태로 담고 있다.

history_dict = hs.history
history_dict.keys()

dict_keys([‘loss’, ‘accuracy’, ‘val_loss’, ‘val_accuracy’])

import pandas as pd
pd.DataFrame(history_dict)

왼쪽부터 순서대로 i번 에포크에서 훈련 손실, 훈련 정확도, 검증 손실, 검증 정확도 나타낸다.

위 데이터프레임을 그래프로 옮기면 내용을 시각적으로 한눈에 볼 수 있을 것이다.

# 훈련, 검증 손실 그래프로 그리기 
import matplotlib.pyplot as plt

loss = history_dict['loss']
val_loss = history_dict['val_loss']

epochs = range(1, len(loss)+1) # 1~20

plt.plot(epochs, loss, 'bo', label='loss while training')
plt.plot(epochs, val_loss, 'b', label='loss while validation')
plt.title('Training and Validation loss')
plt.xlabel(f'Epochs')
plt.ylabel(f'Loss')
plt.legend()
plt.show()

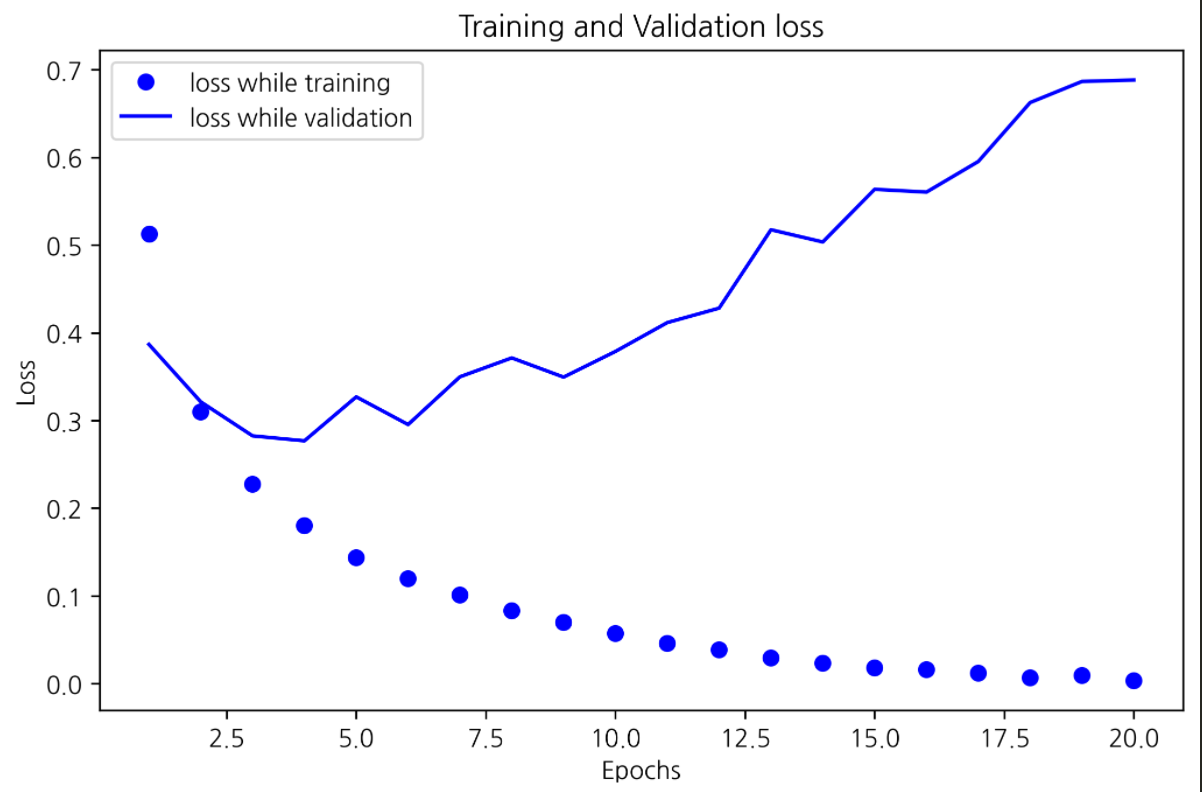
그래프 해석 및 추측

약 3번째 ~ 4번째 반복부터 과적합이 발생 한 것 같다. 그래프를 보면 훈련용 셋에서 손실은 계속 줄어들어 0에 수렴하지만, 검증용 셋에서 약 4번째 에포크 후 부터는 점차 손실이 증가하는 걸 관찰할 수 있다.

훈련용 셋에 오버피팅 발생했기 때문에, 새 데이터를 모델에 넣으면 제대로 성능이 안 나올 것이다.

한편 아래는 훈련용, 검증용 셋에서 정확도 그래프다.

# 훈련, 검증 정확도 그래프로 그리기 
plt.clf() # 그래프 초기화 
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']

plt.plot(epochs, acc, 'ro', label='Training accuracy')
plt.plot(epochs, val_acc, 'r', label='Validation accuracy')
plt.title(f'Training and Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

정확도 그래프에서도 과적합 발생이 짐작되는 형태가 나왔다.

약 4번째 에포크 넘어가면 과적합 발생했다. 그러면 모델을 새로 정의하고, 4번만 반복해서 과적합을 완화시켜 보자.

# 20번 반복하면서 과적합 발생했다. 
# 4번만 반복해서 과적합을 완화해보자. 
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

# 모델 컴파일 
model.compile(
    optimizer='rmsprop',
    loss='binary_crossentropy',
    metrics=['accuracy']
)

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test)

result

[0.2950170338153839, 0.8840000629425049]

에포크 4번만 반복했을 때는 약 88% 정확도가 나왔다.

이번에도 에포크 별 손실과 정확도를 그래프로 나타내면 아래와 같았다.

train_loss = hd.history['loss']
test_loss = hd.history['val_loss']

train_acc = hd.history['accuracy']
test_acc = hd.history['val_accuracy']

epochs = range(1, len(hd.history['accuracy'])+1)

plt.subplot(1,2,1)
plt.plot(epochs, train_loss, 'bo', label='Training loss')
plt.plot(epochs, test_loss, 'b', label='Test loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title(f'Training loss and Test loss')
plt.legend()

plt.subplot(1,2,2)
plt.plot(epochs, train_acc, 'ro', label='Training Accuracy')
plt.plot(epochs, test_acc, 'r', label='Test Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title(f'Training and Test Accuracy')
plt.legend()
plt.tight_layout()
plt.show()

모델에 새 데이터 넣어서 예측하기

위에서 훈련시킨 모델에 새 데이터를 넣어서 분류해보자.

• predict() 메소드를 사용하면 모델에 예측 명령 내릴 수 있다.

# 훈련된 모델이(가중치가) 새 데이터를 어떻게 분류하는 지 관찰하자. 
r = model.predict(x_test)

# 예측 결과 
r

출력 벡터의 각 스칼라 값들은 해당 데이터(리뷰)가 긍정리뷰(1)일 확률이다.

추가실험

은닉 유닛을 늘렸을 때 검증 정확도 변화는?

• 은닉 유닛 기존 16개에서 32개로 늘렸을 때 정확도 변화

# 은닉 유닛을 더 늘렸을 때 
model3 = models.Sequential()
model3.add(layers.Dense(32, activation='relu', input_shape=(10000,)))
model3.add(layers.Dense(32, activation='relu'))
model3.add(layers.Dense(1, activation='sigmoid'))

model3.compile(
    optimizer='rmsprop',
    loss='binary_crossentropy',
    metrics=['accuracy']
)

result = model3.fit(partial_x_train, partial_y_train, batch_size=512, epochs=20, validation_data= (x_val, y_val))

plt.figure(figsize=(10,5))
plt.plot(range(1, 21), result.history['accuracy'], 'go', label='training accuracy')
plt.plot(range(1, 21), result.history['val_accuracy'], 'g', label='validation accuracy')
plt.legend()
plt.show()

은닉 유닛 32개일 때, 16개 일 때 보다 과적합이 더 빨리 나타났다.

16개 일 때는 4번째 에포크 쯤에서 과적합 나타났다.

하지만 32개일 때는 3번째 에포크 이후부터 과적합 관찰됬다.

또 16개 은닉유닛일 때는 에포크 반복 초반에는 일단 검증 셋 정확도가 조금씩 증가하는 양상이었다면, 32개 일 때 는 정확도가 일단 감소하면서 시작됬다.

• 은닉 유닛 64개로 늘렸을 때 모델 검증 정확도 변화

# 은닉 유닛 64개이면? 
model4 = models.Sequential() 
model4.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model4.add(layers.Dense(64, activation='relu'))
model4.add(layers.Dense(1, activation='sigmoid'))

model4.compile(
    optimizer='rmsprop',
    loss='binary_crossentropy',
    metrics=['accuracy']
)

result = model4.fit(partial_x_train, partial_y_train, batch_size=512, epochs=20, validation_data=(x_val, y_val))

plt.plot(range(1, 21), result.history['accuracy'], 'bo', label='training accuracy')
plt.plot(range(1, 21), result.history['val_accuracy'], 'b', label='Validation accuracy')
plt.legend()
plt.show()

은닉유닛 64개일 때는 약 2번째 에포크 쯤 부터 검증 정확도가 떨어지기 시작했다.

반면 훈련용 데이터셋에서 정확도는 같은 구간에서 계속 증가한다.

$\Rightarrow$ 은닉유닛을 너무 많이 추가하면 과적합이 더 빨리 나타났다.

---

뉴스 기사 다중 분류 문제

다중 분류 문제 정의: 데이터가 2개 이상 클래스(여러 카테고리값)로 분류되는 문제

로이터 데이터셋

from keras.datasets import reuters

(train_data, train_label), (test_data, test_label) = reuters.load_data(num_words=10000)

• 46개 토픽(46개 레이블), 각 레이블값은 0과 45 사이 정수다.
• 8,982개 훈련용 데이터, 2,246개 검증용 데이터
• 각 표본은 숫자로 된 리스트다. 위 이진분류 문제 때와 같다.

예) 0번째 데이터는 원래 아래와 같았다.

# 0번째 데이터 디코딩

word_index = reuters.get_word_index()
reversed_word_index = dict([(value, key) for (key, value) in word_index.items()])
decoded_news = ' '.join([reversed_word_index.get(i-3, '?') for i in train_data[0]])
decoded_news

’? ? ? said as a result of its december acquisition of space co it expects earnings per share in 1987 of 1 15 to 1 30 dlrs per share up from 70 cts in 1986 the company said pretax net should rise to nine to 10 mln dlrs from six mln dlrs in 1986 and rental operation revenues to 19 to 22 mln dlrs from 12 5 mln dlrs it said cash flow per share this year should be 2 50 to three dlrs reuter 3’

• 사전을 만들고, 1개 샘플에서 각 단어를 사전 숫자값으로 바꾼 뒤 그걸 리스트에 담은 거다.

---

데이터셋을 원핫 인코딩 벡터로 변환

입력데이터 원핫 인코딩 벡터로 변환

원핫 인코딩 벡터 꼴로 변화된 각 데이터를 벡터, 행렬 입력 받는 신경망 Dense층에 넣을 것이다.

벡터 변환 방법은 위 이진분류 문제와 같다.

# 데이터 전처리 - 각 데이터(문장) 원핫 인코딩 벡터 꼴로 변환 
import numpy as np 
def vectorize_sequence(sequence, dimension=10000) : 
    matrix = np.zeros((len(sequence), dimension))
    for i, sq in enumerate(sequence) :
        matrix[i, sq] = 1.
    return matrix
x_train = vectorize_sequence(train_data)
x_test = vectorize_sequence(test_data)

레이블 값 원핫 인코딩 벡터로 변환

여기서는 이진분류 문제와 달리 레이블 값이 0과 45 사이 정수다.

레이블 값들도 모두 원핫 인코딩 벡터로 바꿔준다.

$\Rightarrow$ 원핫 인코딩 벡터를 행으로 쌓은 행렬이 나올 것이다.

# 레이블 원핫 인코딩 벡터로 변환 
def invert_one_hot(sequence, dimension=46) : 
    matrix = np.zeros((len(sequence), dimension))
    for i, sq in enumerate(sequence) : 
        matrix[i, sq] = 1.
    return matrix 
one_hot_train_label = invert_one_hot(train_label)
one_hot_test_label = invert_one_hot(test_label)

---

모델 정의

층을 순서대로 쌓아올린 Sequential() 모델을 정의하겠다.

# 모델 정의

model = models.Sequential() 
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

• 다중분류를 하는 게 목적임으로, 맨 마지막 출력층 활성화 함수를 소프트맥스 함수로 지정한다. 소프트맥스 함수는 46차원 출력벡터 각 요소를 확률 꼴로 바꿔준다. 소프트맥스 함수 거친 모델의 최종 출력벡터는 데이터 1개가 각 0~45 범줏값일 확률 나타낸다.

모델 컴파일

# 모델 컴파일 
model.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy']
)

• 손실계산 방법에 카테고리 크로스엔트로피 사용했다. 소프트맥스 함수 거친 출력의 확률분포와 정답값의 카테고리 확률분포 모양이 서로 다른 정도 나타낸다. 이때 손실함수는 카테고리 로그 손실($Categorycal log loss$) 가 된다.

훈련용 셋에서 검증용 셋 따로 떼어내기

모델 훈련시키고, 성능 검증하기 위해 검증용 셋 1,000개를 따로 떼어냈다.

x_val = x_train[:1000]
partial_x_train = x_train[1000:]

y_val = one_hot_train_label[:1000]
partial_y_train = one_hot_train_label[1000:]

모델 훈련

에포크는 20번, 배치 사이즈는 512로 지정하고 모델을 훈련시켰다.

# 모델 훈련 
training_result = model.fit(partial_x_train, partial_y_train, batch_size=512, epochs=20, validation_data=(x_val, y_val))

#plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
epochs = range(1,21)
plt.plot(epochs, training_result.history['accuracy'], 'bo', label='Traning Accuracy')
plt.plot(epochs, training_result.history['val_accuracy'], 'b', label='Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('Training & Validation Accuracy')
plt.legend()

plt.subplot(1,2,2)
plt.plot(epochs, training_result.history['loss'], 'ro', label='Traning Loss')
plt.plot(epochs, training_result.history['val_loss'], 'r', label='Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Training & Validation Loss')
plt.legend()

plt.tight_layout()
plt.show()

20번 에포크를 돌았는데, 한 9번째 에포크 부터 과적합 나타나는 것 같다.

과적합 완화하기 위해 에포크를 9로 조정하고 다시 모델 학습시키자.

# 에포크 9번으로 조정하고 모델 새로 훈련시키기 
# 모델 정의
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

# 모델 컴파일 
model.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy']
)

# 모델 훈련 
model.fit(x_train, one_hot_train_label, epochs=9, batch_size=512)

result2 = model.evaluate(x_test, one_hot_test_label)
result2

[0.9699822664260864, 0.7947462201118469]

검증용 데이터셋에서 약 79% 정확도가 나왔다.

새로운 데이터 예측하기

학습된 모델에 새 데이터를 넣어서, 분류하도록 해보자.

predictions = model.predict(x_test)

# 0번째 데이터 예측 결과
predictions[0] # 소프트맥스함수 통과한 확률꼴 값들 

• 0번째 데이터가 0~45로 각각 분류될 확률을 나타낸다.
• 확률 꼴 값들이므로, 전체 총합도 1이다.

sum(predictions[0])

1.0000001185512701

위 벡터가 담고있는 확률값들을 시각화 해보자.

sns.barplot(np.arange(0, 46, 1), predictions[0])
plt.tight_layout()
plt.title('Topic prediction result: 3')
plt.show()

모델은 0번째 데이터를 3으로 분류했다.

실제 정답은 뭐였는지 확인해보자.

train_label[:10][0] # 실제 정답 

3

---

모델을 정의할 때, 충분히 큰 중간층 두어야 한다.

중간층 히든유닛이 출력 벡터 차원보다 작은 경우.

그 층에서 ‘정보의 병목현상’이 발생한다.

위 경우. 입력 데이터를 저차원 공간으로 투영하게 되는데, 너무 저차원 공간으로 투영해버리면서 분류에 필요한 핵심 특성들이 층을 다 통과하지 못하게 된다.

결국 중간층 히든유닛이 너무 작으면, 모델 분류성능도 떨어지게 된다.

위에서 모델 정의할 땐 중간층 히든유닛을 64개로 지정했다.

만약 히든유닛을 32개로 지정하면 어떻게 될까.

이 경우 히든유닛 갯수는 내가 분류하고자 하는 카테고리 수 46보다 작다.

아마 모델의 분류 성능이 다소 떨어지게 될 것 같다.

# 추가 실험 
# 중간 층 유닛크기를 32로 해보자. 
# 모델 정의
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

# 모델 컴파일
model.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy']
)

# 모델 학습 
result = model.fit(x_train, one_hot_train_label, batch_size=512, epochs=9, validation_data=(x_test, one_hot_test_label))

plt.figure(figsize=(10,5))
plt.plot(range(1,10), result.history['accuracy'], 'bo', label='Traning Accuracy')
plt.plot(range(1,10), result.history['val_accuracy'], 'b', label='Validation Accuracy')
plt.legend()
plt.show()

검증 데이터셋에서 최고 정확도가 78.76 정도 나왔다. 유닛크기를 64로 했을 때 검증 셋 정확도가 79.47 정도였다.

아주 큰 정도는 아니지만 모델 성능이 살짝 떨어진 것을 관찰할 수 있었다.

유닛크기를 더 줄여보자 $\Rightarrow$ 10

# 유닛 크기를 더 줄여보자. --> 10 
def training_model(unit_num):
    global x_train 
    global one_hot_train_label
    global x_test
    global one_hot_test_label

    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
    model.add(layers.Dense(int(unit_num), activation='relu'))
    model.add(layers.Dense(46, activation='softmax'))

    # 모델 컴파일
    model.compile(
        optimizer='rmsprop',
        loss='categorical_crossentropy',
        metrics=['accuracy']
    )

    # 모델 학습 
    result = model.fit(x_train, one_hot_train_label, batch_size=512, epochs=9, validation_data=(x_test, one_hot_test_label))

    plt.clf()
    plt.figure(figsize=(10,5))
    plt.plot(range(1,10), result.history['accuracy'], 'bo', label='Traning Accuracy')
    plt.plot(range(1,10), result.history['val_accuracy'], 'b', label='Validation Accuracy')
    plt.legend()
    plt.show()
training_model(10)

중간층 히든유닛 갯수를 10개로 줄이니 검증셋 정확도가 78%에서 74% 까지 4% 정도 떨어졌다.

데이터가 너무 저차원으로 차원축소 되면서 분류에 필요한 정보가 제대로 걸러지지 않았고, 결과로 제대로 분류가 안 됬다고 추측할 수 있다.

은닉유닛 수를 64보다 증가시켰을 때

def training_model(unit_num, layer_added_num):
    global x_train 
    global one_hot_train_label
    global x_test
    global one_hot_test_label

    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
    for i in range(layer_added_num) : 
        model.add(layers.Dense(int(unit_num), activation='relu'))
    model.add(layers.Dense(46, activation='softmax'))

    # 모델 컴파일
    model.compile(
        optimizer='rmsprop',
        loss='categorical_crossentropy',
        metrics=['accuracy']
    )

    # 모델 학습 
    result = model.fit(x_train, one_hot_train_label, batch_size=512, epochs=9, validation_data=(x_test, one_hot_test_label))

    plt.clf()
    plt.figure(figsize=(10,5))
    plt.plot(range(1,10), result.history['accuracy'], 'bo', label='Traning Accuracy')
    plt.plot(range(1,10), result.history['val_accuracy'], 'b', label='Validation Accuracy')
    plt.legend()
    plt.show()

# 유닛 수 = 64 일 때 
training_model(64, 1)

검증 셋 최고 정확도: 0.7988

# 유닛 수 = 128 일 때 
training_model(128,1)

검증 셋 최고 정확도: 0.8032

# 유닛 수 = 512 일 때 
training_model(512,1)

검증 셋 최고 정확도: 0.7934

처음예상: 은닉유닛 수를 46차원보다 너무 크게 올리면(128, 512) 처음 (10000,1) 벡터가 차원축소하면서 너무 많은 노이즈가 벡터에 남게 될 것이다.

노이즈가 많이 남아도 제대로 분류하기 어려울 것이다.

$\Rightarrow$ 은닉유닛 수를 너무 크게 올려도 제대로 분류가 안 될 것이다.

결과: 은닉유닛 수 128, 512 일 때 대체로 정확도가 64일때 보다 낮게 나왔지만, 항상 그렇지는 않았다.

---

회귀문제에 신경망 적용하기

신경망 써서 기댓값 예측하기.

보스턴 주택 가격 데이터셋

from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

• 총 샘플 수 506개 (훈련용:404개, 테스트용:102개)
• 입력 데이터에 있는 각 특성은 스케일(값의 범위)이 서로 다르다.
• 데이터셋이 13개 속성 갖는다.
• 타깃값: 주택의 중간 가격

데이터 준비

이 데이터셋은 각 속성값들 스케일이 모두 다르다.

이런 경우 값들 간 스케일이 비슷해지도록 맞춰줘야 한다.

정규화(표준화)

$\frac{X_{i}-mean}{s}$

각 값들을 정규화 함으로써 스케일을 맞춰줄 수 있다.

각 속성(열)의 평균과 표준편차를 구한 뒤 정규화 하면 된다.

• 주의) 테스트 셋도 훈련용 셋의 평균과 표준편차로 정규화 한다.

정규화 하면 각 속성값들은 모두 평균이 0이 되고 표준편차는 1이 된다.

$\Rightarrow$ 모든 값들이 대략 0~1 사이로 몰리게 된다.

# 훈련용 데이터 정규화 

mean = train_data.mean(axis=0) # axis=0: 행 방향 
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

# 검증용 데이터 정규화 

test_data -= mean 
test_data /=std

---

모델 정의

데이터 수가 작을 때는 은닉 층 수 작은 모델 쓰는게 과적합 방지할 수 있다.

# 모델 구성 
def build_model() : 
    # 모델 정의
    model = models.Sequential() 
    model.add(layers.Dense(64, activation='relu', input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1)) # 선형 층  # 기댓값 에측치만 모든 범위에서 내놓을 것이다. 

    # 모델 컴파일
    model.compile(
        optimizer='rmsprop',
        loss = 'mse',
        metrics=['mae']
    )
    return model 

• 이 모델 마지막 층은 활성화 함수가 없다. 이런 층을 선형 층 이라고 한다. 함수에 비유하면 $y = W\cdot{X} + b$ 이런 꼴 일거다. $W$ 는 가중치 행렬, $b$ 는 편향 벡터다. 앞에서 처럼 활성화 함수로 시그모이드 함수를 적용하면 위 함수 결과값을 0과 1 사이에서 나오도록 제한한다. 반면 여기서는 활성화 함수가 없으므로, 위 선형함수 형상처럼 출력값 $y$ 가 전 구간에서 나올 수 있게 된다.

• 회귀문제의 손실함수로 평균 제곱 오차($mse$) 를 적용했다. 이 값은 예측값(기댓값 예측치)과 타깃(기댓값) 사이 잔차의 제곱을 평균낸 것이다.
• 모형의 성능 측정 지표로 평균 절대 오차($mae$) 를 적용했다. 이 값은 예측값과 타깃값 사이 잔차 절댓값을 평균 낸 것이다.

---

K-fold 교차검증으로 모델 성능 측정

데이터 수 적을 때 유용한 방법

보스턴 집값 데이터셋은 표본 수가 적다. 이렇게 데이터 수가 적을 때는 K-fold 교차검증을 사용하면 모델 성능을 신뢰성 있게 측정할 수 있다.

방법

K-fold 교차검증은 전체 데이터셋을 K 개로 분할하고. 그 중 1개를 검증용 셋, 나머지 K-1개를 훈련용 셋으로 써서 모델 훈련. 검증한다. 이 과정을 검증용 셋을 바꿔가며 K번 반복한다.

결과로 K개 검증점수(MAE 값)가 나온다. 이 K개 검증점수 평균내서 모델의 최종 검증점수로 삼는 방법이다.

에포크 = 100일 때 수행

에포크를 100번으로 설정했다. Fold 수는 4이다.

아래 코드의 흐름은 다음과 같다.

• 검증용 셋 / 훈련용 셋 분할
• 훈련용 셋으로 모델 학습
• 검증용 셋에서 모델 성능 평가

# k겹 교차검증 
import numpy as np 

k = 4
num_val_samples = len(train_data)//k
num_epochs = 100 
all_scores = [] 

for i in range(k) : 
    print(f'처리 중인 폴드: {i}')
    val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
    val_targets = train_targets[i*num_val_samples:(i+1)*num_val_samples]

    partial_train_data = np.concatenate([
        train_data[:i*num_val_samples],
        train_data[(i+1)*num_val_samples:]
    ], axis=0)
    partial_train_targets = np.concatenate([
        train_targets[:i*num_val_samples],
        train_targets[(i+1)*num_val_samples:]
    ], axis=0)

    model = build_model() 
    model.fit(partial_train_data, partial_train_targets, epochs=num_epochs, batch_size=1, verbose='0')
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose='0')
    all_scores.append(val_mae)

Fold 가 4개 이므로 4개의 모델 성능 평가 점수가 나온다.

Fold 별 검증 점수의 평균을 내서 모델의 최종 검증 점수 구한다.

np.mean(all_scores) # 최종 검증점수 

2.3305585384368896

최종 MAE 값이 2.33 나왔다.

모델의 기댓값 예측이 빗나가는 정도(크기)가 예측값에서 $\pm{2300}$ 달러 정도 날 수 있다는 뜻이다.

에포크 = 500 일 때 수행

에포크를 100에서 500으로 늘리고 같은 방법으로 모델 다시 학습시켰다.

num_epochs = 500 
all_mae_histories = []
num_val_samples = len(train_data) // k

for i in range(k) : 
    print(f'처리 중인 폴드:{i}')
    # 데이터 
    val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
    val_label = train_targets[i*num_val_samples:(i+1)*num_val_samples]

    partial_train_data = np.concatenate([
        train_data[:i*num_val_samples],
        train_data[(i+1)*num_val_samples:]
    ], axis=0)
    partial_train_label = np.concatenate([
        train_targets[:i*num_val_samples],
        train_targets[(i+1)*num_val_samples:]
    ], axis=0)
    # 모델
    model = build_model() 
    history = model.fit(partial_train_data, partial_train_label, epochs=num_epochs, batch_size=1, validation_data=(val_data, val_label), verbose='0')
    all_mae_histories.append(history.history['val_mae'])

k_fold_score_per_epoch = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

# mae plot
plt.plot(range(1, num_epochs+1), k_fold_score_per_epoch)
plt.xlabel('The number of Epochs')
plt.ylabel('Validation MAEs')
plt.title('Validation MAE per Epoch')
plt.show()

흐름

• 훈련용 셋 / 검증용 셋으로 나눈다.
• 훈련용 셋으로 모델 학습시킨다. batch_size=1 이고 에포크가 500 이므로, 에포크 1번 당 훈련용 데이터 갯수만큼 가중치를 조정할 것이다. 이 과정을 총 500번 반복한다.
• 에포크 1번이 끝나면 학습된 모델에 검증용 셋 적용한다. 여기서 MAE 구한다. 에포크가 총 500번이므로, MAE 값도 에포크 당 1개씩 해서 총 500개 나온다.
• K번 검증용 셋을 바꿔가며 위 과정을 실시하면, MAE 값 500개가 들은 리스트가 총 K개 나온다. 이 경우 4개다. 결과로 all_mae_histories는 크기가 (4, 500) 이다.
• 마지막으로 에포크 당 모델 성능점수를 구한다. 곧, 에포크 별로 K개 분할에서 MAE 점수 평균을 구한다. 총 500개가 나온다.

에포크 별 모델 성능 최종점수를 그래프로 나타내면 아래와 같다.

그래프에서 좀 더 쓸만한 정보를 얻고자 데이터를 아래와 같이 변형하자.

• 에포크 횟수가 늘 수록 모델이 훈련되면서 검증용 셋에서도 잔차 크기가 줄어들 것이다. 위 그래프의 0 근처 초반 구간에서 나타나는 현상(MAE가 급격히 감소)은 대체로 예상가능하고 당연한 결과다. 이 부분을 없애자.
• 또한 이 부분은 그래프 나머지 부분과 스케일이 너무 많이 차이난다. 제외한다.
• 각 값들을 이전 포인트의 지수 이동 평균으로 대체함으로써, 값들 크기를 조정한다.

# mae 값들 지수이동평균으로 크기 변환 
# 지수이동평균으로 변환 과정 정의

def smooth_curve(points, factor=0.9) : 
    smooth_points = [] 
    for i in points : 
        if smooth_points : 
            previous = smooth_points[-1]
            smooth_points.append(previous*factor + i*(1-factor))
        else : 
            smooth_points.append(i)
    return smooth_points 

smooth_mae_history = smooth_curve(k_fold_score_per_epoch[10:]) # mae 값 모두 크기 변환

plt.figure(figsize=(10,5))
plt.plot(range(10, num_epochs), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.title('Validation MAE per Epochs')
plt.plot(80, 2.35, 'ro')
plt.show()

변환된 값들의 그래프에서 빨간 점에 주목하자.

약 80번째 에포크를 기점으로 감소하던 MAE 값이 다시 증가한다.

80번째 에포크 이후부터 모델에 과적합이 발생했다고 추측할 수 있다.

$\Rightarrow$ 새 데이터에서 모델 예측 성능을 끌어올리기 위해 에포크 횟수를 80으로 조정한다.

에포크 횟수에 대한 최적 매개변수를 찾았다. 이제 최적 파라미터와 전체 훈련용 데이터를 사용해서 모델 훈련하고, 검증용 셋으로 모델 성능 검증해보자.

model = build_model() 
model.fit(train_data, train_targets, epochs=80, batch_size=16, verbose='0')

test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
test_mae_score # MAE 약 2.55 기록했다. 

2.550393581390381

• 최적 에포크 횟수 적용했음에도 MAE 값이 크게 줄진 않았다.