선형계획법 문제 (LP 문제)
$Linear$ $Programming$
정의 :
선형모형 $c^{T}x$ 을 등식/부등식 제한조건 걸고 최적화 하는 문제
목적함수
- $c^{T}x$
연립방정식 제한조건 (등식 제한조건)
- ‘기본형’ 선형계획법 문제
$Ax = b$
- $x \ge 0$ (벡터 $x$ 의 모든 원소는 0 또는 양수)
연립부등식 제한조건 (부등식 제한조건)
‘정규형’ 선형계획법 문제
$Ax \leq b$
$x \ge 0$ (벡터 $x$ 의 모든 원소는 0 또는 양수)
제한조건을 $Ax = b$, $Ax \leq b$ 로 표시한 것은 사이파이 패키지에 넣을 때 $A$, $b$ 등을 따로따로 명시해서 넣어야 하기 때문이다.
제한조건 표기방식만 다를 뿐, 일반적인 제한조건 최적화 문제와 똑같다.
$\Rightarrow$ 그냥 똑같은 제한조건 최적화 문제인데, 목적함수가 선형모형인 경우라 생각하면 된다.
사이파이로 LP 문제 해결하기
sp.optimize.linprog(f, A_ub, b_ub, A_eq, b_eq, )
- f : 목적함수. 선형모형
- A_ub : 연립부등식 제한조건의 행렬 $A$
- b_ub : 연립부등식 제한조건의 벡터 $b$
- A_eq : 연립방정식 제한조건의 행렬 $A$
- b_eq : 연립방정식 제한조건의 벡터 $b$
1
2
# 사이파이 선형계획법 명령
sp.optimize.linprog(f, A_ub, b_ub...)
사용 예)
목적함수 : $-3x-5y$
연립부등식 제한조건 :
- $-x \leq -100$
- $-y \leq -100$
- $x+2y \leq 500$
- $4x+5y \leq 9800$
$x \ge 0, y \ge 0$
위 경우에서,
$c = [-3, -5]^{T}$
$A = [[-1,0],[0,-1],[1,2],[4,5]]$
$b = [-100, -100, 500, 9800]^{T}$
이다.
이걸 sp.optimize.linprog() 명령에 argument 로 넣으면 된다.
알고리듬 안에 $x \ge 0, y \ge 0$ 은 기본 적용되어 있다.
1
2
3
4
5
6
c = np.array([-3, -5])
A = np.array([[-1,0],[0,-1],[1,2],[4,5]])
b = np.array([-100,-100, 500, 9800])
# 선형계획법 명령
sp.optimize.linprog(c, A, b)
CVXPY 이용해서 선형계획법 문제 풀기
CVXPY 를 이용해서 선형계획법 문제 풀 수도 있다.
선형모형은 CVXPY.curvature 에서 $affine$ 으로 나오기 때문이다.
이는 DCP rule 로 CVXPY 가 검사해서 나온 결과다. $affine$ 은 $convex$ 로 볼 수 있다.
따라서 선형모형은 DCP rule 을 만족하는 $convex$ 함수라고 볼 수 있다.
목적함수가 DCP rule 을 만족했으므로,
CVXPY를 이용해서 제한조건 있는 컨벡스 최적화를 해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import cvxpy as cp
# 최적화 해 찾을 변수
x_1 = cp.Variable()
x_2 = cp.Variable()
# 부등식 제한조건
f1 = -x_1 <= -100
f2 = -x_2 <= -100
f3 = x_1+2*x_2 <= 500
f4 = 4*x_1 +5*x_2 <= 9800
# 목적함수 지정
obj = cp.Minimize(-3*x_1-5*x_2)
# 최적화 문제 정의
prob = cp.Problem(obj, constraints=[f1, f2, f3, f4])
# 최적화 문제 계산 명령
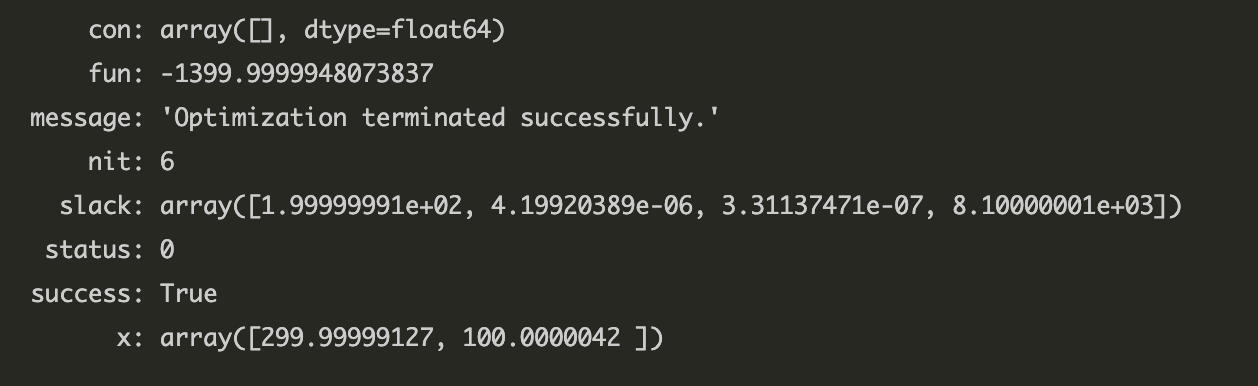
prob.solve()
print(prob.status)
print(x_1.value, x_2.value)
prob.solve()
결과 :
optimal
299.99, 100.00
-1400.00
선형계획법문제를 풀 수 있었다.
그리고 부등식 제한조건 $f1, f2$ 가 이미 $x_{1} \ge 0, x_{2} \ge 0$ 을 만족하고 있기 때문에 따로 지정하지 않아도 된다.
CVXOPT 이용해서 선형계획법 문제 풀기
앞에서 선형계획법 문제를 ‘제한조건 있는 컨벡스 최적화 문제’로 재정의하고, 푸는 것이 가능했다.
CVXPY 처럼 CVXOPT 도 컨벡스 최적화를 위한 패키지였다.
그러면 CVXOPT 를 통해서도 선형계획법 문제를 풀 수 있을 것이다.
마침 CVXOPT 에는 선형계획법 문제를 해결할 수 있는 solver.lp() 명령이 있다.
이 명령을 이용해서 선형계획법 문제를 풀어보자.
1
2
3
4
5
6
# cvxopt로 선형계획법 문제 풀기
c = matrix(np.array([-3.0,-5.0]))
A = matrix(np.array([[-1.0,0.0],[0.0,-1.0],[1.0,2.0],[4.0,5.0]]))
b = matrix(np.array([-100.0, -100.0, 500.0, 9800.0]))
np.array(solvers.lp(c, A, b)['x'])
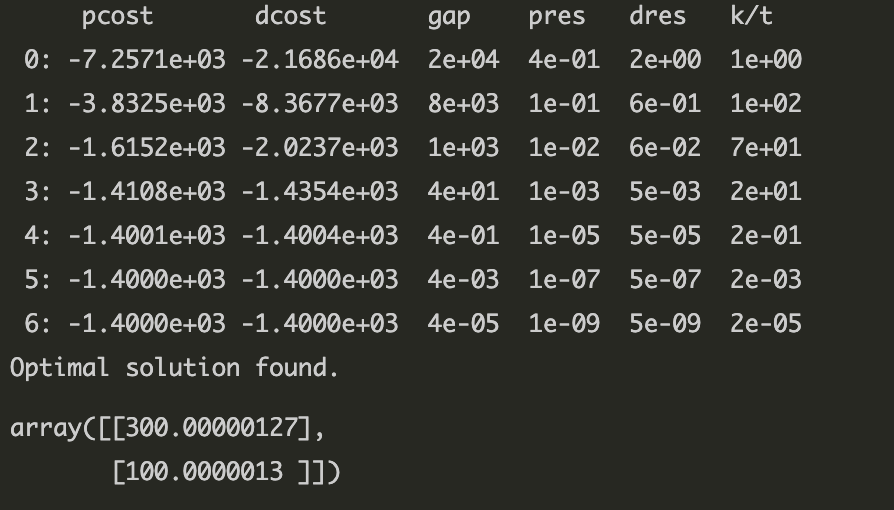
이처럼 CVXOPT 를 사용해서도 선형계획법 문제를 풀 수 있다.
*CVXPY든, CVXOPT 든 기본조건 $x \ge 0, y\ge 0$ 을 부등식 제한조건으로서 별도로 반영할 수도 있다. 각 패키지의 argument 를 잘 보자.
이차계획법 문제 (QP문제)
$Quadratic$ $Programming$
정의 :
‘일반화된 이차형식’을 등식/부등식 제한조건 걸고 최적화
목적함수
- $\frac{1}{2} x^{T}Qx + c^{T}x$
연립방정식 제한조건 (등식 제한조건)
- $Ax = b$
- $x \ge 0$
부등식 제한조건 (부등식 제한조건)
- $Ax \leq b$
- $x \ge 0$
목적함수인 일반화된 이차형식은
- 컨벡스 함수인 경우
- 넌 컨벡스 함수인 경우
두 가지 경우로 존재한다.
일반화된 이차형식 $\frac{1}{2} x^{T}Qx + c^{T}x$ 에서
행렬 $Q$ 가 양의 준정부호 이면 이차형식은 컨벡스 함수다. 이 경우 컨벡스 최적화 할 수 있다.
행렬 $Q$ 가 양의 준정부호가 아니면, 이차형식은 넌 컨벡스 함수다.
이때 함수는 다수의 국소 최저점 가질 수 있다. 이 경우 넌 컨벡스 최적화 해야 한다.
CVXOPT 를 이용해서 이차계획법 문제를 풀어보자
cvxopt 패키지의 solver.qp 명령을 이용해서 qp문제를 풀 것이다.
cvxopt 패키지는 ‘컨벡스 최적화’ 패키지다.
당연히 solver.qp() 명령도 컨벡스 최적화 명령일 것이다.
$\Rightarrow$ solver.qp() 명령은 이차형식 함수가 컨벡스 함수인 경우만 최적화 할 수 있다.
(행렬 $Q$ 가 양의 준정부호인 경우)
CVXOPT 로 이차계획법 문제를 푸는 예)
목적함수
$x_{1}^{2} + x_{2}^{2}$
등식 제한조건
$x_{1} + x_{2} -1 = 0$
일 때 목적함수를 이차형식 꼴 로 만들고, 이차계획법 문제로 최적화 하자.
목적함수는 다음과 같이 이차형식 꼴로 바꿀 수 있다.
$\frac{1}{2} [x_{1}, x_{2}][[2,0],[0,2]][x_{1}, x_{2}]^{T} + [0,0][x_{1}, x_{2}]^{T}$
제한조건은 다음과 같이 고칠 수 있다.
$[1,1][x_{1}, x_{2}]^{T} = 1$
따라서
$Q = [[2,0],[0,2]]$
$c = [0,0]^{T}$
$A = [1,1]^{T}$
$b = [1]$
이다.
목적함수가 일반화된 이차형식이므로, 이차계획법 문제로 생각하고 최적화 할 수 있다.
(그러면 이제 기본 조건 $x_{1} \ge 0$, $x_{2} \ge 0$ 도 만족시켜야 한다)
이때, 이차계획법 문제 푸는 데 CVXOPT의 solver.qp()를 이용하기 위해서는 이차형식의 행렬 $Q$ 가 양의 준정부호 여야 한다.
$Q = [[2,0],[0,2]]$ 였다.
$Q$ 를 이차형식 꼴로 만들면
$2x^{2}+2y^{2}$ 가 된다.
$x \ne 0$ , $y \ne 0$ 이므로,
$2x^{2}+2y^{2}$ 는 항상 양수다.
$\Rightarrow 2x^{2}+2y^{2} > 0$
$Q$의 이차형식이 0 또는 양수가 되어야 하는 양의 준정부호 조건을 만족한다.
곧, 이 문제의 목적함수 이차형식은 컨벡스 함수다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def f(x, y) :
return x**2+y**2
xx = np.linspace(-10,10,400)
yy = np.linspace(-10,10,500)
X,Y = np.meshgrid(xx,yy)
Z = f(X,Y)
ax = plt.gca(projection='3d')
ax.plot_surface(X,Y,Z, linewidth=0.03, cmap='flare')
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
plt.title('$f = x_{1}**2+x_{2}**2$')
plt.show()

목적함수가 컨벡스 함수임을 확인했다.
이제 CVXOPT의 solver.qp() 명령으로 이차형식을 최적화 하자.
1
2
3
4
5
6
7
8
9
10
# 이차계획법 문제
from cvxopt import matrix, solvers
Q = matrix(np.array([[2.0,0.0],[0.0,2.0]]))
c = matrix(np.array([0.0,0.0]))
A = matrix(np.array([[1.0,1.0]]))
b = matrix(np.array([1.0]))
r = solvers.qp(Q,c,A=A,b=b)['x']
np.array(r)
최적해 : $array([[0.5], [0.5]])$
이 경우에는 최적해가 0.5, 0.5 라서 $x_{1} \ge 0 , x_{2} \ge 0$ 가 아무 영향도 미치지 못하기 때문에, 별도의 부등식 제한조건으로 취급하지 않았다.
하지만 만약 $x_{1} \ge 0 , x_{2} \ge 0$ 에 의해 최적해가 영향을 받는다면,
$x_{1} \ge 0 , x_{2} \ge 0$ 도 별도의 부등식 제한조건으로 생각하고 solvers.qp() 의 argument로 넣어줘야 한다.
*G, h
조건만 맞다면. 하나의 함수에 대해 여러가지 최적화 방법. 알고리듬을 사용할 수 있다
하나의 함수에 대해서 다양한 최적화 방법을 시도할 수 있다.
함수 $x_{1}^{2}+x_{2}^{2}$ 를 최적화 하기 위해 다양한 최적화 방법을 시도해보자.
고려할 제한조건은 $x_{1} + x_{2} -1 = 0$ 이다.
# 1. sp.optimize.minimize()
이 방법은 제한조건을 받지 않는다.
라그랑주 승수법을 써서 목적함수를 변형한 다음 위 알고리듬으로 최적화 하겠다.
$h = x_{1}^{2} + x_{2}^{2} + \lambda (x_{1} + x_{2} -1)$
변형된 목적함수 $h$ 를 $x_{1}, x_{2}, \lambda$ 로 편미분 한 뒤, 기울기 필요조건을 만족하는 $\lambda$ 를 찾자.
$\lambda = -1$
$\Rightarrow$
$h = x_{1}^{2} + x_{2}^{2} - (x_{1} + x_{2} -1)$
이 목적함수 $h$를 sp.optimize.minimize() 명령에 넣어 최적화 하자.
1
2
3
4
5
6
7
# 하나의 함수에 여러가지 최적화 방법. 알고리듬을 쓸 수 있다.
# 1. sp.optimize.minimze()
def pf(x) :
return x[0]**2+x[1]**2-(x[0]+x[1]-1)
sp.optimize.minimize(pf, np.array([0,3]))
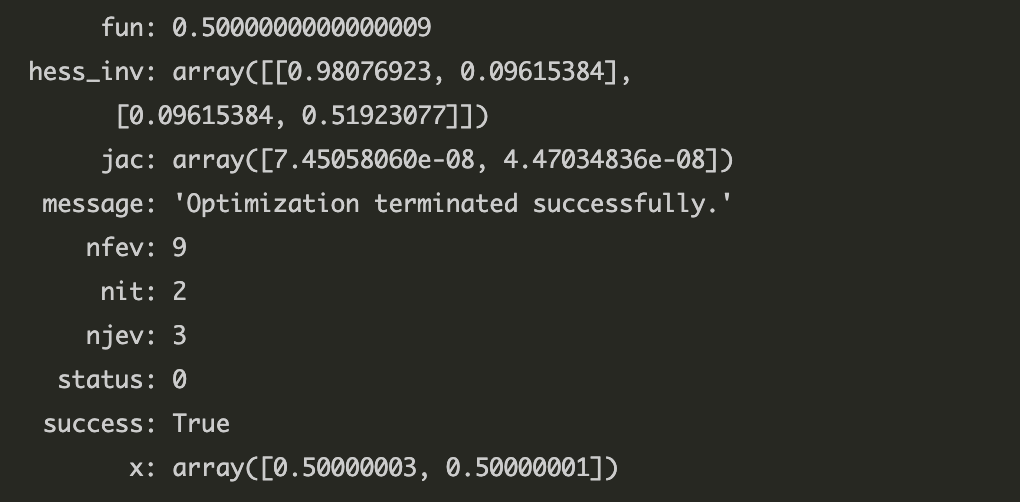
최적화에 성공했다. 최적해는 $[0.5, 0.5]$ 다.
총평 : 굳이 목적함수 변형 안 하고 라그랑주 승수법으로 $x_{1}, x_{2}$ 를 수기 계산하는 게 더 빨랐을 것이다.
# 2. fmin_slsqp()
이번에는 fmin_slsqp() 명령으로 제한조건 최적화를 바로 하겠다.
목적함수 : $x_{1}^{2}+x_{2}^{2}$
제한조건 : $x_{1} + x_{2} -1 = 0$
이다.
1
2
3
4
5
6
7
8
9
10
11
# 2. 제한조건 최적화
# 목적함수
def pf(x) :
return x[0]**2+x[1]**2
# 등식 제한조건
def con(x) :
return x[0]+x[1]-1
# 최적화
sp.optimize.fmin_slsqp(pf, np.array([1,2]), eqcons=[con])
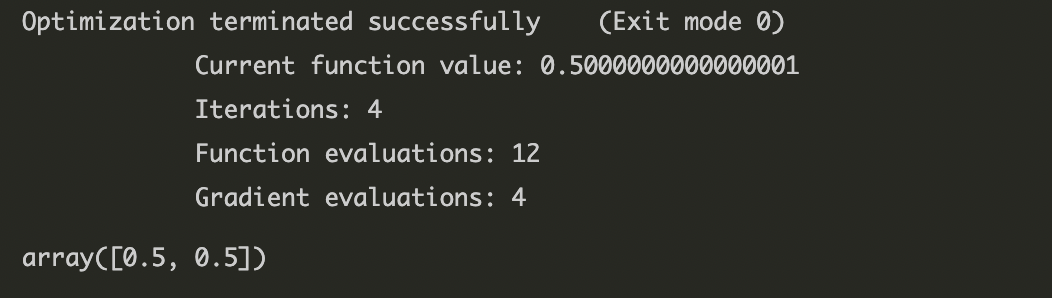
이번에도 최적화에 성공했다.
최적해는 역시 $[0.5, 0.5]$ 다.
총평 : 첫번째 방법보다는 훨씬 수월하고, 사람이 직접 해야 할 계산이 적어서 편했다.
# 3. CVXPY 를 이용한 컨벡스 최적화
이번에는 CVXPY 를 이용한 컨벡스 최적화를 해보자.
먼저, CVXPY 는 컨벡스 함수 이면서 DCP rule을 만족하는 녀석들만 컨벡스 최적화 하는 패키지다.
따라서, 내가 최적화 하려는 목적함수 $x_{1}^{2}+x_{2}^{2}$ 가
컨벡스함수
DCP rule 만족
1,2 조건을 만족해야만 CVXPY로 컨벡스 최적화 할 수 있다.
앞에서 봤듯이, 이 함수는 컨벡스 함수다.
- 이차형식 꼴로 고쳤을 때, 행렬 $Q$ 가 양의 준정부호 였다.
- 그래프로 그려보면 컨벡스 함수 형상이다.

컨벡스 함수임을 확인했으니, 이제 DCP rule을 만족하는 지 봐야한다.
(DCP rule 은 컨벡스 필요조건으로, DCP rule 을 만족하면 모두 컨벡스 함수이지만, DCP rule 을 만족하지 않는 컨벡스 함수들도 있다)
1
2
3
4
# 목적함수
obj = cp.Minimize(x**2+y**2)
# 목적함수가 컨벡스 최적화 가능한가? (목적함수가 볼록함수인가, 오목함수인가?)
print(obj.is_dcp())
결과 : True
목적함수가 DCP rule 을 만족한다.
그러면 이제 목적함수를 CVXPY 로 컨벡스 최적화 할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# x**2+y**2 는 볼록함수다.
# 3. cvxpy 를 이용한 컨벡스 최적화
import cvxpy as cp
x = cp.Variable()
y = cp.Variable()
# 목적함수
obj = cp.Minimize(x**2+y**2)
# 목적함수가 컨벡스 최적화 가능한가? (목적함수가 볼록함수인가, 오목함수인가?)
print(obj.is_dcp())
# 볼록함수다.
# 제한조건
cons = [x+y-1 == 0]
# 최적화 문제 정의
prob = cp.Problem(obj, constraints=cons)
# 제한조건 감안했을 때, 볼록함수 최적화가 가능한가?
print(prob.is_dcp()) # 가능하다.
prob.solve(), x.value, y.value
결과 :
True
True
(0.5, 0.5)
제한조건을 감안해도 위 최적화 문제를 컨벡스 문제로 풀 수 있었다.
최적해는 마찬가지로 $[0.5, 0.5]$ 다.
총평 : 주어진 목적함수가 컨벡스 함수인지, DCP rule 을 만족하는지 확인해야 하는 점이 번거롭긴 했지만, 직관적인 심볼릭 연산이 가능해서 편했다.
# 4. CVXOPT 를 이용한 최적화
앞에서 목적함수 $x_{1}^{2}+x_{2}^{2}$ 가 일반화된 이차형식(quadratic form) 으로 바뀔 수 있다는 걸 봤다.
또, 이차형식의 행렬 $Q$ 는 양의 준정부호 조건을 만족했다.
따라서 목적함수는 이차형식 꼴인 컨벡스 함수로도 생각할 수 있다.
CVXOPT 의 solver.qp() 명령은 목적함수(이차형식)가 컨벡스 함수인 이차계획법 문제를 푸는 명령이었다.
문제의 목적함수가 이차형식 이면서 컨벡스 함수이기 때문에, CVXOPT solver.qp() 명령으로 주어진 목적함수를 최적화 할 수 있다.
이 경우 문제가 이차계획법 문제가 되었기 때문에 고려해야 할 조건으로 $x_{1} \ge 0, x_{2} \ge 0$ 이 추가된다.
1
2
3
4
5
6
7
8
9
10
11
# x**2+y**2 는 일반화된 이차형식으로 바꿀 수 있다.
# 4. cvxopt를 이용해 이차계획법으로 풀기
from cvxopt import matrix, solvers
Q = matrix(np.array([[2.0,0.0],[0.0,2.0]]))
c = matrix(np.array([0.0,0.0]))
A = matrix(np.array([[1.0,1.0]]))
b = matrix(np.array([1.0]))
np.array(solvers.qp(Q, c, A=A, b=b)['x'])
결과 : $[0.5, 0.5]$
최적화에 성공했다.
$x_{1} \ge 0, x_{2} \ge 0$ 조건은 최적화에 영향 미치지 못했기 때문에, 없는 거나 다름 없었다. 따라서 따로 argument 를 명시하지 않았다.
총평 : 목적함수가 일반화된 이차형식 꼴을 만족하는지, 그리고 행렬 $Q$ 가 양의 준정부호 인지 확인해야 하는 점이 번거로웠다.
