상호정보량 (Mutual Information)
- 정의 : 확률변수 $X$ 와 $Y$ 사이 상관관계 정도 나타내는 값
피어슨 상관계수 대용으로 쓸 수 있다.
피어슨 상관계수는 비선형 상관관계 나타내지 못한다.
하지만 상호정보량은 선형, 비선형 상관관계 모두 나타낼 수 있다.
$p(x,y)$와 $p(x)p(y)$의 쿨백-라이블러발산값이다.
$MI[X,Y] = KL(p(x,y)\Vert p(x)p(y))$
확률변수 X,Y 사이 상관관계 정도가 강할 수록 상호정보량 증가
확률변수 X,Y 사이 상관관계 정도가 약할 수록 상호정보량 감소
두 확률변수 독립이면 쿨백-라이블러 발산값이 0 된다. 따라서 상호정보량값도 0 된다.
- $MI[X,Y] = H[X]-H[X\vert Y]$
- $MI[X,Y] = H[Y]-H[Y\vert X]$
이산확률변수 사이 상호정보량 계산
- sklearn.metrics 패키지의 mutual_info_score()
1
from sklean.metrics import mutual_info_score
mutual_info_score(X 데이터 배열, Y 데이터 배열)
X,Y 순서 바뀌어도 상관 없다.
이산확률변수 사이 상호정보량 계산 예 )
데이터사이언스스쿨 713p 뉴스그룹 카테고리 예제
1번부터 2.3만번 뉴스 키워드 확률변수가 있다.
각 확률변수는 1~k 사이 정수를 데이터로 내놓는 ‘카테고리확률변수’다.
각 확률변수는 1785개씩 데이터를 갖고 있다.
한편
뉴스그룹카테고리 확률변수가 있다. 이 확률변수는 0,1,2 만을 내놓는 ‘카테고리확률변수’다.
뉴스그룹카테고리 확률변수 역시 1785개 데이터를 갖고 있다.
1번 - 뉴스그룹 확률변수 , 2번 - 뉴스그룹 확률변수 … 이런 식으로 해서 각 키워드 확률변수와 뉴스그룹 확률변수 사이 상관관계가 있는지, 상호정보량 값으로 알아보자.
상호정보량 값이 크다면(상관관계가 크다면) 키워드 확률변숫값을 알 때, 뉴스그룹 키워드 확률변숫값에 대한 대략적 정보를 얻을 수 있을 것이다.
바꿔말하면, 키워드가 몇 번 나왔는지 보면 이 뉴스 기사가 어떤 카테고리에 속하는 뉴스 기사 인지 대강 예측할 수 있다는 말이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 이산확률변수 간 상호정보량 계산
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import mutual_info_score
categories = ['rec.autos', 'sci.med', 'rec.sport.baseball']
newsgroups = fetch_20newsgroups(subset='train', categories=categories)
vect = CountVectorizer(stop_words='english', token_pattern = '[a-zA-Z]+')
X = vect.fit_transform(newsgroups.data).toarray() # 2.3만개 카테고리 확률변수, 각각 확률변숫값 1785개씩
y = newsgroups.target # 뉴스그룹 카테고리확률변숫값(0,1,2)
mi = [mutual_info_score(X[:,i], y) for i in range(X.shape[1])] # i번 키워드 확률변수와 뉴스그룹카테고리확률변수 간 상호정보량 값들
plt.stem(mi)
plt.title('뉴스그룹 카테고리확률변수와 i번 키워드 카테고리확률변수 사이의 상호정보량')
plt.xlabel('키워드 번호')
plt.show()

결과를 해석해보자.
위 코드에서 X는 0번~ 2.3만번 까지 키워드 ‘카테고리 확률변수’ 들이다. 각각 1785개씩 데이터를 가지고 있다. 따라서 1785 * 2.3만 의 행렬 형태다.
이 행렬에서 각 열과 뉴스그룹카테고리 확률변수 데이터를 가지고 상호정보량을 계산할 것이다.
한편 y는 뉴스그룹카테고리 확률변수다. 0,1,2 만을 표본으로 내놓는 카테고리확률변수다.
1
mi = [mutual_info_score(X[:,i], y) for i in range(X.shape[1])]
이제 이 코드를 통해 1번 키워드 - 뉴스그룹, 2번 키워드 - 뉴스그룹, 3번 키워드 … 이런 식으로 각 확률변수 간 상호정보량 값을 계산해서 mi 리스트 안에 담는다.
이 값들은 ‘각 키워드 별 뉴스그룹과의 상호정보량’ 값들이다.
각 상호정보량 값들의 인덱스 넘버는 키워드 번호와 같다. i번째 상호정보량 값은 i번째 키워드의 (뉴스그룹과의) 상호정보량 값이다.
키워드 별 상호정보량 값들을 stem 플롯으로 나타낸 것이 위 이미지와 같다.
stem 플롯에서 상호정보량 값이 높을 수록 뉴스그룹카테고리와 상관관계가 강한 키워드다.
바꿔말하면, 키워드 빈도를 알 때 뉴스그룹 카테고리가 뭘 지 대강 예측 가능한 키워드다.
가장 상호정보량 값이 높은, 상위 10개 키워드만 뽑아보자.
1
2
3
inv_vocabulary = {v:k for k, v in vect.vocabulary_.items()} # 0~2.3만번 키워드
idx = np.flip(np.argsort(mi))
[inv_vocabulary[idx[i]] for i in range(10)]
inv_vocabulary는 번호 : 키워드 이름 으로 구성된 딕셔너리다. 각 번호는 키워드 번호다.
1
idx = np.flip(np.argsort(mi))
이 코드를 통해 상호정보량 값들이 작은 순서대로 인덱스 번호들을 따고, 앞뒤 순서를 다시 뒤집는다. 곧, 상호정보량 값들을 내림차순 정렬시킨 뒤 각 값들을 mi 리스트 에서 할당된 인덱스 번호로 바꿨다.
idx 리스트는 이제 상호정보량 값이 가장 큰 키워드~ 가장 작은 키워드 순으로 정렬되었다.
1
[inv_vocabulary[idx[i]] for i in range(10)]
마지막 코드를 통해, 키워드 사전인 inv_vocabulary 딕셔너리에서 상호정보량 상위 10개 키워드를 영단어 형태로 뽑아낸다.
[‘car’, ‘baseball’, ‘cars’, ‘team’, ‘game’, ‘games’, ‘season’, ‘players’, ‘geb’, ‘gordon’]
예컨대 가장 상호정보량 값이 높았던 단어, car의 경우, 뉴스 기사에 ‘car’가 몇 번 등장했는지 알면 이 뉴스 기사가 어떤 카테고리에 속하는 뉴스 기사 일 지 대강 예측이 가능하다는 말이다.
최대정보 상관계수 (Maximul information coefficient : MIC)
- 연속확률변수 X,Y 사이 상관관계 정도를 나타내는 값.
- 상호정보량의 일종이다.
- max(상호정보량)
상호정보량을 계산하려면 확률밀도함수가 필요하다. 연속확률변수에서 나온 데이터를 가지고 이 확률밀도함수를 추정 하는데, 데이터를 여러 단위 구간으로 쪼개서 단위 별로 확률밀도함수를 여러 개 추정한다.
그리고 각각 확률밀도함수로 각각 상호정보량 값을 구한다.
이 중에서 ‘가장 큰 상호정보량 값’을 골라서 정규화 한 값이 ‘최대정보 상관계수’다.
연속확률변수 사이 상호정보량 계산
minepy 패키지를 이용해서 MIC 값 계산할 수 있다.
1
2
from minepy import MINE
mine = MINE()
1. mine.compute_score(x데이터 배열, y데이터 배열)
2. mine.mic()
- x 데이터 배열과 y 데이터 배열 넣는 순서는 상관 없다.
- 2번 mine.mic() 명령을 내려야 최대정보 상관계숫값 반환한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
from minepy import MINE
mine = MINE()
plt.figure(figsize=(8,6))
n = 500
plt.subplot(231)
x1 = np.random.uniform(-1,1,n)
plt.scatter(x1, x1)
mine.compute_score(x1, x1)
plt.title(f'MIC = {np.round(mine.mic(),2)}')
plt.subplot(232)
x2 = np.random.normal(size=n)
y2 = x2 + x1
plt.scatter(x2, y2)
mine.compute_score(x2, y2)
plt.title(f'MIC = {np.round(mine.mic(),2)}')
plt.subplot(233)
x3 = np.random.uniform(-1,1,n)
y3 = 2*x3**5+np.random.uniform(-1,1,n)
plt.scatter(x3, y3)
mine.compute_score(x3, y3)
plt.title(f'MIC = {np.round(mine.mic(), 2)}')
plt.subplot(234)
x4 = np.random.uniform(-1,1,n)
y4 = x4**8+x1/2
plt.scatter(x4, y4)
mine.compute_score(x4, y4)
plt.title(f'MIC = {np.round(mine.mic(),2)}')
plt.subplot(235)
x5 = np.random.uniform(-1,1,n)
y5 = 4*(x5**2-0.5)**3+np.random.uniform(-1,1,n)/5
plt.scatter(x5, y5)
mine.compute_score(x5, y5)
plt.title(f'MIC = {np.round(mine.mic(),2)}')
plt.subplot(236)
x6 = np.random.uniform(-1,1,n)
y6 = (x6**2 + np.random.uniform(-1/7,1/7, n))*np.array([-1,1,])[np.random.random_integers(0,1,size=n)]
plt.scatter(x6, y6)
mine.compute_score(x6,y6)
plt.title(f'MIC = {np.round(mine.mic(),2)}')
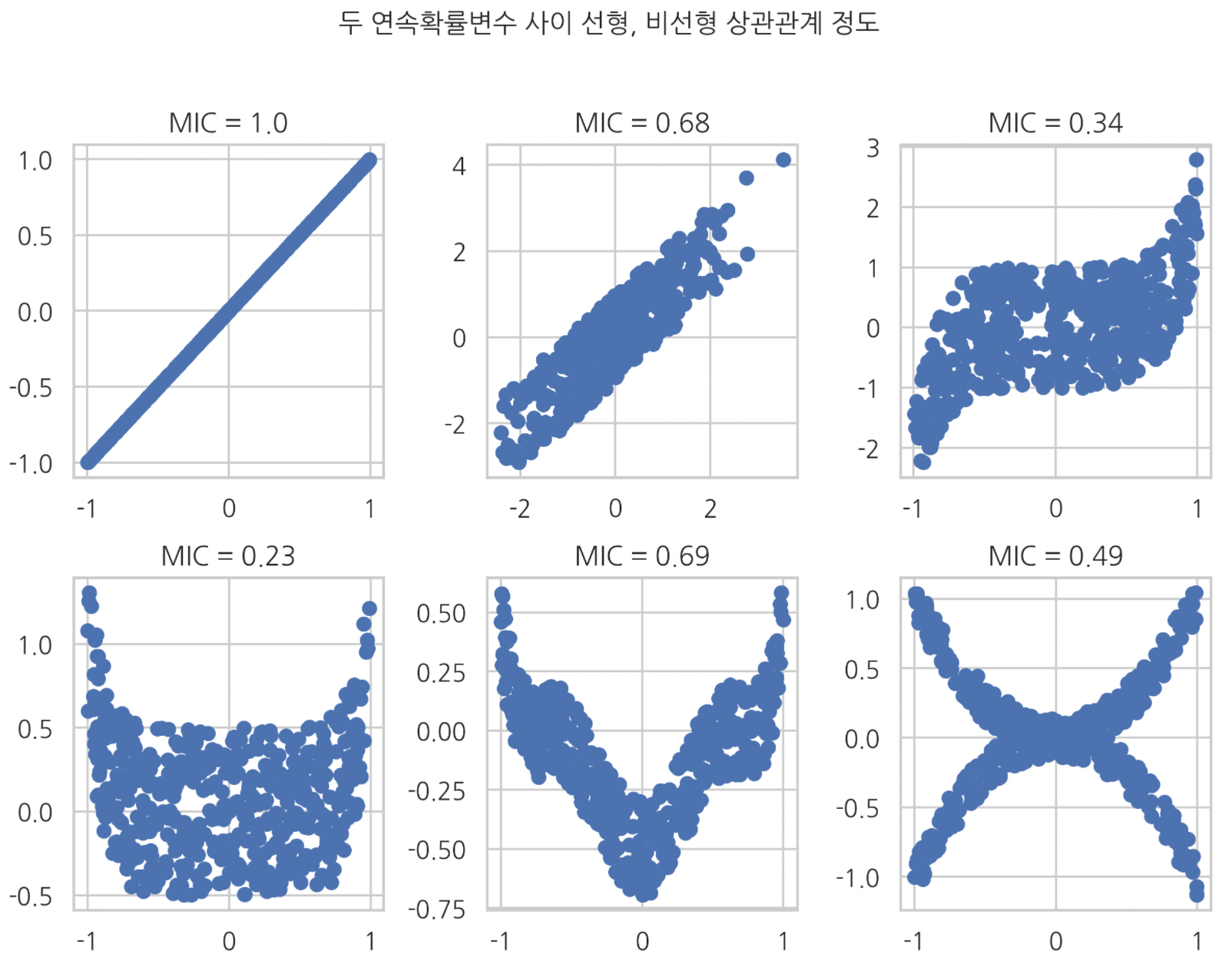
plt.suptitle('두 연속확률변수 사이 선형, 비선형 상관관계 정도', y=1.03)
plt.tight_layout()
plt.show()