최적화
정의 :
함수 출력을 최대 또는 최소로 만드는 ‘최적 입력 찾기’
- 보통, 최적화 문제 = 최소화 문제 다.
최대화 하고 싶은 어떤 함수 $f(x)$ 를 뒤집어서 $-f(x)$ 에 대해 최소화 문제를 풀면 결국 $f(x)$ 의 최대화 문제를 푼 것과 같다.
$\Rightarrow$ $-f(x)$ 의 최소해는 함수 $f(x)$ 의 최대해와 같다.
최적화 목적함수
정의 :
최적화 대상이 되는 함수를 ‘목적함수’ 라고 한다.
예) 성능함수, 손실함수, 오차함수, 등
최적화 방법 - 그리드 서치 방법
정의 :
최적값이 있음직한 일정 구간을 함수에 직접 넣어보는 방법.
- 직접 넣어보고 함수 출력이 최소화되는 입력값을 찾는다.
특징 :
노가다. 비효율적이다.
특히 입력값이 많아지면 일일이 입력값-출력값 쌍을 계산해야 된다.
예 :
1차원 목적함수 최적화(최소화)
1
2
3
4
5
6
7
8
9
10
11
def f(x) :
return (x-2)**2+2
xx = np.linspace(-1, 4, 1000)
plt.plot(xx, f(xx))
plt.plot(xx[np.argmin(f(xx))], f(xx)[np.argmin(f(xx))], 'ro', markersize=10)
plt.ylim(0, 10)
plt.xlabel('$x$')
plt.title('1차원 목적함수, 최적해 : $x=2$, 최저출력 : $y=2$')
plt.show()
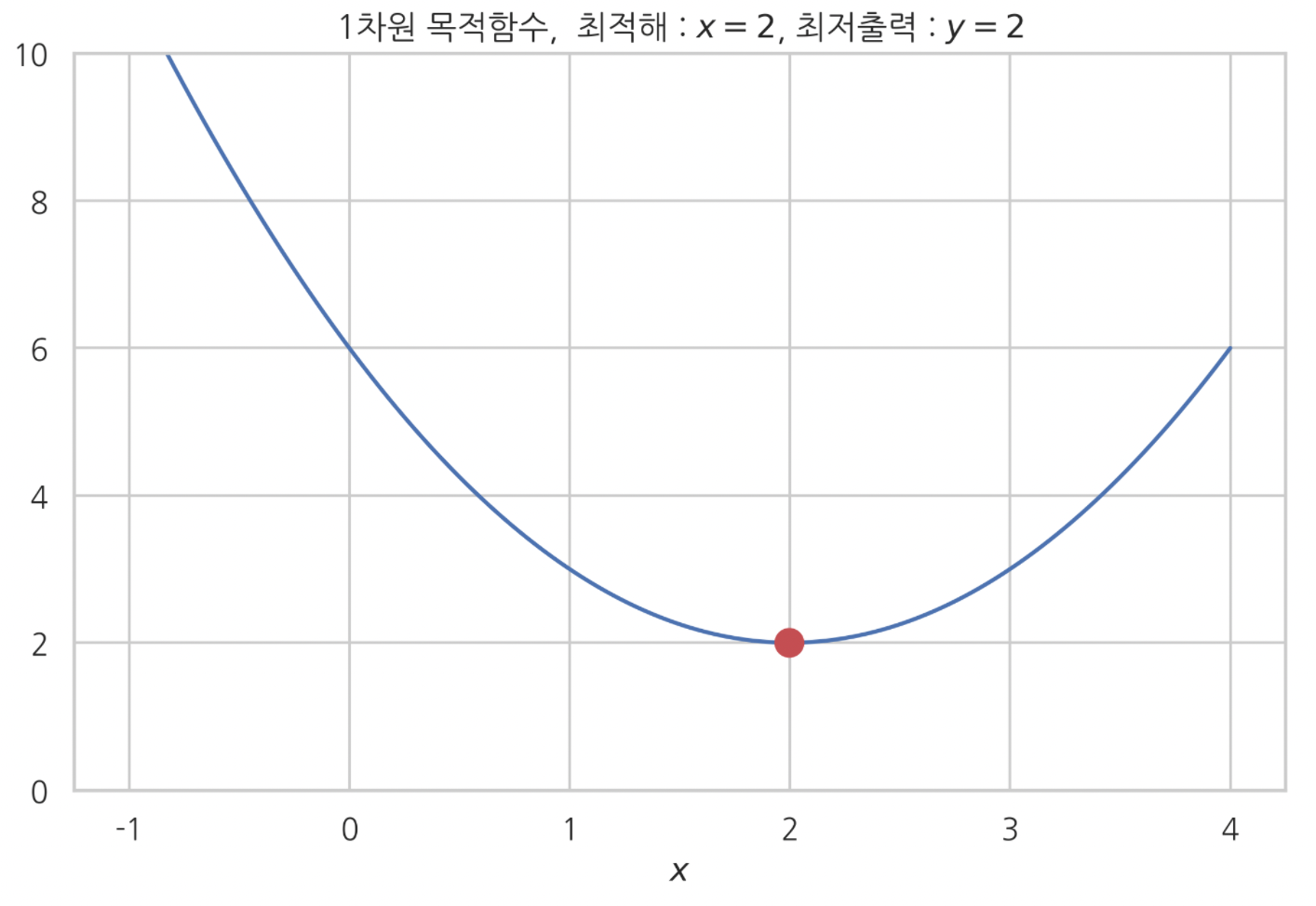
위 그래프는
그리드 서치 방법으로 1차원 함수 최적화 하는 과정을 시각화 한 것이다.
$-1$, $4$ 사이 구간에서, $1000$ 개 입력값을 함수 $(x-2)^{2}+2$ 에 일일이 넣었다.
그리고 $1000$ 개 입력에 대응되는 $1000$ 개 출력값을 하나하나 찾았다.
그래프는 찾은 $1000$ 개 출력값들을 2차원 벡터공간 상에 일일이 점으로 찍은 것 뿐이다.
$-1, 4$ 사이 구간 입력 $1000$ 개를 넣어 본 결과, $x=2$ 에서 가장 출력값이 작았다.
따라서 함수 출력을 최소화 하는 최적 입력값은 $x=2$ 이다.
최적화 방법 - 수치적 최적화 방법
정의 :
최소 시도 횟수로 최적화를 성공시키고자 하는 게 목표인 최적화 방법.
수치적 최적화 알고리듬 :
- 현재 위치가 최적점(최소점) 인지 판단하는 알고리듬
- 현재 위치가 최적점이 아닐 때, 옮겨 갈 다음 위치를 선정하는 알고리듬
기울기 필요조건 (최적화 필요조건)
정의 :
최적해에서, 1차 도함숫값(기울기)은 0이다.
- 최소해. 최대해 모두 1차 도함숫값이 0 나와야 한다.
- 2차 도함숫값이 양수면 확실한 최소점
- 2차 도함숫값이 음수면 확실한 최대점이다.
현재 위치가 최적점인지 판단하는 알고리듬 이다.
최대경사법(최급강하법)
현재 위치가 최적점이 아닐 때, 옮겨 갈 다음 위치를 선정하는 알고리듬이다.
정의 :
기울기가 가장 크게 감소하는 방향으로 이동하는 수치적 최적화 알고리듬.
$x_{n+1} = x_{n} - \mu\nabla{f(x_{n})}$
- $\mu$ 는 ‘스텝사이즈’라고 한다. 위치 얼만큼 이동할 건지 거리를 결정짓는다.
단변수 함수
- $-\mu$ $\times$ $\nabla{f(x_{n})}$ 만큼 $x$ 축 따라 계속 이동하다가, $x_{n+1} = x_{n}$ 이 되면(기울기가 $0$ 되면) 이동 멈춘다.
다변수 함수
- 각 점의 그레디언트 벡터 반대방향으로 $- \mu\nabla{f(x_{n})}$ 벡터의 길이만큼 이동한다.
- 다음 위치는 $- \mu\nabla{f(x_{n})}$ 벡터가 가리키는 지점이다.
참고)
다변수 함수에서
점의 이동 거리가 $- \mu\nabla{f(x_{n})}$ 벡터 길이인 이유는
$x_{n+1} - x_{n} = - \mu\nabla{f(x_{n})}$
때문이다.
단변수 함수 최대경사법 알고리듬으로 최적화 하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def f(x) :
return (x-2)**2+2
def fprime(x) :
return 2*x-4
xx = np.linspace(-1,4,100)
plt.plot(xx, f(xx)) # 함수 f
# 최적화 해보자. x=0에서 시작, 스텝사이즈 mu = 0.4
mu = 0.4
def next_step(x, mu) :
x_1 = x-mu*fprime(x)
return (x_1, f(x_1))
plt.plot(k, f(k), 'go', markersize=10)
plt.plot(xx, fprime(k)*(xx-k)+f(k), 'b--')
plt.text(k, f(k)+0.7, '1차 시도')
next_ = next_step(0, mu)
plt.plot(next_[0], next_[1], 'go', markersize=10)
plt.plot(xx, fprime(next_[0])*(xx-next_[0])+f(next_[0]), 'b--')
plt.text(next_[0], next_[1]+0.6, '2차 시도')
next_ = next_step(next_[0], mu)
plt.plot(next_[0], next_[1], 'go', markersize=10)
plt.plot(xx, fprime(next_[0])*(xx-next_[0])+f(next_[0]), 'r--')
plt.text(next_[0], next_[1]-1.4, '3차 시도')
plt.title('최급강하법을 이용한 1차함수 최적화')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.ylim(0, 10)
plt.show()
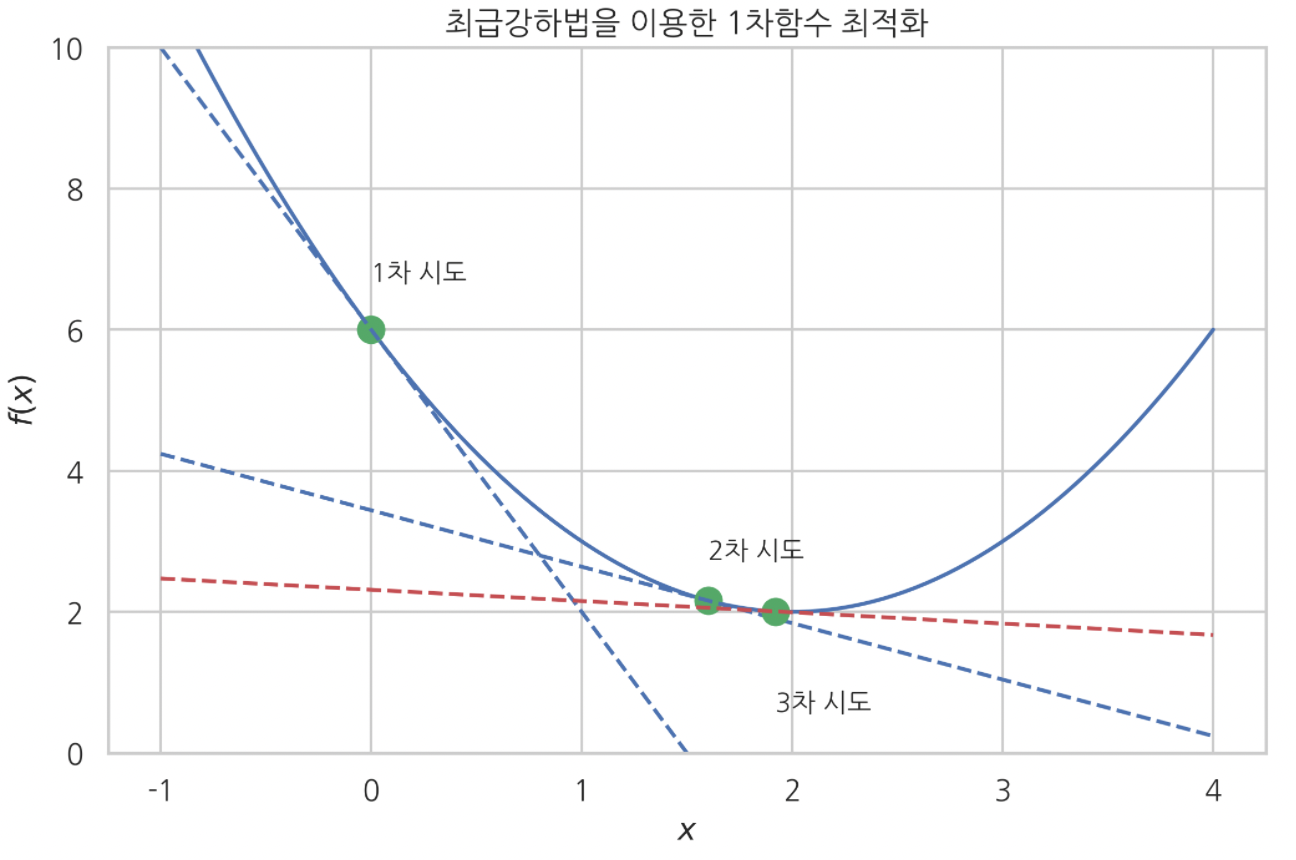
다변수 2차원 함수 최대경사법 알고리듬으로 최적화 하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(-4, 4, 600)
yy = np.linspace(-3, 3, 400)
X,Y = np.meshgrid(xx, yy)
Z = rosenbrook(X,Y)
plt.contourf(X,Y,Z, levels=np.logspace(-1,3,10), alpha=0.3)
plt.contour(X,Y,Z, colors='green', levels=np.logspace(-1,3,10))
a = -1
b = -1
mu = 8e-4
def next_level(a,b) :
return np.array([a,b]) - mu*gradient(a,b)
vec_list = []
for i in range(3000) :
vec_list.append((a,b))
result = next_level(a,b)
a = result[0] ; b = result[1]
for a, b in vec_list :
plt.arrow(a,b, -mu*0.95*gradient(a,b)[0], -mu*0.95*gradient(a,b)[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw=2)
plt.plot(a,b, 'ro', markersize=3)
plt.xlim(-3,3)
plt.ylim(-2,2)
plt.xticks(np.linspace(-3,3,7))
plt.yticks(np.linspace(-2,2,5))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.suptitle('2차원 로젠브록함수 최급강하법으로 최적화 과정', y=1.03)
plt.title('그레디언트 벡터 반대방향 따라서 최적점 찾아가는 중')
plt.annotate('',xy=[1,1], xytext=[1.3,1.3], arrowprops={'facecolor':'black'})
plt.text(1.2, 1, '최적점')
plt.plot(1,1, 'ro', markersize=10)
plt.show()
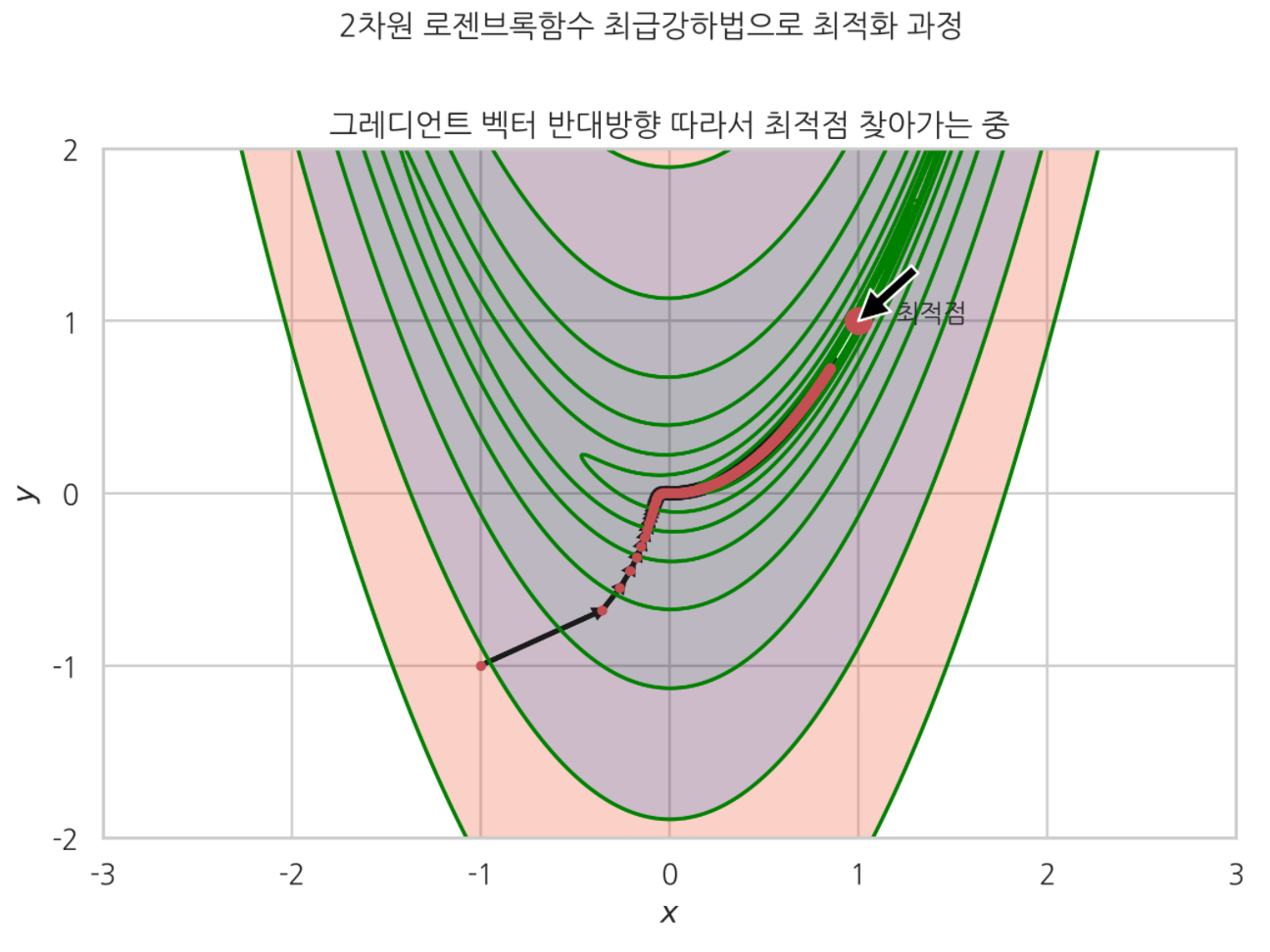
최적화 알고리듬 테스트에 많이 사용되는. 2차원 로젠브록함수를 최대경사법 알고리듬으로 최적화 했다.
위 경우는 $[-1,-1]$ 에서 최적화를 시작한 경우다. 스텝사이즈 $8e-4$ 에서 그레디언트 벡터 반대방향을 따라 서서히 최적점에 수렴해가고 있는 모습을 볼 수 있었다.
최대경사법 단점 1 : 스텝사이즈가 최적화를 방해한다
스텝사이즈 크기가 최적화에 방해될 수 있다.
스텝사이즈 크기가 너무 크면 최적해에 제대로 수렴 안 할 수 있다.
예) 스텝사이즈 : 1.4 (너무 큰 스텝사이즈)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
mu = 1.4 # 너무 큰 스텝사이즈
def f(x) :
return (x-2)**2+2
def fprime(x) :
return 2*x-4
xx = np.linspace(-8,10,100)
plt.plot(xx, f(xx))
plt.plot(0, f(0), 'go', markersize=10)
plt.text(0, f(0)+0.9, '1차 시도')
plt.plot(xx, fprime(0)*(xx-0)+f(0), ls='--', c='b')
print(f'1차 시도, x값 : {0}, 기울기 값 : {fprime(0)}')
next_ = next_step(0, mu)
plt.plot(next_[0], next_[1], 'ro', markersize=10)
plt.text(next_[0]-0.5, next_[1]+5, '2차 시도')
plt.plot(xx, fprime(next_[0])*(xx-next_[0])+f(next_[0]), ls='--', c='b')
print(f'2차 시도, x값 : {np.round(next_[0],2)}, 기울기 값 : {np.round(fprime(next_[0]),2)}')
next_ = next_step(next_[0], mu)
plt.plot(next_[0], next_[1], 'bo', markersize=10)
plt.text(next_[0], next_[1], '3차 시도')
plt.plot(xx, fprime(next_[0])*(xx-next_[0])+f(next_[0]), ls='--')
print(f'3차 시도, x값 : {np.round(next_[0],2)}, 기울기 값 : {np.round(fprime(next_[0]),2)}')
plt.xlim(-8, 10)
plt.ylim(-100,100)
plt.suptitle('최급강하법을 이용한 1차 함수 최적화', y=1.01)
plt.title('스텝사이즈 $\mu$가 너무 커서(1.4) 오히려 최소점에서 멀어진 경우')
plt.show()
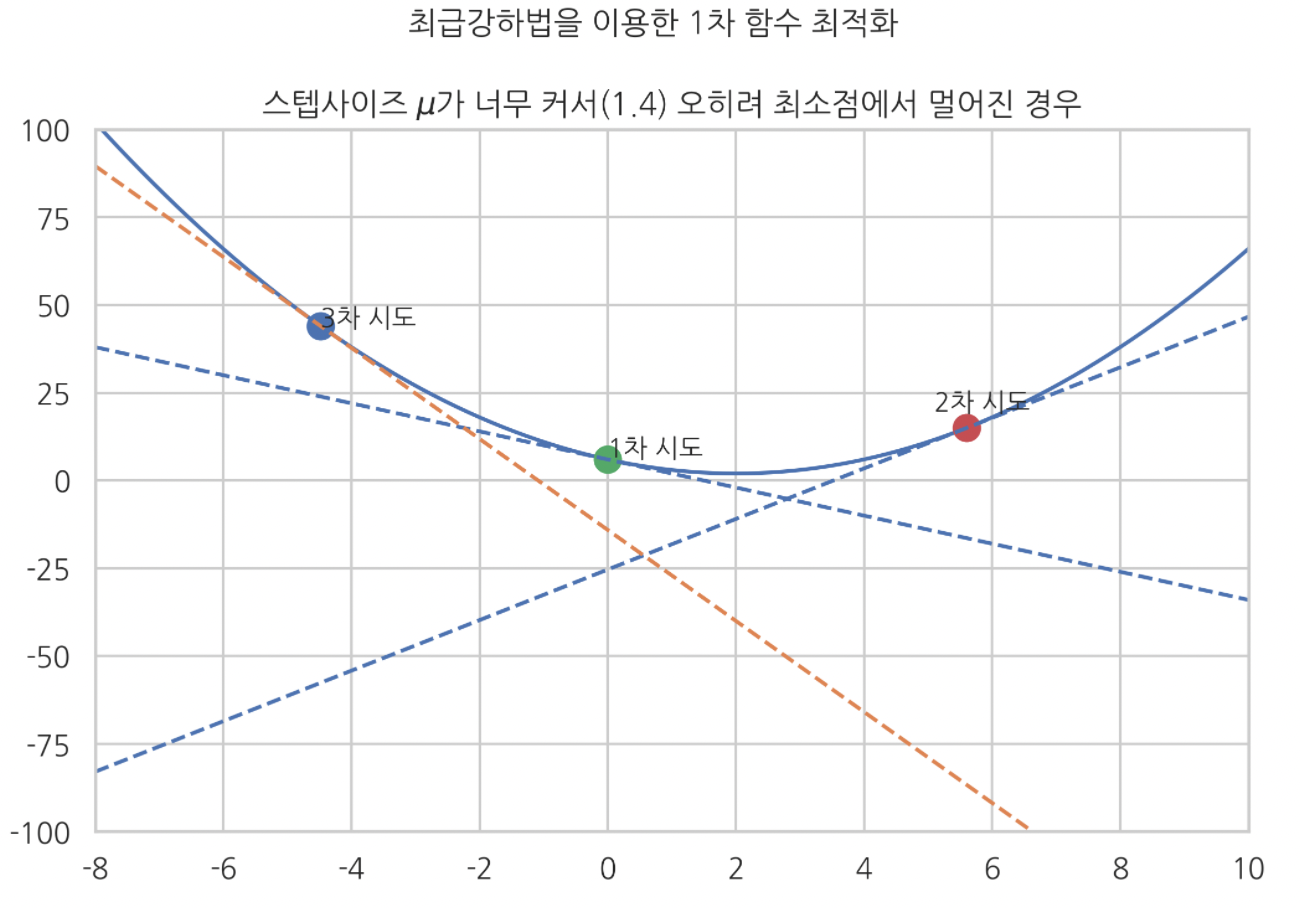
결과물을 보면, 스텝사이즈가 너무 커서 오히려 최저점에서 멀어진 것을 볼 수 있다.
곧, 스텝사이즈가 너무 크면 최적화에 방해가 된다.
한편,
스텝사이즈가 너무 작으면 최적점에 너무 느리게 수렴한다.
또한 최적점에 제대로 수렴 안 할 수도 있다.
아래 예는 스텝사이즈가 $1.8e-4$ 로, 너무 작은 예다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(0, 3, 500)
yy = np.linspace(0, 3, 500)
X,Y = np.meshgrid(xx, yy)
Z = rosenbrook(X,Y)
plt.contourf(X,Y,Z, alpha=0.3, levels=np.logspace(-1,4,20))
plt.contour(X,Y,Z, colors='green',levels=np.logspace(-1,4,20), alpha=0.2) # 로젠브록함수 계곡에 해당하는 지역
mu = 1.8e-4 # 스텝사이즈
a = 1.5
b = 1.5
for i in range(3000) :
plt.plot(a,b, 'ro', markersize=5)
plt.arrow(a, b, -0.95*mu*gradient(a, b)[0], -0.95*mu*gradient(a, b)[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw = 2)
next_step = np.array([a,b]) - mu*gradient(a,b)
a = next_step[0]
b = next_step[1]
plt.plot(1,1, 'bo', markersize=5)
plt.plot(a,b, 'ro', markersize=5)
plt.title('스텝사이즈가 너무 작아서 조금씩 이동하는 예')
plt.xlim(0,3)
plt.ylim(0,2)
plt.xticks(np.linspace(0,3,4))
plt.yticks(np.linspace(0,2,3))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
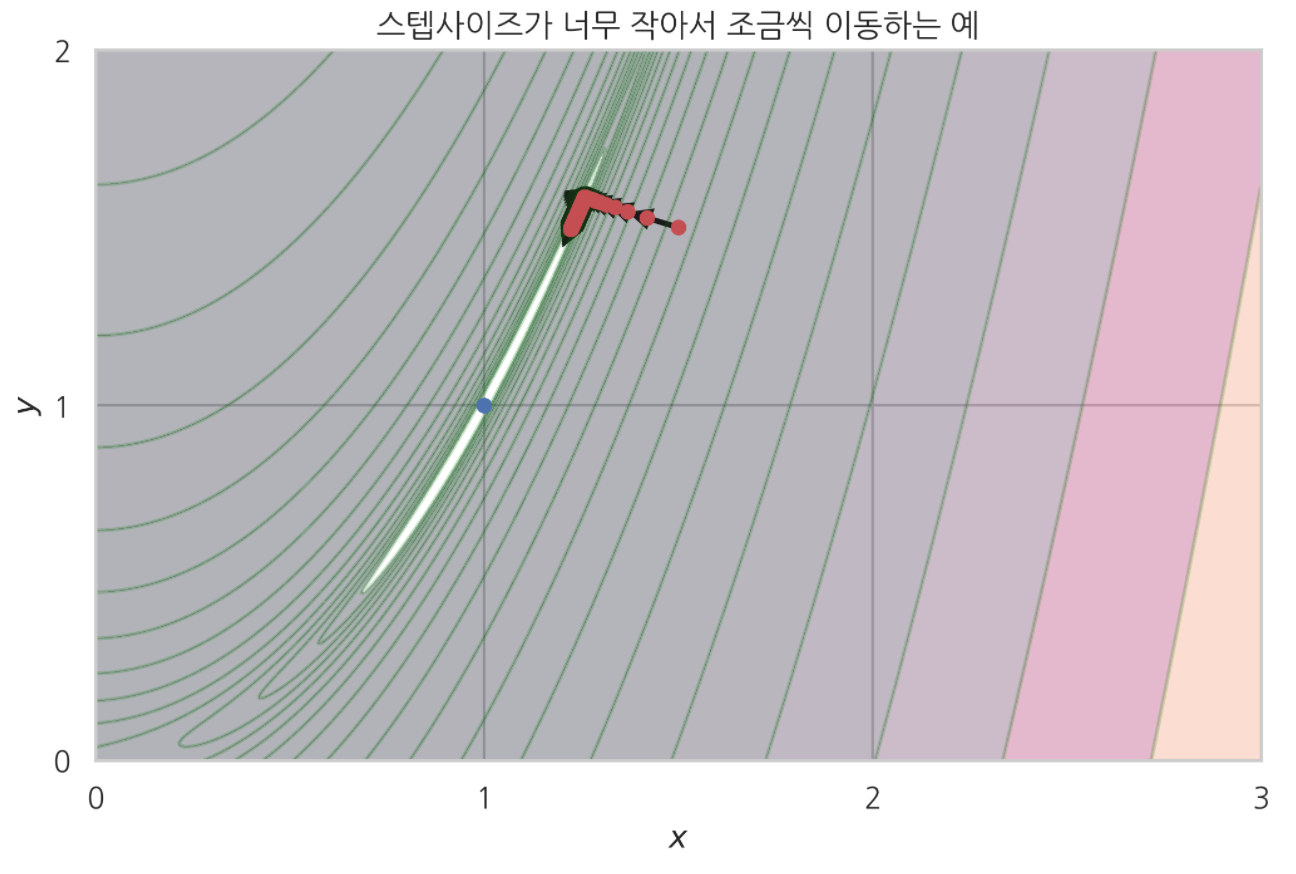
어느 세월에 파란 점(최소점)까지 도달하겠나 싶다.
한편 스텝사이즈가 위 경우보다 더 작으면, 3000번이나 이동했음에도 제대로 수렴 안 하는 경우도 있었다.
스텝사이즈 : $1.8e-6$ 인 경우
이동 횟수 : $3,000$ 번
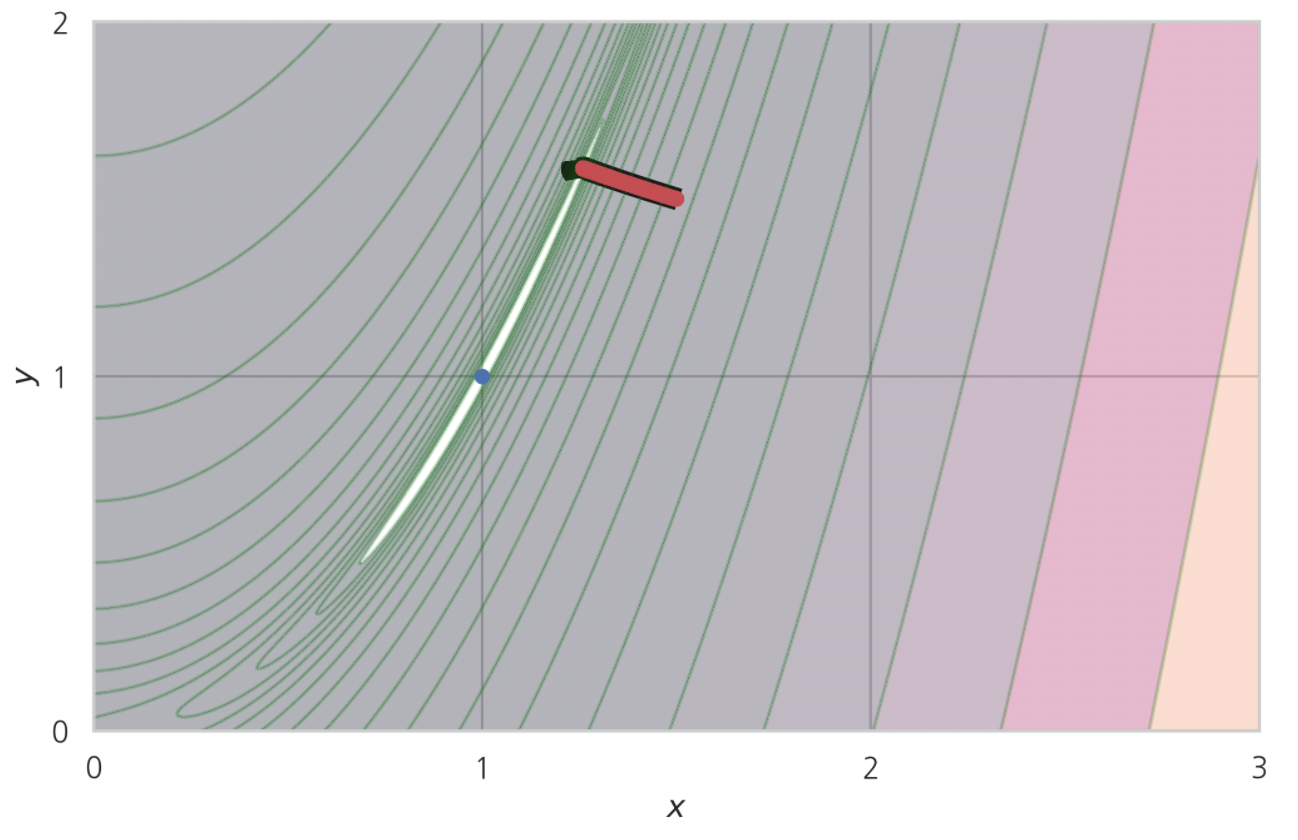
결론
따라서, 최대경사법 알고리듬에서는 적절한 크기의 스텝사이즈 설정이 매우 중요하다.
스텝사이즈 크기가 적절하지 못하면 오히려 최적화에 방해됬다.
최대경사법 단점 2 : 시작점 위치에 따라 최적화 결과가 크게 달라진다.
최대경사법 알고리듬은 최적화 시작점 위치에 따라 완전히 다른 최적화 결과를 가져올 수 있다.
때때로 이게 최적화 과정에서 비효율을 초래한다.
위 로젠브록 함수를 다시 보자.
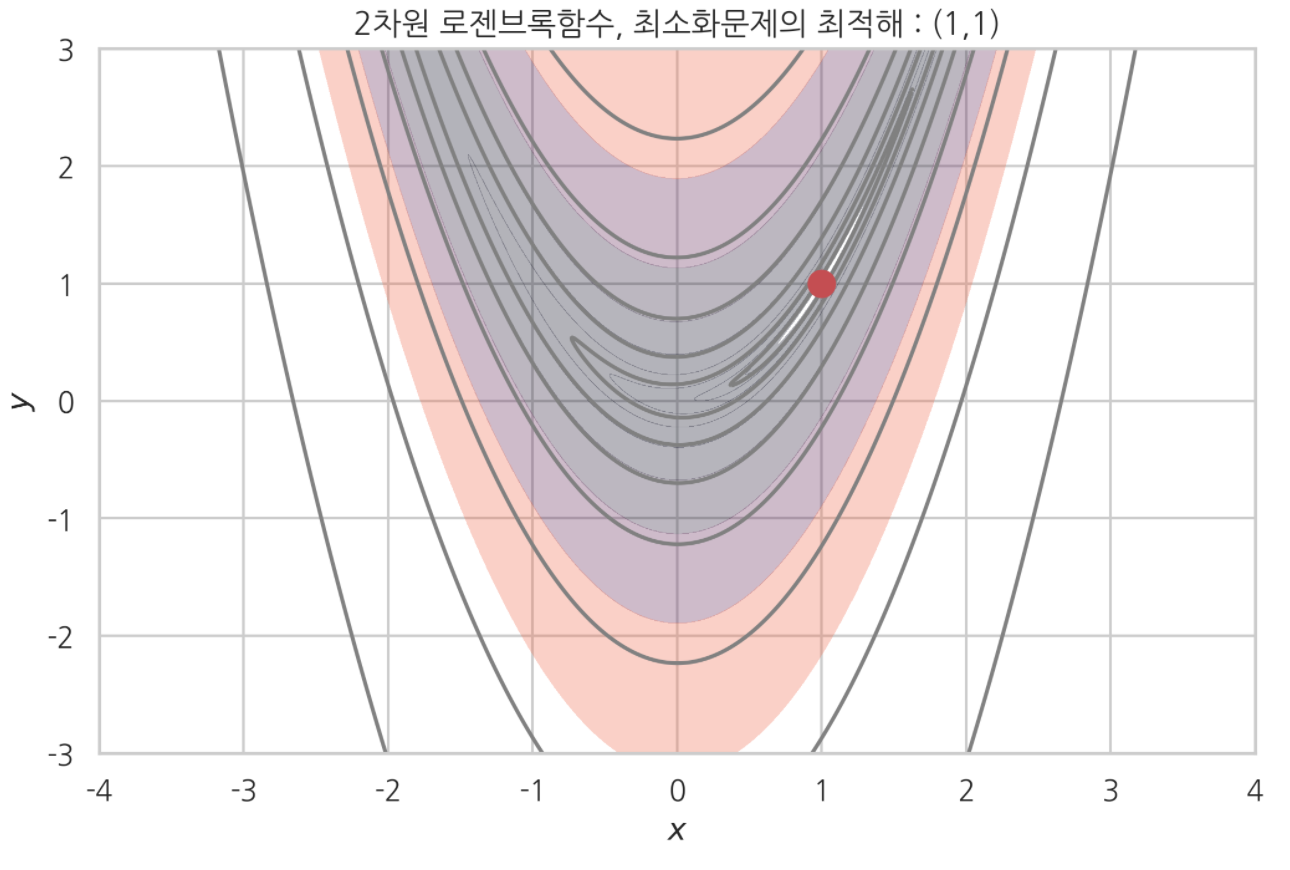
로젠브록함수는 $[1,1]$ 에서 최소점을 갖는다.
이 함수를 3차원 지형이라고 생각하면, 검은색 부분은 움푹 파인 골짜기에 해당한다.
그리고 최소점이 있는 $(0,2)$ 부터 $(2,0)$ 영역은 깊은 계곡과 같은 모양을 띄고 있다.
앞에서 로젠브록함수 최적화 할 때는 $[-1,-1]$ 에서 최적화를 시작했다.
계곡이 아닌 다른 어떤 지점에서 최적화 시작했다는 말이다.
그렇다면 최적화 시작점을 옮겨서, 최적점 근처 ‘계곡’에서 최적화를 시작하면 어떨까?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(0, 3, 500)
yy = np.linspace(0, 3, 500)
X,Y = np.meshgrid(xx, yy)
Z = rosenbrook(X,Y)
plt.contourf(X,Y,Z, alpha=0.3, levels=np.logspace(-1,4,20))
plt.contour(X,Y,Z, colors='green',levels=np.logspace(-1,4,20), alpha=0.2) # 로젠브록함수 계곡에 해당하는 지역
plt.plot(1,1, 'bo', markersize=5)
plt.xlim(0,3)
plt.ylim(0,2)
plt.xticks(np.linspace(0,3,4))
plt.yticks(np.linspace(0,2,3))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
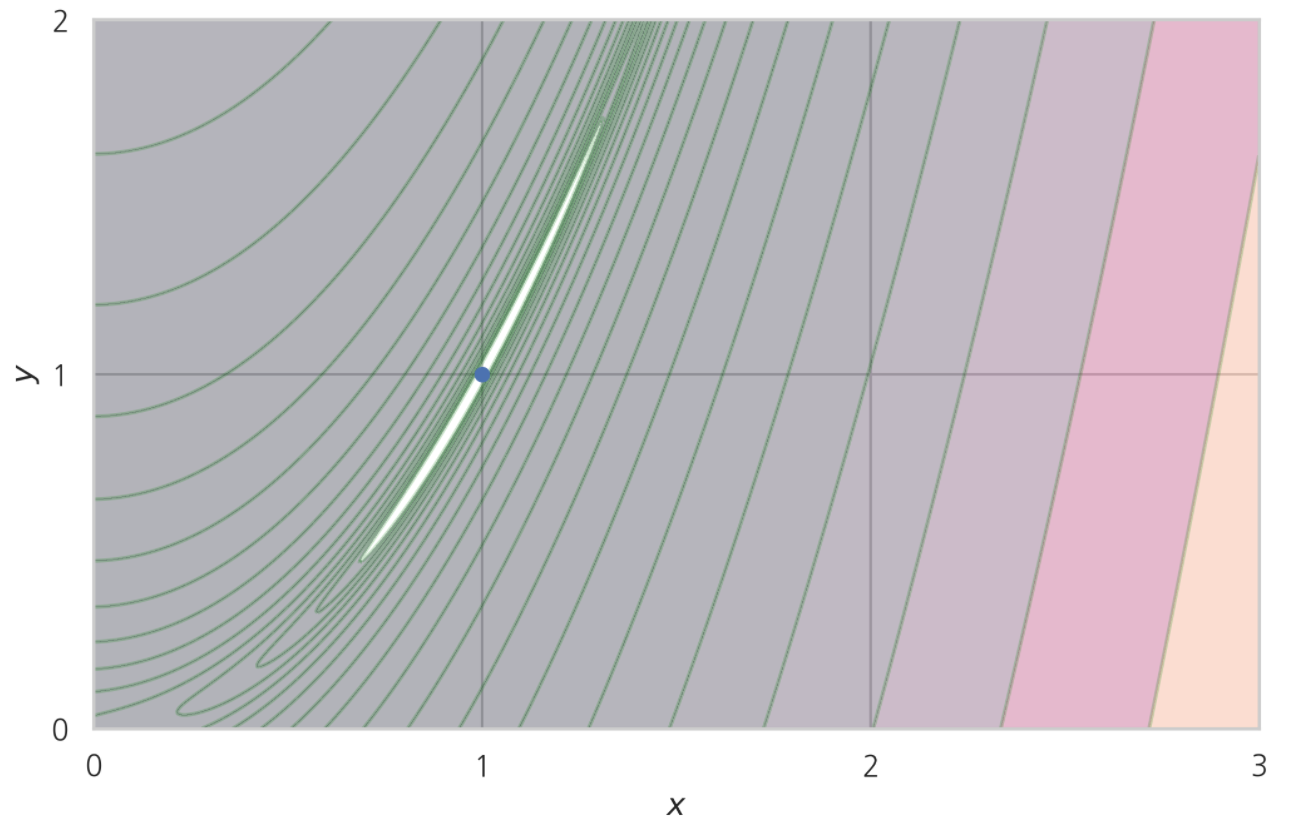
바로 여기 이 지역 말이다.
진동현상 발생
계곡의 $[1.5, 1.5]$ 점에서 최적화를 시작해봤다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(0, 3, 500)
yy = np.linspace(0, 3, 500)
X,Y = np.meshgrid(xx, yy)
Z = rosenbrook(X,Y)
plt.contourf(X,Y,Z, alpha=0.3, levels=np.logspace(-1,4,20))
plt.contour(X,Y,Z, colors='green',levels=np.logspace(-1,4,20), alpha=0.2) # 로젠브록함수 계곡에 해당하는 지역
mu = 1.8e-3 # 스텝사이즈
a = 1.5
b = 1.5
for i in range(10) :
plt.plot(a,b, 'ro', markersize=5)
plt.arrow(a, b, -0.95*mu*gradient(a, b)[0], -0.95*mu*gradient(a, b)[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw = 2)
next_step = np.array([a,b]) - mu*gradient(a,b)
a = next_step[0]
b = next_step[1]
plt.plot(1,1, 'bo', markersize=5)
plt.plot(a,b, 'ro', markersize=5)
plt.suptitle('최대경사법 이용한 2차원 함수 최적화 - 진동현상 발생하는 예', y=1.02)
plt.title('(1.5, 1.5) 에서 최적화 시작, 각 점 그레디언트벡터 반대방향으로 진동하듯 내려간다')
plt.xlim(0,3)
plt.ylim(0,2)
plt.xticks(np.linspace(0,3,4))
plt.yticks(np.linspace(0,2,3))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
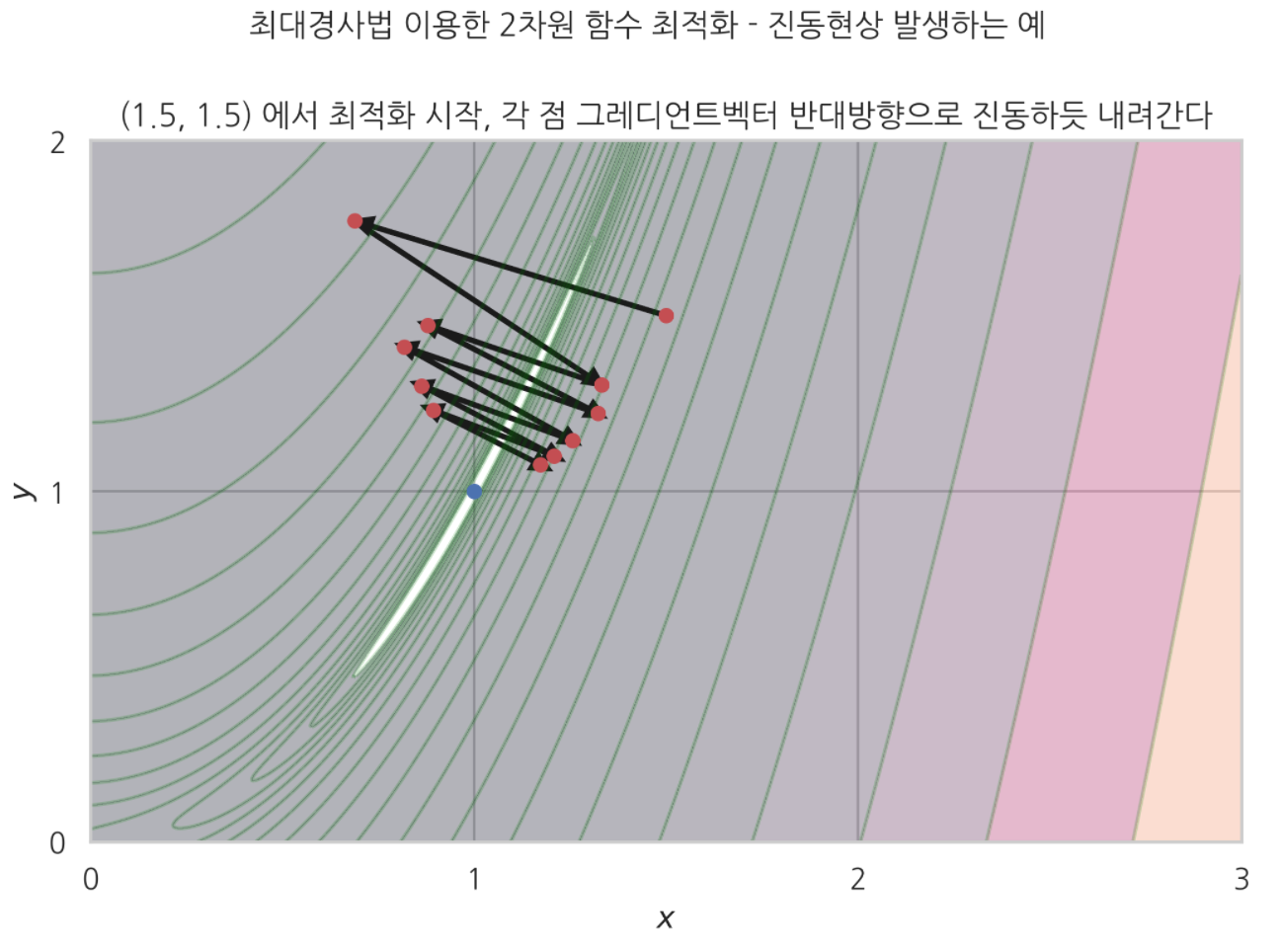
스텝사이즈 $1.8e-3$ 에서, $[1.5, 1.5]$ 에서 시작한 점이 그레디언트벡터 반대방향(기울기 가장 크게 감소하는 방향) 따라 좌우로 진동하듯 이동했다.
이런 현상을 ‘진동현상’ 이라고 한다.
보다시피, 진동현상이 발생하면 최적화 시간이 오래 걸리고, 최적화 효율성이 떨어지는 문제 발생한다.
진동현상 말고도
최대경사법에서, 최적화 시작점이 어디냐는 진동현상 말고도 완전히 다른 최적화 결과를 내놓을 수 있다.
아래는 앞에 기록했던 $[-1,-1]$ 에서 최적화를 시작한 예다.
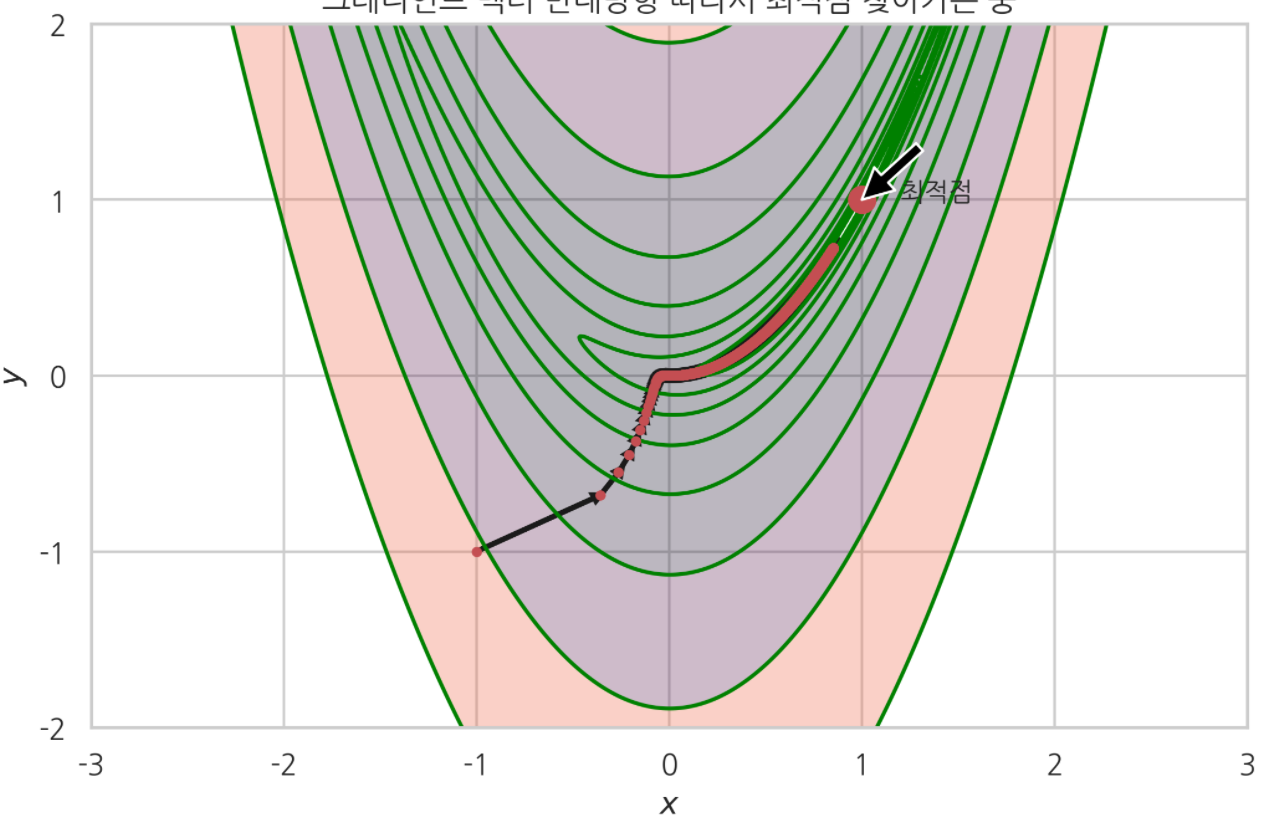
$[-1,-1]$ 에서 시작하면 위에 결과처럼 최적점을 찾아간다.
반면
다른 스텝 사이즈, 다른 시작 위치로 최적화 했을 때,
전혀 다른 최적화 결과를 관찰할 수 있었다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(-3,3,400)
yy = np.linspace(0,3.5,500)
X, Y = np.meshgrid(xx,yy)
Z = rosenbrook(X,Y)
levels=np.logspace(-1, 4, 10)
plt.contourf(X,Y,Z, levels=levels, alpha=0.3)
plt.contour(X,Y,Z, levels=levels, colors='g', alpha=0.2)
mu = 1.8e-3
a = 2
b = 2
for i in range(1000) :
plt.plot(a, b, 'ro', markersize=5)
n = np.array([a,b]) - mu*gradient(a,b)
n_ = -mu*gradient(a,b)
plt.arrow(a,b, 0.95*n_[0], 0.95*n_[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw=2)
a = n[0]
b = n[1]
plt.suptitle('로젠브록함수 최대경사법 최적화(최소화문제)', y=1.03)
plt.title('최적화 시작 위치 : $[2,2]$, 스텝사이즈 : 1.8e-3')
plt.show()
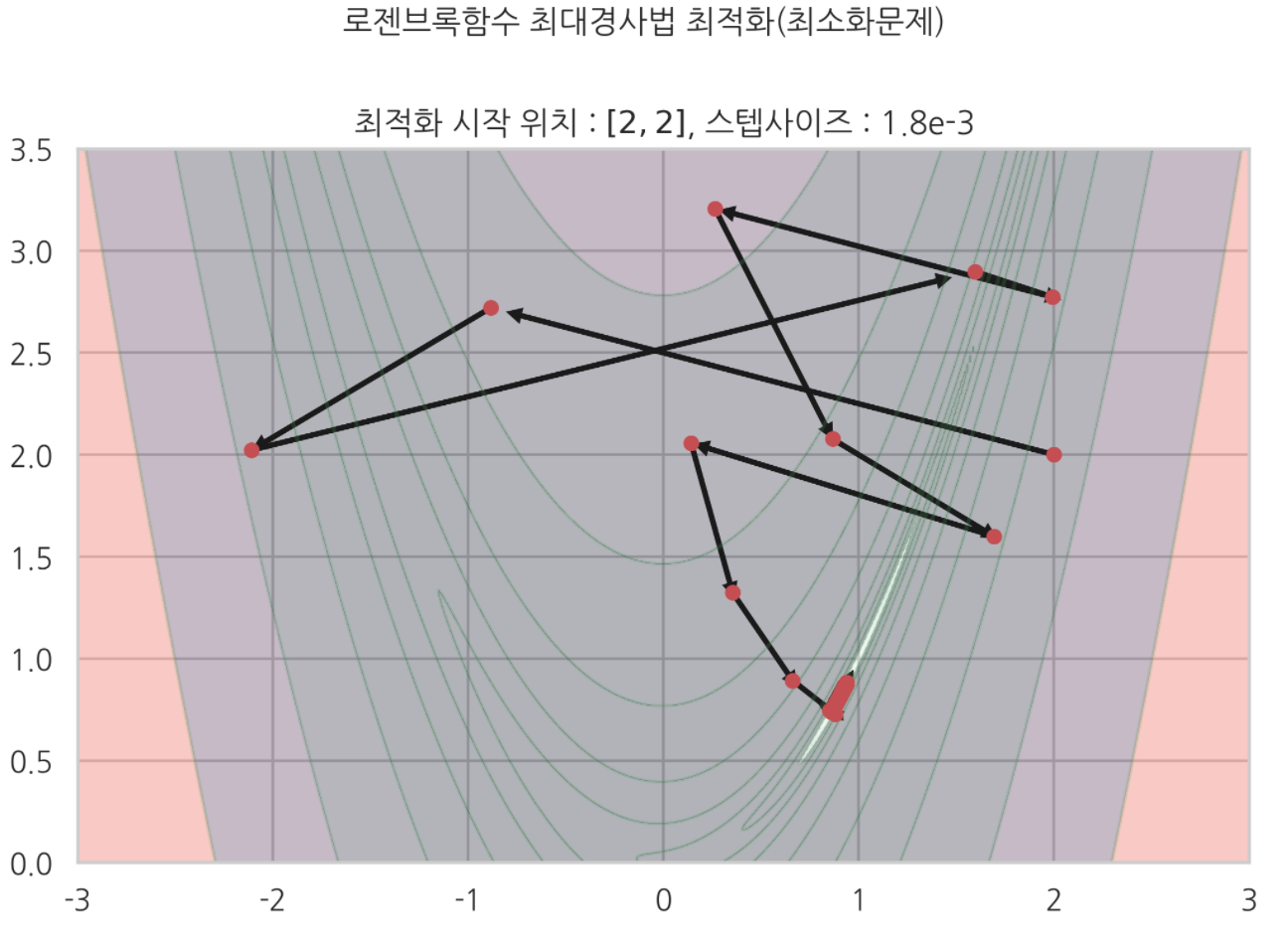
이처럼 최대경사법 알고리듬은
스텝사이즈가 얼마냐
최적화 시작 위치가 어디냐에 따라서
최적화 결과가 완전히 달리질 수 있다.
또 최적화 과정에서 큰 비효율이 초래되는 경우도 왕왕 발생했다.
뉴턴방법
정의 :
스텝사이즈 $\mu$ 대신 헤시안행렬의 역행렬을 사용하는,
개선된 최대경사법.
$x_{n+1} = x_{n}-H[f(x_{n})]^{-1}\nabla{f_{x_{n}}}$
헤시안행렬의 역행렬은 최적 스텝사이즈다.
$x_{n+1}-x_{n} = -H[f(x_{n})]^{-1}\nabla{f_{x_{n}}}$
특징 :
함수가 2차함수에 가까울 수록, 최적점에 빨리 수렴한다.
장점 :
$\mu$ 사용하는 최대경사법 대비 수렴 속도가 빠르고 효율적이다.
단점 :
- 2차도함수 행렬.헤시안행렬을 사람이 직접 구해야 하기 때문에 번거롭고 계산이 많다(귀찮다).
- 함수 형상이 2차함수와 비슷하지 않은 경우, 최적화가 잘 안 될 수 있다.
뉴턴방법 예시)
위에서 최대경사법으로 최적화 했던 로젠브록함수를 뉴턴방법 최적화 하고, 시각화했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(0, 3, 500)
yy = np.linspace(0, 3, 500)
X,Y = np.meshgrid(xx, yy)
Z = rosenbrook(X,Y)
plt.contourf(X,Y,Z, alpha=0.3, levels=np.logspace(-1,4,20))
plt.contour(X,Y,Z, colors='green',levels=np.logspace(-1,4,20), alpha=0.2) # 로젠브록함수 계곡에 해당하는 지역
def next_step(x,y) :
return np.array([x,y]) - H_INV(x,y)@gradient(x,y)
facecolor = ['black', 'green', 'blue', 'red']
a = 1.5
b = 1.5
for i in range(4) :
if i == 0 :
plt.plot(a,b, 'bo', markersize=5)
elif i == 3 :
plt.plot(a,b,'go', markersize=5)
else :
plt.plot(a,b, 'ro', markersize=5)
n = next_step(a,b)
adjusted_gradient = H_INV(a,b)@gradient(a,b)# 최적스텝사이즈 * 그레디언트벡터 = 변형된 그레디언트벡터
if i == 3 :
pass
else :
plt.arrow(a, b, -0.95*adjusted_gradient[0], -0.95*adjusted_gradient[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw=2)
a = n[0]
b = n[1]
plt.suptitle('뉴턴방법 : 함수형상이 2차함수에 가까울 수록 더 빨리 수렴한다', y=1.02)
plt.title('진동현상 없이 단 4번만에 최적점에 수렴')
plt.text(0.8, 1.08, '최적해')
plt.annotate('', xy=[1.6, 1.8], xytext=[1.8,1.8], arrowprops={'facecolor':'blue'})
plt.text(1.6, 1.6, '방향. 길이 조정된 그레디언트벡터(H*g)')
plt.xlim(0, 3)
plt.ylim(0,3)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def H(x,y) :
np.array([
[1200*x**2-400*y+2, -400*x],
[-400*x, 200]])
r = 80000*x**2-80000*y+400
result = (1/r)*np.array([[200, 400*x],[400*x, 1200*x**2-400*y+2]])
def H_INV(x,y) :
return (1/(80000*x**2-80000*y+400))*np.array([[200, 400*x],[400*x, 1200*x**2-400*y+2]])
def next_step(x,y) :
return np.array([x,y]) - H_INV(x,y)*gradient(x,y)
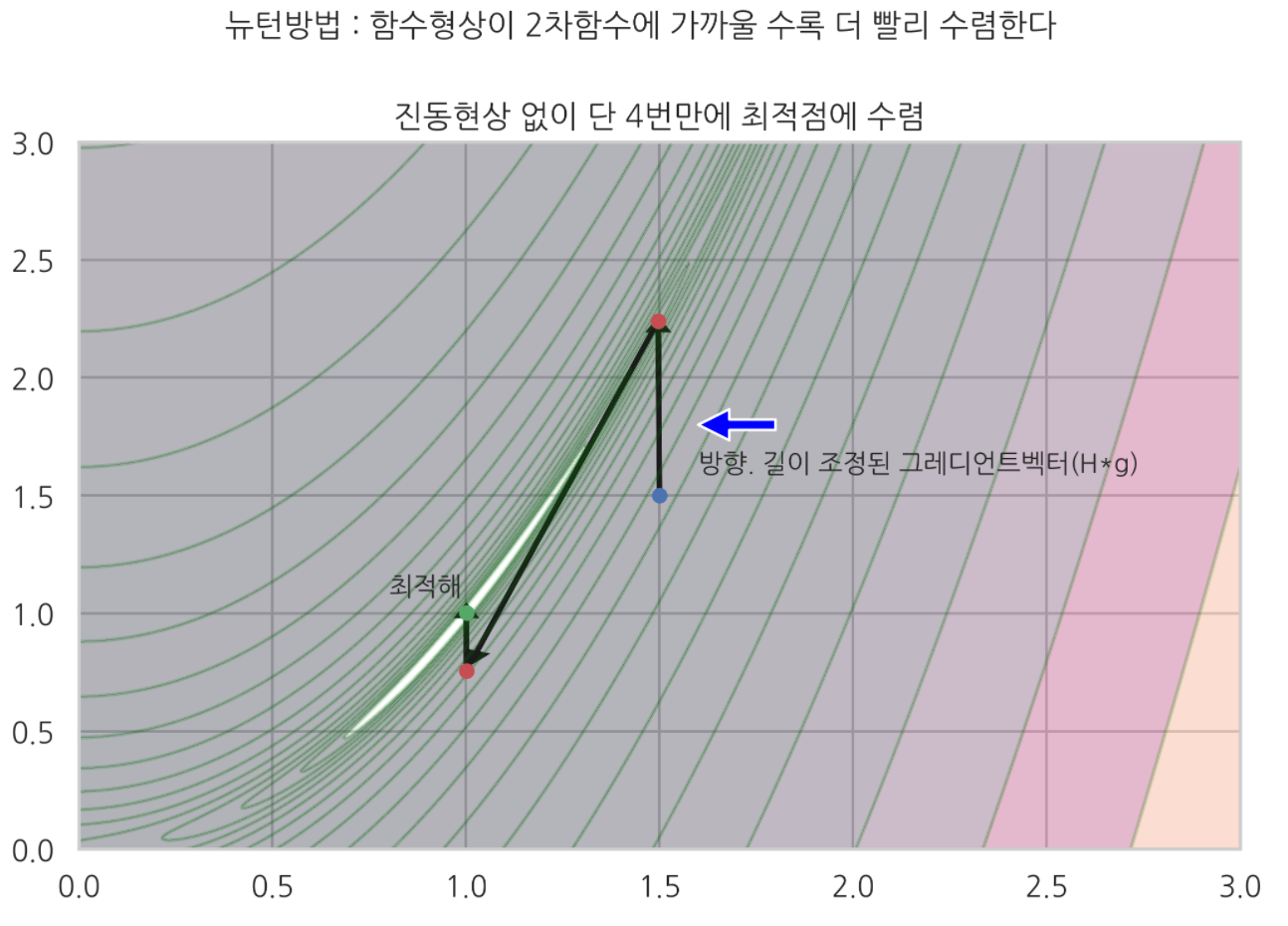
최대경사법은 계곡형상 지형에서, 진동현상 나타나는 걸 관찰할 수 있었다.
하지만 뉴턴방법은 거리. 방향이 변형된 그레디언트 벡터를 사용하기 때문에, 위 그림처럼 4번만에 최적해에 도달하는 걸 볼 수 있었다.
위 코드에는 기록하지 않았지만, 미분은 심파이 심볼릭연산을 사용했다.
다른 위치에서 시작하는 뉴턴방법 로젠브록함수 최적화)
최대경사법에서 아래와 같았던 최적화 결과가
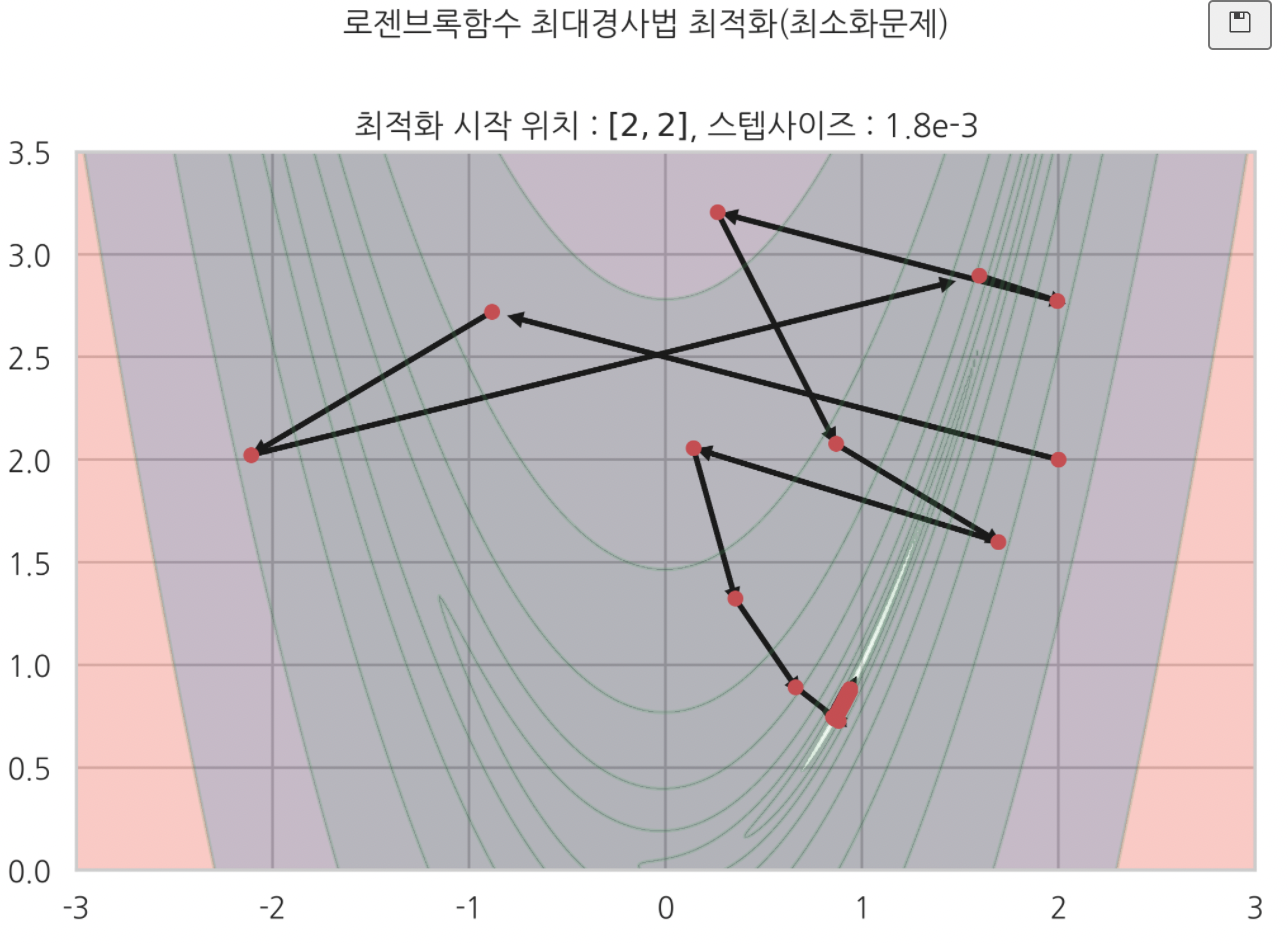
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(-5,5,400)
yy = np.linspace(-4,4,500)
X, Y = np.meshgrid(xx,yy)
Z = rosenbrook(X,Y)
levels=np.logspace(-1, 4, 10)
plt.contourf(X,Y,Z, levels=levels, alpha=0.3)
plt.contour(X,Y,Z, levels=levels, colors='g', alpha=0.2)
a = 2
b = 2
# 뉴턴방법(개선된 최대경사법)
for i in range(10) :
plt.plot(a,b, 'bo', markersize=5)
n = np.array([a,b]) - H_INV(a,b)@gradient(a,b)
n_ = - H_INV(a,b)@gradient(a,b)# 다음위치
plt.arrow(a,b, 0.95*n_[0], 0.95*n_[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw=2)
a = n[0]
b = n[1]
plt.suptitle('로젠브록함수 뉴턴방법 최적화(최소화문제)', y=1.03)
plt.title('같은 위치($[2,2]$)에서 단 4번만에 최적화 성공하는 걸 볼 수 있다')
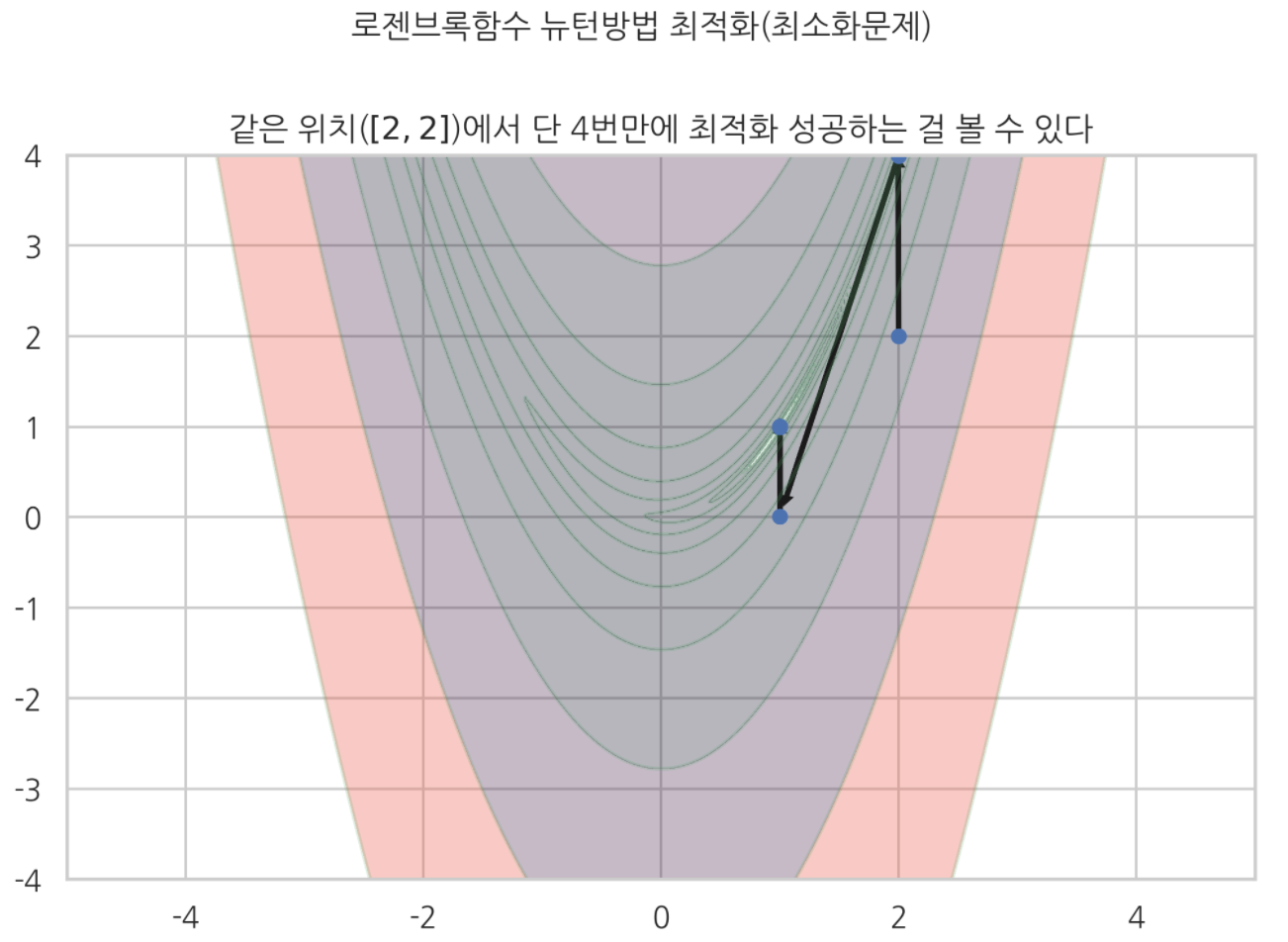
단 4번만에 깔끔하게 최적화 성공했다.
다른 시작점에서도
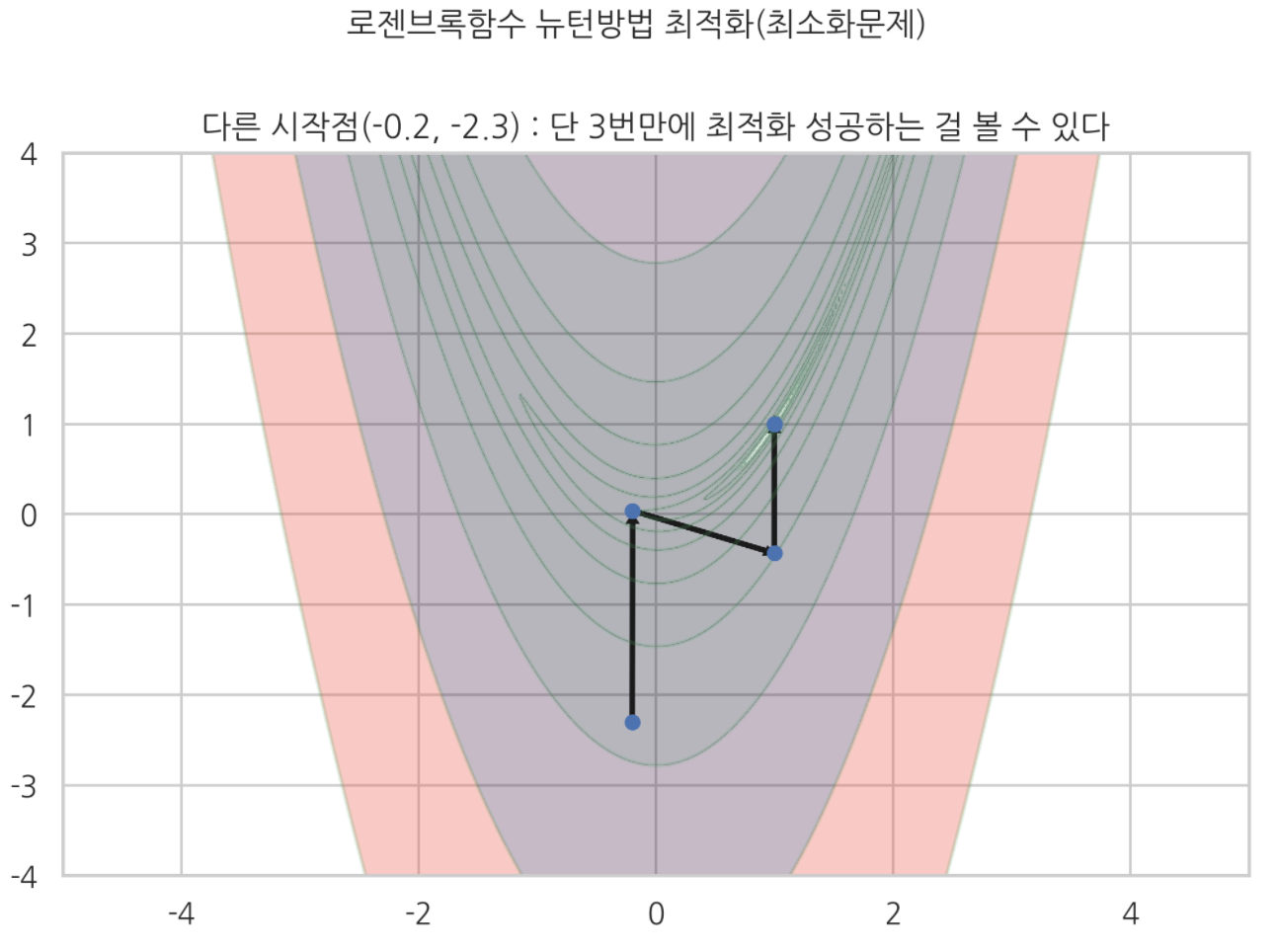
3번만에 최적화 성공했다.
하지만 같은 지점에서 $\mu$ 스텝사이즈를 사용하는 최대경사법으로는
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def rosenbrook(x,y) :
return (1-x)**2+100*(y-x**2)**2
def gradient(x,y) :
return np.array([-400*x*(-x**2+y)+2*x-2, -200*x**2+200*y])
xx = np.linspace(-3,3,400)
yy = np.linspace(-3,3.5,500)
X, Y = np.meshgrid(xx,yy)
Z = rosenbrook(X,Y)
levels=np.logspace(-1, 4, 10)
plt.contourf(X,Y,Z, levels=levels, alpha=0.3)
plt.contour(X,Y,Z, levels=levels, colors='g', alpha=0.2)
mu = 1.8e-3
a = -0.2
b = -2.3
for i in range(3) :
plt.plot(a, b, 'ro', markersize=5)
n = np.array([a,b]) - mu*gradient(a,b)
n_ = -mu*gradient(a,b)
plt.arrow(a,b, 0.95*n_[0], 0.95*n_[1], head_width=0.04, head_length=0.04, fc='k', ec='k', lw=2)
a = n[0]
b = n[1]
plt.plot(a,b, 'ro', markersize=5)
plt.suptitle('로젠브록함수 최대경사법 최적화(최소화문제)', y=1.03)
plt.title('3번 시도로는 최적화 할 수 없다')
plt.plot(1,1, 'bo', markersize=5)
plt.show()
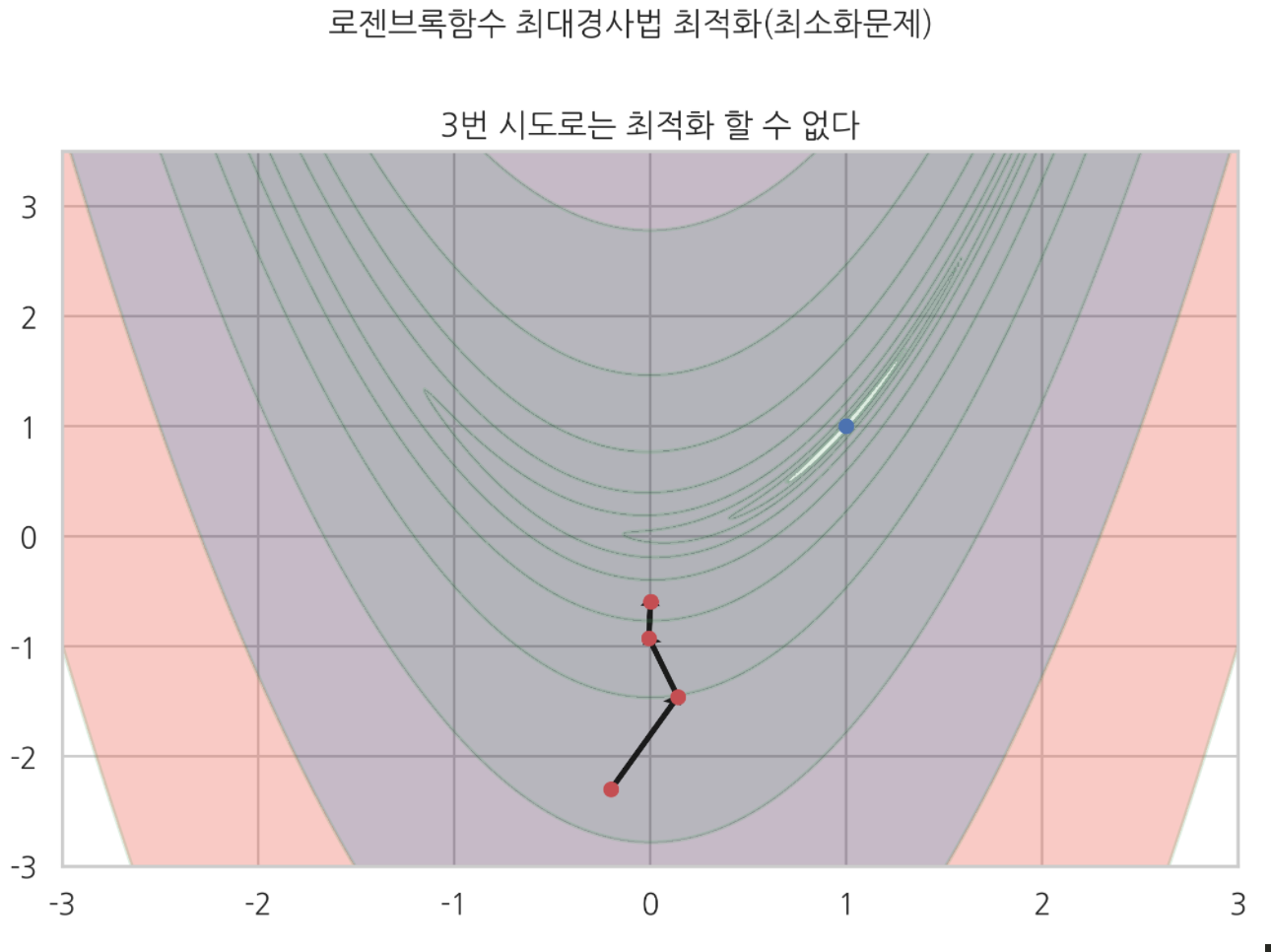
3번 시도로는 최적화 할 수 없었다.
준 뉴턴방법
정의 :
뉴턴방법이면서,
헤시안 행렬을 사람이 직접 계산하지 않아도 되는 최적화 방법.
헤시안 행렬을 알고리듬이 수치적으로 대략 계산해서 넣는다.
계산량이 많아졌던 헤시안 행렬 계산을 사람이 직접 안 해도 된다는 장점. 있다.
예 :
BFGS 방법
사이파이로 최적화 하기
디폴트 최적화 알고리듬은 준 뉴턴방법, BFGS 방법이다.
단변수함수
sp.optimize.minimize(f, x0, jac=)
- f : 최적화 할 함수 이름
- x0 : 최적화 시작 위치
- jac : 그레디언트 벡터
예)
1
2
3
4
def f(x) :
return (x-2)**2+2
x0 = 0 # 초깃값
sp.optimize.minimize(f, x0)
최적화에 성공할 경우. 다음과 같은 결과가 출력된다.
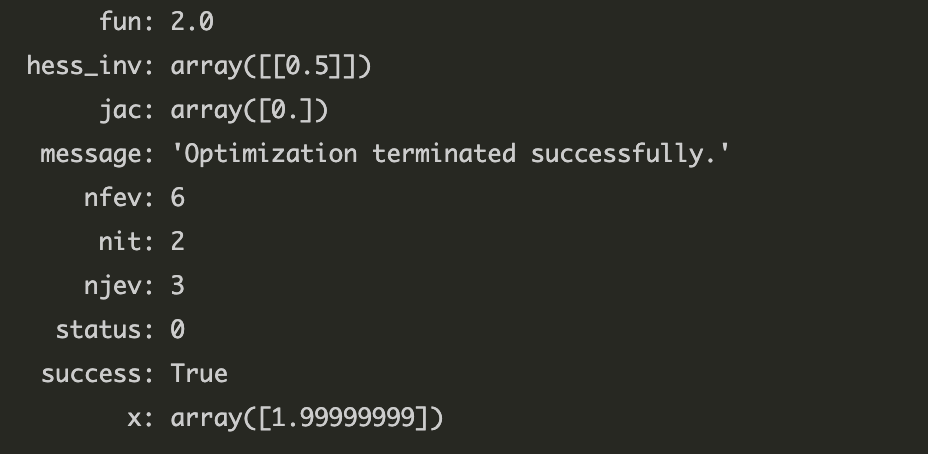
nfev 는 함수 호출 횟수를 의미한다.
한마디로, ‘얼마만에 최적화에 성공했냐’를 보여주는 것이다.
함수 호출 횟수를 줄이고, 최적화를 더 빨리 성공하기 위해서는
jac= 인수에 그레디언트 벡터를 직접 만들어서 넣어주면 된다.
그레디언트 벡터 함수 직접 넣어서 함수 호출 횟수 줄이는 경우
1
2
3
4
def g(x) :
return 2*x-4 # 그레디언트벡터 함수 (1차 도함수)
sp.optimize.minimize(f, x0, jac=g)
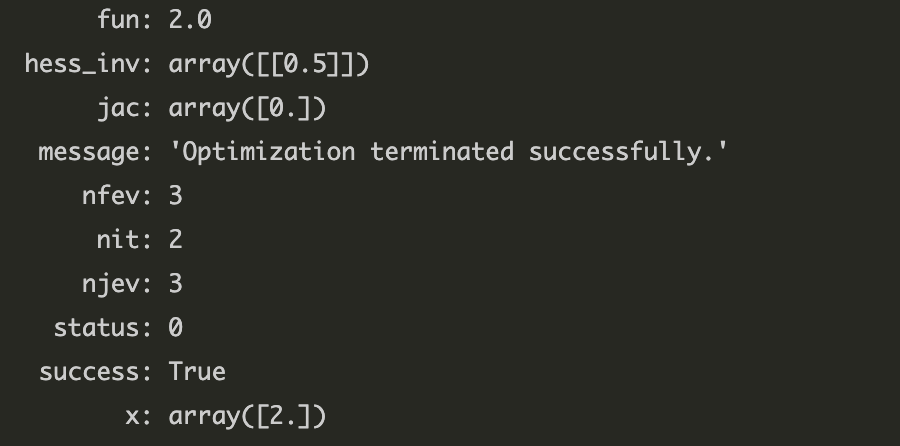
함수 호출 횟수가 6번에서 3번으로 줄어들었다.
다변수함수
다변수함수를 사이파이로 최적화 할 때는, 함수가 벡터 입력을 받을 수 있도록 바꿔야 한다.
1
2
3
4
5
6
def f(x) :
return (1-x[0])**2+100*(x[1]-x[0]**2)**2
x0 = (-1,1)
result = sp.optimize.minimize(f, x0)
result
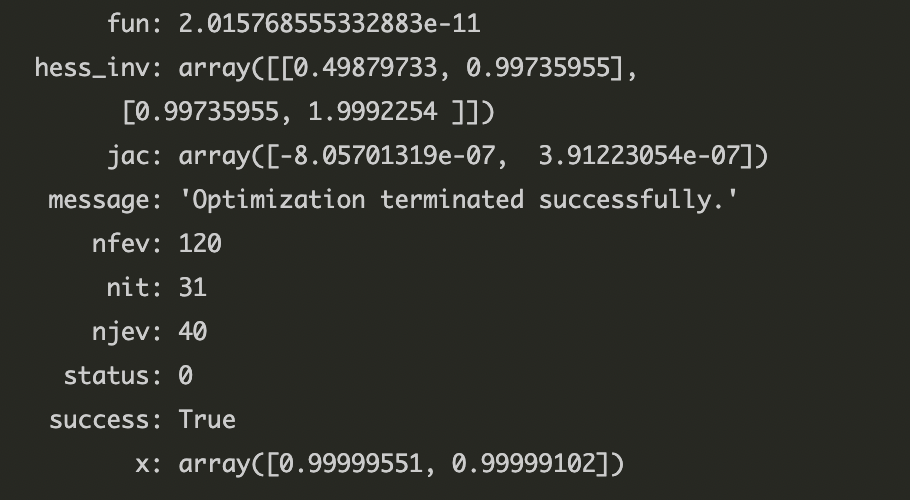
보면 f(x) 안에 벡터 x 입력을 받아 요소별로 인식할 수 있도록 $x[0], x[1]$ 형태로 바꿔놨다.
마찬가지로 그레디언트벡터 함수 넣어주면 계산 속도가 빨라진다.
1
2
3
4
5
6
7
8
9
10
# 그레디언트벡터 함수 삽입한 결과
def f(x) :
return (1-x[0])**2+100*(x[1]-x[0]**2)**2
def gradient(x) :
return np.array([-400*x[0]*(-x[0]**2+x[1]) + 2*x[0]-2, -200*x[0]**2+200*x[1]])
x0 = (-1,1)
result = sp.optimize.minimize(f, x0, jac=gradient)
result
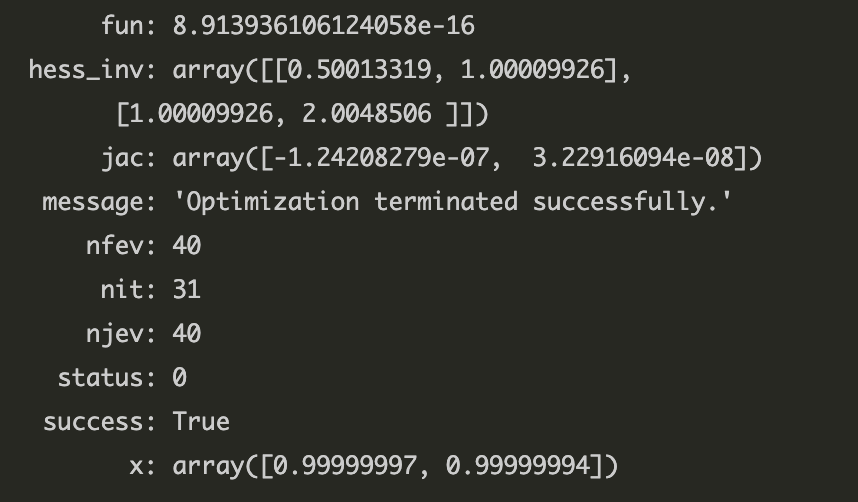
함수 호출 횟수가 120회에서 40회로 줄어들었다.
