‘프로그래머가 알아야 할 알고리즘 40’(임란 아마드 지음, 길벗 출판사) 을 통해 페이지랭크 알고리듬, 선형계획법 알고리듬을 공부. 복습하고나서, 그 내용을 내 언어로 바꾸어 기록한다.
페이지랭크(PageRank) 알고리듬
정의
다른 웹페이지로 부터 받은 링크 수에 따라, 웹페이지 별 중요도 매기는 알고리듬.
근간 아이디어
“다른 웹페이지로부터 링크 많이 받을 수록, 중요한 페이지다”
문제 기능적 요구사항
입력: 웹페이지 간 연결 나타낸 그래프(인접행렬)
출력: 페이지 별 가중치(중요도)
여기서는 각 페이지 가중치 계산 및 출력까지 안 가고, 인접행렬 이용해서 전이행렬 계산(출력) 하는 것 까지만 알고리즘 구현했다.
구현
웹페이지 간 연결 상태 표현한 그래프
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 웹페이지 간 연결 그래프
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
myweb = nx.DiGraph()
mypages = range(1,6) # 1~5번 페이지
# 페이지 간 연결상태
connections = [(1,3), (2,1), (2,3), (3,1), (3,2), (3,4), (4,5), (5,1), (5,1), (5,4)]
myweb.add_nodes_from(mypages) # 그래프에 노드 5개 추가
myweb.add_edges_from(connections) # 각 노드 사이 간선 추가
pos = nx.shell_layout(myweb)
nx.draw(myweb, pos, arrows=True, with_labels= True)
plt.title('sample graph(network)')
plt.show()
시각적으로 표현한 웹페이지 간 연결상태
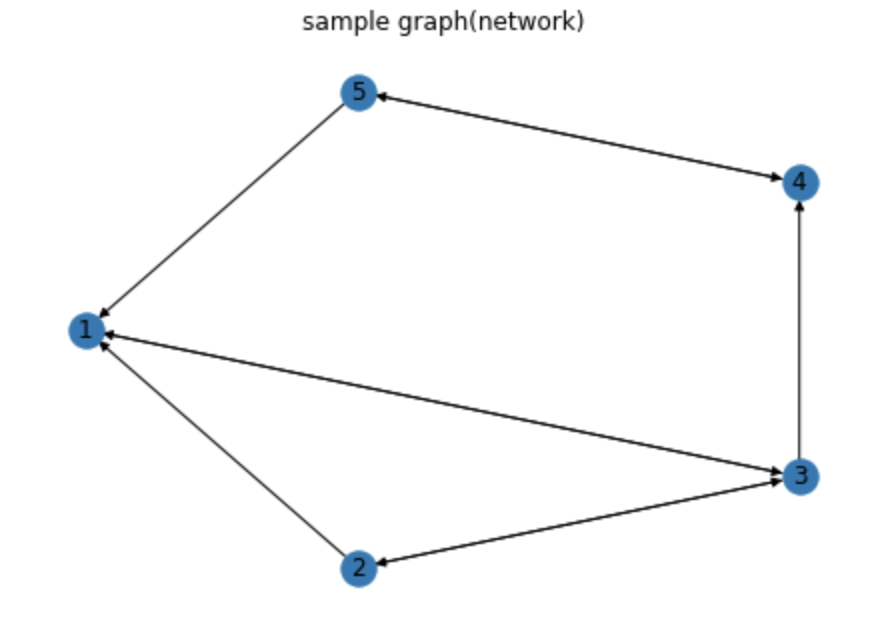
페이지랭크 알고리듬
- 입력: 그래프(인접행렬)
- 출력: 전이행렬
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 페이지랭크 알고리듬 구현
def pagerank_algorithm(agraph) :
m = nx.to_numpy_matrix(agraph)# 그래프를 인접행렬로 변환
sum = np.squeeze(np.asarray(np.sum(m, axis=1)))
prob_sum = np.array([1.0/x if x > 0 else 0 for x in sum])
G = np.asarray(np.multiply(m.T, prob_sum))
p = np.ones(len(agraph))/len(agraph)
return G,p
# 결과물 출력
pagerank_algorithm(myweb)
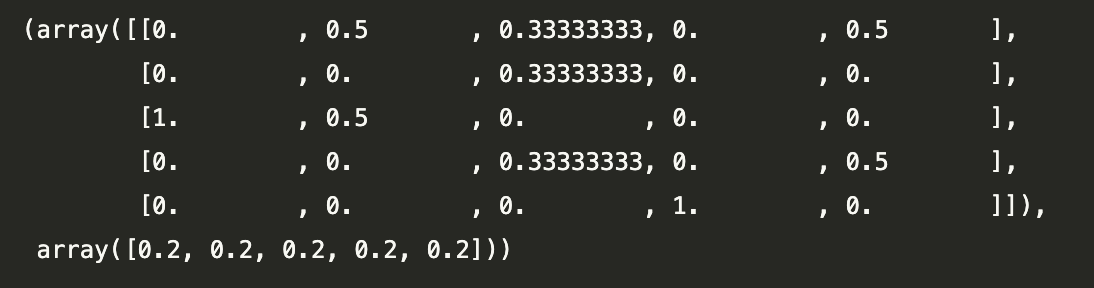
첫번째 array 가 알고리듬 출력인 전이행렬이다.
각 열이 각각 1,2,3,4,5 번 웹페이지를 나타내고, 열마다 각 값은 그 열에 해당하는 웹페이지가 다른 웹페이지로 연결될 확률 나타낸다.
예컨대 3번 열은 1,2,4 번 3개 웹페이지와 연결되어 있기 때문에, 각 값이 0.33333 으로 나온 것이다.
선형 계획법(Linear programming; LP문제)
정의
선형함수에 대해, 부등식/등식 제한조건 걸고 최적화 하는 알고리듬.
책 예제
목적함수에서 사용하는 변수 : $x, y$ (각 로봇 생산량 의미한다)
목적함수 : $f(x,y) = 5000x + 2500y$
제약조건 :
- $x \ge 0$ (로봇 A 생산량은 0이거나 0보다 큰 양의 정수)
- $y \ge 0$ (로봇 B 생산량은 0이거나 0보다 큰 양의 정수)
- $3x+2y \leq 20$
- $4x+3y \leq 30$
- $4x+3y \leq 44$
이 책에서는 pulp 라이브러리 이용해서 선형 목적함수 최대화 하는 최적 입력 $x, y$ 찾았다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 선형 목적함수 부등식 제약조건 최적화 하기
import pulp
# 문제 정의
problem = pulp.LpProblem('Profit_maximizing_problem', pulp.LpMaximize)
# 문제에서 쓸 변수 정의
x = pulp.LpVariable('x', lowBound = 0, cat='Integer')
y = pulp.LpVariable('y', lowBound = 0, cat='Integer')
# 목적함수 정의
problem += 5000*x + 2500*y
# 부등식 제약조건 정의
problem += 3*x + 2*y <= 20
problem += 4*x + 3*y <= 30
problem += 4*x + 3*y <= 44
# 성능함수 최적해 계산
problem.solve() # 1 = True
1 (최적해 계산에 성공했다)
1
2
3
4
5
6
7
8
9
# 최적화 결과 확인
print(pulp.LpStatus[problem.status]) # 최적값 찾았다.
# x, y 최적해 출력
print(x.varValue);print(y.varValue) # x = 6, y = 1 최적해.
# 최적해 에서 목적함수 최대화된 값(maximized value)
# = 목적함수에 최적해 집어넣은 출력값
print(pulp.value(problem.objective))
Optimal
6.0
1.0
32500.0
