상관관계
상관관계 정의
확률변수-확률변수 간
- 한 확률변숫값을 알면 다른 확률변숫값에 대한 정보 얻을 수 있는 관계
- 또는 두 확률변수가 서로 영향 주고받는 관계
상관관계 종류
- 선형 상관관계
- 비선형 상관관계
표본 공분산
- 정의 : 확률변수 벡터(표본)들이 축에서 평균적으로 떨어진 정도
- 전제 : ‘축’ = 확률변수 각 표본값들의 평균 $(\bar{X}, \bar{Y})$
피어슨 상관계수
- 정의 : 두 확률변수 사이 선형상관 정도를 나타낸다.
$p = 1$ 이면 ‘완전 선형 상관관계’
$p = 0$ 이면 ‘무상관’ (선형 상관관계 없음)
$p = -1$ 이면 ‘완전 선형 반상관관계’
피어슨 상관계수 부호는 다변수 확률변수 표본 벡터 분포 방향을 알려준다
- 음수 : 오른쪽 아래
- 양수 : 오른쪽 위
피어슨 상관계수 절댓값 크기는 분포 기울기와는 아무 상관 없다 (얼마나 선형에 가까운지만 나타낸다)
피어슨 상관계수 한계
- 두 확률변수 사이 비선형 상관관계 있는 경우, 피어슨 상관계수값 적용 할 수 없다.
- 피어슨 상관계수만으로 벡터 분포 형상 완벽하게 추측하기엔 한계가 있다.
앤스콤 데이터셋에서 볼 수 있듯, 단 하나의 아웃라이어 데이터가 피어슨 상관계수값에 독보적 영향을 미칠 수 있다.
결과적으로 전체 분포가 선형 형상임에도, 피어슨 상관계수값은 1 또는 -1 안 나오는 경우가 생긴다.

다변수 확률변수의 표본공분산
- 다변수 확률변수는 단변수 확률변수 여러 개를 말한다.
또는 단변수 확률변수 모아놓은 벡터라고 봐도 된다.
- 다변수 확률변수 표본 공분산은 여러 개 단변수 확률변수의 표본들 간 공분산 구하는 것과 같다.
예를 들어 $X = [X1, X2, X3, X4]$ 인 경우 ($X$ 가 다변수 확률변수다)
$X1$ 의 표본과 $X2$ 의 표본 간 공분산 구하고, $X1$ 의 표본과 $X3$ 표본 간 공분산 구하고…
모든 단변수 확률변수 조합의 표본공분산 구하고, 표본공분산 행렬로 나타내면 된다.
- 다변수 확률변수의 이론적 공분산 행렬로 같은 개념에 기반해 구하면 된다.
예) $X1$ 과 $X2$ 모든 표본 간 공분산, $X1$ 과 $X3$ 모든 표본 간 공분산…
조건부 기댓값
- 조건부 기댓값 : 기댓값 구할 때, 원래 확률질량함수를 가중치로 써서 구했다.
조건부 기댓값은 확률질량함수 대신, 조건부확률질량(밀도)함수를 가중치로 써서 구한다.

- 조건부 기댓값은 예측문제의 답이 된다.
- $\hat{y}$ 으로 쓰기도 한다.
조건부 기댓값의 성질
- 상수에 대한 조건부 기댓값은 상수
- 일반적인 기댓값 성질 그대로 모두 만족한다
전체 기댓값의 법칙

- 조건부 기댓값의 기댓값은 $Y$ 확률변수 기댓값과 같다
조건부 분산
- 예측문제에서, 예측으로 못 맞추는 범위. 예측의 불확실성 의미한다.

조건부 편차 제곱의 조건부 기댓값.
- 내가 제시하는 예측 답은 조건부 확률분포 기댓값이다.
- 조건부 분산은 y값들이 이 기댓값에서 떨어져 있는 정도를 의미한다.
- 기댓값에서 떨어져 있는 y값들은 기댓값으로는 못 맞추는 값이다.
- [분산 크기 = 내가 기댓값으로 못 맞추는 범위]
따라서
- 조건부 분산이 크다 : 예측 불확실성이 높다 (못 맞추는 범위가 넓다)
- 조건부 분산이 작다 : 예측 불확실성이 작다 (못 맞추는 범위가 좁다)
전체 분산의 법칙
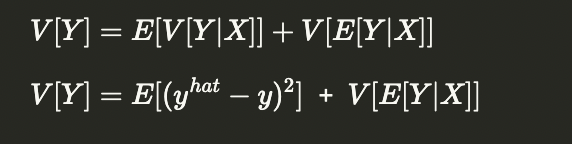
- 전체 분산의 법칙 식에서 편향-분산 상충법칙이 발생한다.
편향_분산 상충법칙
- 편향(예측오차)를 낮춰서 주어진 데이터에서 정답을 잘 맞추게 하면 모델이 복잡해지고, 자칫 과적합(오버핏팅) 문제가 발생할 수 있다.
오버핏팅이란 과적합 이라고도 하고, 주어진 데이터 내에서 정답은 매우 잘 맞추지만, 다른 데이터를 넣으면 예측 모델이 형편없이 못 맞추는 현상을 말한다.
즉 예측모델이 주어진 데이터는 과할 정도로 학습해서 거의 ‘외워 버렸지만’, 새 데이터는 형편없이 못 맞추는 것이다.
- 과최적화를 피하기 위해 모델을 단순하게 만들면, 분산(예측값 변동 정도)는 떨어지지만 이제 예측오차(틀렸을 때 얼마나 빗나가는가) 가 커진다.
이 같은 상충 현상을 ‘편향_분산 상충법칙’이라고 한다.
