회귀분석(Regression Analysis)
통계적 모형 중 회귀함수를 찾는 분석이다.
통계적(확률론적) 모형
입력과 출력 사이 관계가 일정하게 대응되지 않는 모형. 항상 오차를 수반한다.
$Y = f(x_{1}, x_{2}, x_{3}, … x_{n}) + \epsilon$
$\epsilon$ 이 오차항이며, $N(0, \sigma^{2})$ 을 따르는 확률변숫값이다. 따라서 출력 $Y$ 도 확률변숫값이다.
수학적(결정론적) 모형
입력과 출력 사이 일정한 대응관계 성립하는 모형. 수학적 함수다. 오차를 수반하지 않는다.
$Y = f(x_{1}, x_{2}, x_{3}, … x_{n})$
회귀모형은 통계적 모형이다.
회귀모형(Regression Model)
회귀모형은 회귀함수 $f(x_{i})$ 와 오차항 $\epsilon$ 으로 구성된다.
$Y = f(x_{1}, x_{2}, x_{3}, … x_{n}) + \epsilon$
회귀분석은 위 모형에서 회귀함수 $f(x_{1}, x_{2}, x_{3}, … x_{n})$ 를 찾는 분석이다.
- $Y:$ 반응변수, 종속변수
- $x_{1}, x_{2}, … x_{n}:$ 설명변수, 독립변수
- $\epsilon:$ 오차항
- $f(x_{1}, x_{2}, x_{3}, … x_{n}):$ 회귀함수
회귀모형 종류
회귀모형 = 회귀함수 + 오차
회귀함수 종류에 따라 회귀모형을 구분한다.
모수회귀모형
정의: 회귀함수 형태가 고정된 회귀모형
- 회귀분석 할 때는 형태 고정된 어떤 회귀함수로 모회귀모형을 설정하고, 그 모회귀모형의 추정모형(적합모형) 을 찾는다.
모수회귀모형 종류
- 단순선형회귀모형: $f(X) = \beta_{0}+\beta_{1}X$. 회귀함수가 1차원 선형함수다.
- 다중선형회귀모형: $f(X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}…+\beta_{n}X_{n}$. 회귀함수가 회귀계수와 설명변수 벡터의 선형조합 형태다.
- 비선형회귀모형: $f(X) = \frac{\beta_{0}X}{\beta_{1}+X}$. 회귀함수는 $\beta$ 와 설명변수 $X$의 비선형결합 형태다.
- $k-$차 다항회귀모형: $f(X) = \beta_{0}+\beta_{1}X + \beta_{2}X^{2}+\beta_{3}X^{3}…+\beta_{k}X^{k}$. 회귀함수가 회귀계수와 설명변수 $X$ $k$차 항의 선형조합 형태다.
- 로지스틱 회귀모형: 반응변수 $Y$ 가 이항분포(n번 중 성공 횟수)를 따를 때
- 로그선형모형: 반응변수 $Y$가 포아송분포를 따를 때
비모수회귀모형
정의: 회귀함수 $f(X)$ 형태가 고정되어 있지 않은 회귀모형
- 회귀함수는 특정 가정만 만족하면 된다. 예) 3번 미분 가능한 함수
회귀분석의 논리 흐름
아래와 같이 실현된 데이터를 내가 갖고 있다고 가정해보자.
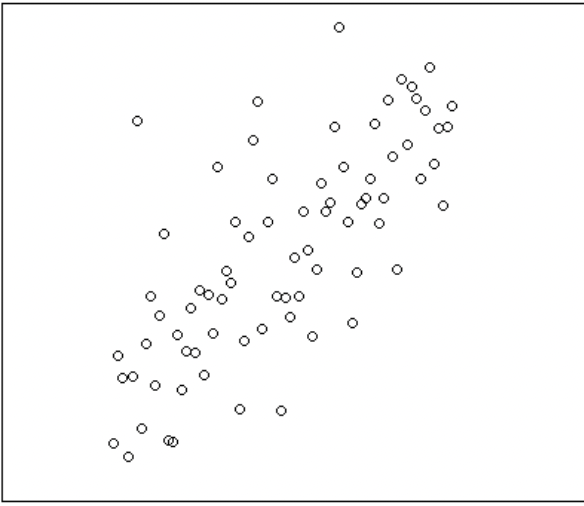
이 데이터는 본래 어떤 형태 모형에서 실현되었을까? 알 수 없다. 데이터를 실현시킨 본래 ‘참모형(True model)’ 을 아는 건 신의 영역이다. 인간은 알 수 없다.
$\Rightarrow$ 데이터를 발생시킨 본래 모형을 ‘참모형(True model)’ 이라고 한다.
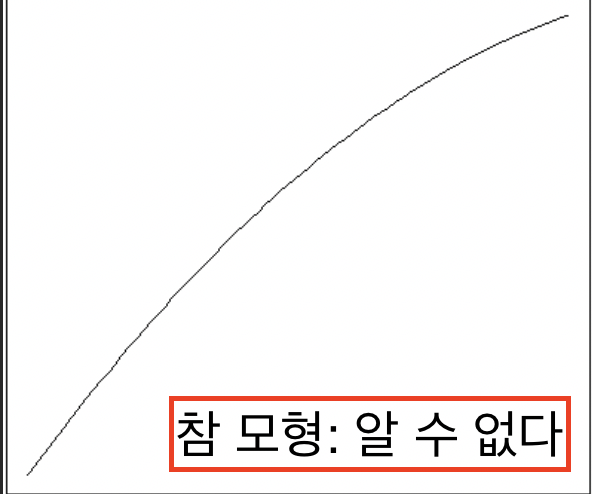
따라서 참 모형을 알아내는 건 우리 관심사가 아니다. 무슨 노력을 해도 알 수 없다. 미지의 영역이고, 신의 영역이다.
따라서 우리 인간은 참 모형의 대안으로, 실현된 데이터를 가장 잘 설명해 줄 수 있을 것 같은 임의의 모형을 ‘설정’ 한다. 이 모형을 ‘설정모형’ 이라고 한다.
위 산점도를 보니 데이터가 양의 선형 상관관계 있어 보인다. 데이터가 선형으로, 오른쪽 위를 향하고 있으므로 오른쪽 위를 향하는 ‘직선’으로 이 데이터를 잘 설명할 수 있을 걸로 보인다.
직선 형태 회귀함수 갖는 회귀모형은 단순선형회귀모형이 있다. 단순선형회귀모형을 설정모형으로 선택한다.
$\Rightarrow$ 설정모형: $Y = \beta_{0}+\beta_{1}X + \epsilon$
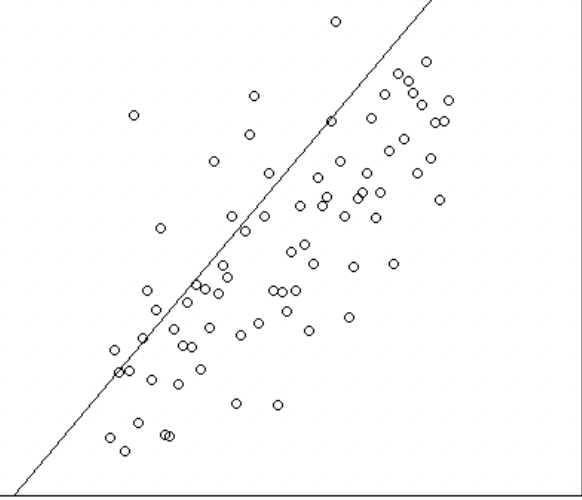
이 설정모형의 회귀함수 $Y =\beta_{0}+\beta_{1}X$는 $Y \vert{X}$ 분포의 기댓값들을 연결한 것과 같다. 이 회귀함수를 모회귀함수(모회귀선) 라고 한다.
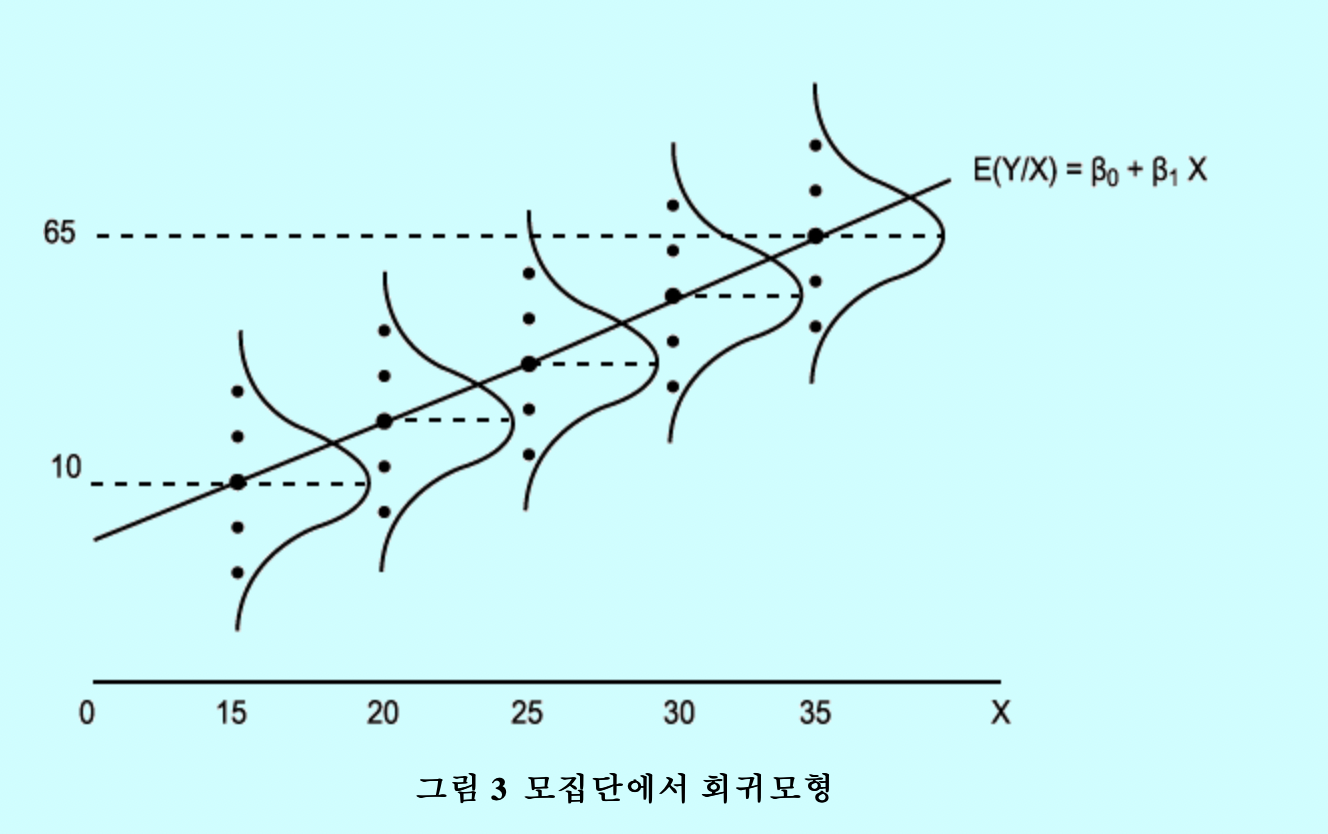
[이미지 출처: http://www.aistudy.com/math/regression_lee.htm ]
하지만 $Y \vert{X}$ 분포 기댓값들은 인간이 알 수 없는 미지의 값이다. 즉, 모회귀선은 알 수 없는 어떤 모수라고 생각할 수 있다. 미지의 모수를 추정하려면 실현된 데이터를 이용해서 추정치를 찾는다. 여기서도 마찬가지로, 실현된 데이터를 이용해서 모회귀선의 추정치를 찾는다.
회귀선과 실현된 데이터 사이 차이를 ‘잔차’라고 하는데, 이 잔차 제곱합(총 잔차 크기)이 최소가 되는 회귀선을 모회귀선 추정치로 삼는다.
$\Rightarrow$ 이 추정치를 ‘표본회귀선’ 이라 부른다. 표본회귀선은 $Y \vert{X}$ 분포 기댓값 추정치를 연결한 선이다. 한편 정규분포 기댓값 모수는 하나인데 기댓값 모수 추정치(표본평균)은 표본 얻을 때 마다 달라지는 것 처럼, 표본회귀선도 표본 얻을 때 마다 달라진다. 곧, 1개 표본회귀선은 모회귀선에 대한 여러 추정치중 하나에 불과하다.
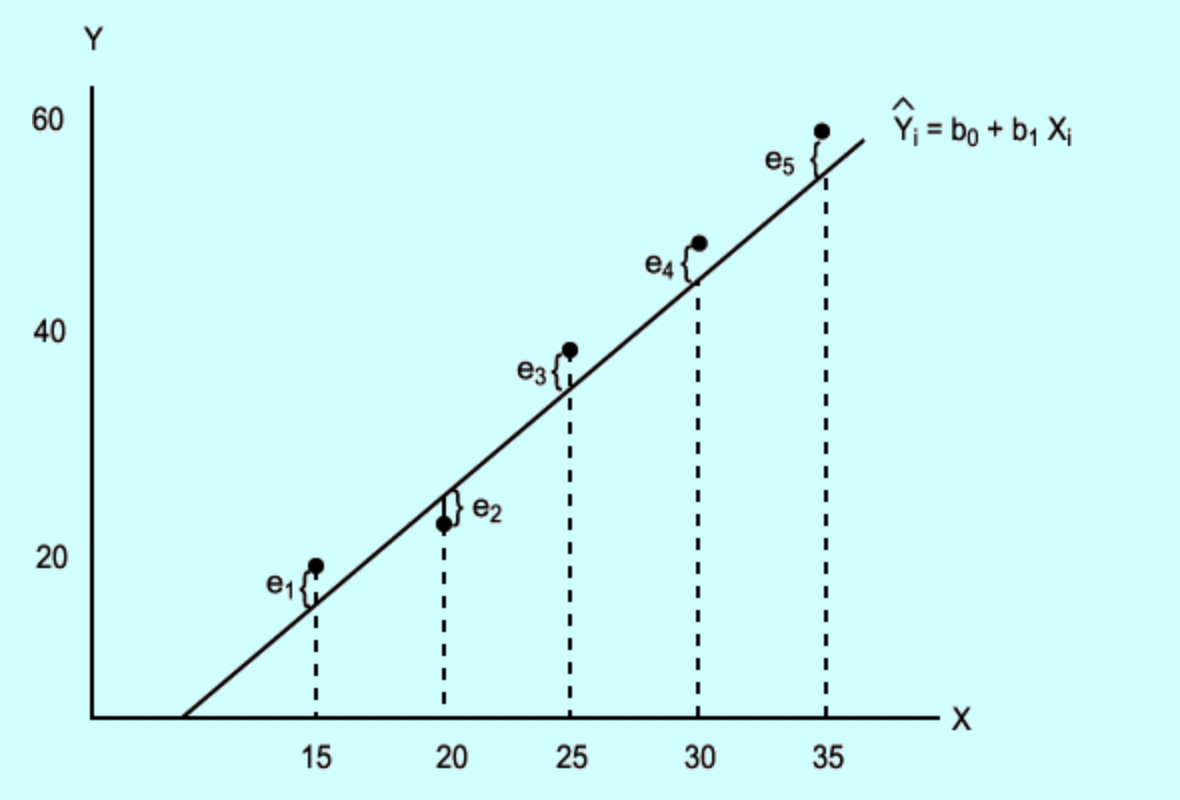
[이미지 출처: http://www.aistudy.com/math/regression_lee.htm ]
표본회귀선을 회귀함수로 삼은 회귀모형을 표본회귀함수 또는 적합모형(fitted model) 이라고 한다.
적합모형 = 표본회귀선(회귀함수) + $\epsilon$
적합모형은 모회귀모형 또는 설정모형에 대한 추정모형이다.
회귀분석의 최종목표는 주어진 데이터에 대해 적합모형의 회귀함수. 표본회귀선을 찾는 것이다.
모수회귀모형 - 단순선형회귀모형
정의: 회귀함수가 $f(X) = \beta_{0}+\beta_{1}X$ 선형 형태로 고정된 회귀모형
특징:
- 설명변수 $X$ 가 1개다.
형태:
$Y = \beta_{0} + \beta_{1}X + \epsilon$
- $Y:$ 반응변수
- $\beta_{0}, \beta_{1}:$ 회귀계수
- $X:$ 설명변수
- $\epsilon:$ 잔차
두 회귀계수는 확률변숫값이다. 확률변수 내부에 확률분포를 내포한다. $\beta_{0}, \beta_{1}$ 은 확률분포의 기댓값 모수다. 정확하게 알 수 없다. 즉, 추정의 대상이다.
$\beta_{0}, \beta_{1}$ 이 기댓값 모수이므로, $\beta_{0} + \beta_{1}X$ 의미를 ‘$X$ 에서 $Y$ 기댓값’ 이라고 해석할 수 있다. 이 $Y$ 기댓값에서 잔차 $\epsilon$ 을 더하면 실현된 반응변수 $Y$ 값이 나온다.
기댓값은 모수이므로 정확하게 알 수 없다. 따라서 $\beta_{0} + \beta_{1}X$ 도 정확하게 알 수 없다. 추정 대상이다. $\beta_{0} + \beta_{1}X$ 를 추정하기 위해 $\beta_{0}$ 와 $\beta_{1}$ 기댓값 모수 추정치를 각각 구한다. 그 점 추정치는 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 이라고 하며, 최소제곱추정(최소자승법) 을 이용해서 구한다.
기댓값 모수 점 추정치 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 로 구성된 회귀함수 $\hat{\beta_{0}} + \hat{\beta_{1}}X$ 를 표본회귀함수 라고 하고, $\beta_{0} + \beta_{1}X$ 의 추정치로 삼는다. 표본회귀함수는 $Y$ 기댓값 추정치다.
단순선형회귀모형의 목표는 $Y$ 기댓값 추정치, 그러니까 표본회귀함수 $\hat{\beta_{0}} + \hat{\beta_{1}}X$ 를 찾는 것이다.
한편, 잔차 $\epsilon$ 은 정규분포 $N(0, \sigma^{2})$ 을 따른다고 알려져 있다. $\sigma^{2}$ 은 알 수 없는 모수 값이다. $\sigma^{2}$ 또는 $\sigma$ 를 알면 회귀모형의 대략적인 잔차 크기를 알 수 있다. $\epsilon$ 의 표준편차 $\sigma$ 는 $\epsilon$ 값들이 기댓값 $0$ 에서 대략적으로 떨어진 정도를 의미한다. 즉, $\epsilon$ 의 대략적 크기다. 이 때문에 $\sigma$ 를 알면 회귀모형의 대략적 잔차 크기를 알 수 있는 것이다.
회귀모형의 대략적 잔차 크기를 알면 그 회귀모형이 실현된 데이터를 잘 설명하는지(잘 적합 되었는지) 알 수 있다. 대략적 잔차 크기가 작을 수록, 모형이 주어진 데이터를 잘 설명한다(잘 적합되었다). 모형이 실현된 데이터를 잘 설명하는지 판단. 확인하는 것은 모형 선택에서 중요한 절차다. 모형이 주어진 데이터 잘 설명 못하면 데이터를 더 모으거나, 설정모형을 바꿔야 할 것이다. 따라서 잔차 $\epsilon$ 의 분산모수 $\sigma^{2}$ 또는 표준편차 모수 $\sigma$ 를 아는 것도 중요하다. 종합하면 단순선형회귀모형의 최종 목표는 $\beta_{0}, \beta_{1}, \sigma^{2}$ 을 추정하는 것이다.
단순선형회귀모형 목표 $\Rightarrow$ 3개 모수 $\beta_{0}, \beta_{1}, \sigma^{2}$ 추정
모수추정을 위해. 언제나 그랬듯이, 데이터(표본)를 관측한다. 관측된 표본들과 최소제곱추정(최소자승법) 을 사용해서 모수 추정치를 찾는다.
최소제곱추정(LSE: Least Squares Estimation)
정의: 모형의 잔차 제곱합(총 잔차 크기)을 최소화 시키는 $\beta_{0}, \beta_{1}$ 점 추정치를 찾는 방법
$argmin_{\beta_{0}, \beta_{1}} \sum{(Y_{i}-\hat{Y_{i}})^{2}} = argmin_{\beta_{0}, \beta_{1}} \sum{(Y_{i}-(\hat{\beta_{0}}+\hat{\beta_{1}}X_{i}))^{2}}$
목적함수 $\sum{(Y_{i}-(\hat{\beta_{0}}+\hat{\beta_{1}}X_{i}))^{2}}$ 에 대한 최적화 필요조건은 ‘$\hat{\beta_{0}}, \hat{\beta_{1}}$ 으로 각각 편미분한 1차 도함수가 최적값에서 0이 되어야 한다’ 이다.
1차 도함수를 0 만드는 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 이 최적해(최소해) 이며, 각각 $\beta_{0}, \beta_{1}$ 의 점 추정치다.
목적함수를 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 으로 편미분 한 결과는 아래와 같다.
목적함수를 $D$ 라고 칭하겠다.
편미분 결과
$\frac{\partial{D}}{\partial{\hat{\beta_{0}}}} = -2\sum{(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})} = 0$
$\frac{\partial{D}}{\partial{\hat{\beta_{1}}}} = -2\sum{X_{i}(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})} = 0$
여기서 $\sum{(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})} = 0$ 와 $\sum{X_{i}(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})} = 0$ 를 ‘정규방정식’ 이라고 한다.
정규방정식
- $\sum{(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})} = 0$
- $\sum{X_{i}(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})} = 0$
편미분 결과 1차 도함수를 $0$ 되게 만드는 $\hat{\beta_{0}}$ 과 $\hat{\beta_{1}}$ 을 구하면 아래와 같다.
$\beta_{0}$ 점 추정치(최소제곱추정치) $\hat{\beta_{0}} = \bar{Y}-\hat{\beta_{1}}\bar{X}$
$\beta_{1}$ 점 추정치(최소제곱추정치) $\hat{\beta_{1}} = \frac{\sum{(X_{i}-\bar{X})(Y_{i}-\bar{Y})}}{\sum{(X_{i}-\bar{X})^{2}}} = \frac{S_{XY}}{S_{XX}}$
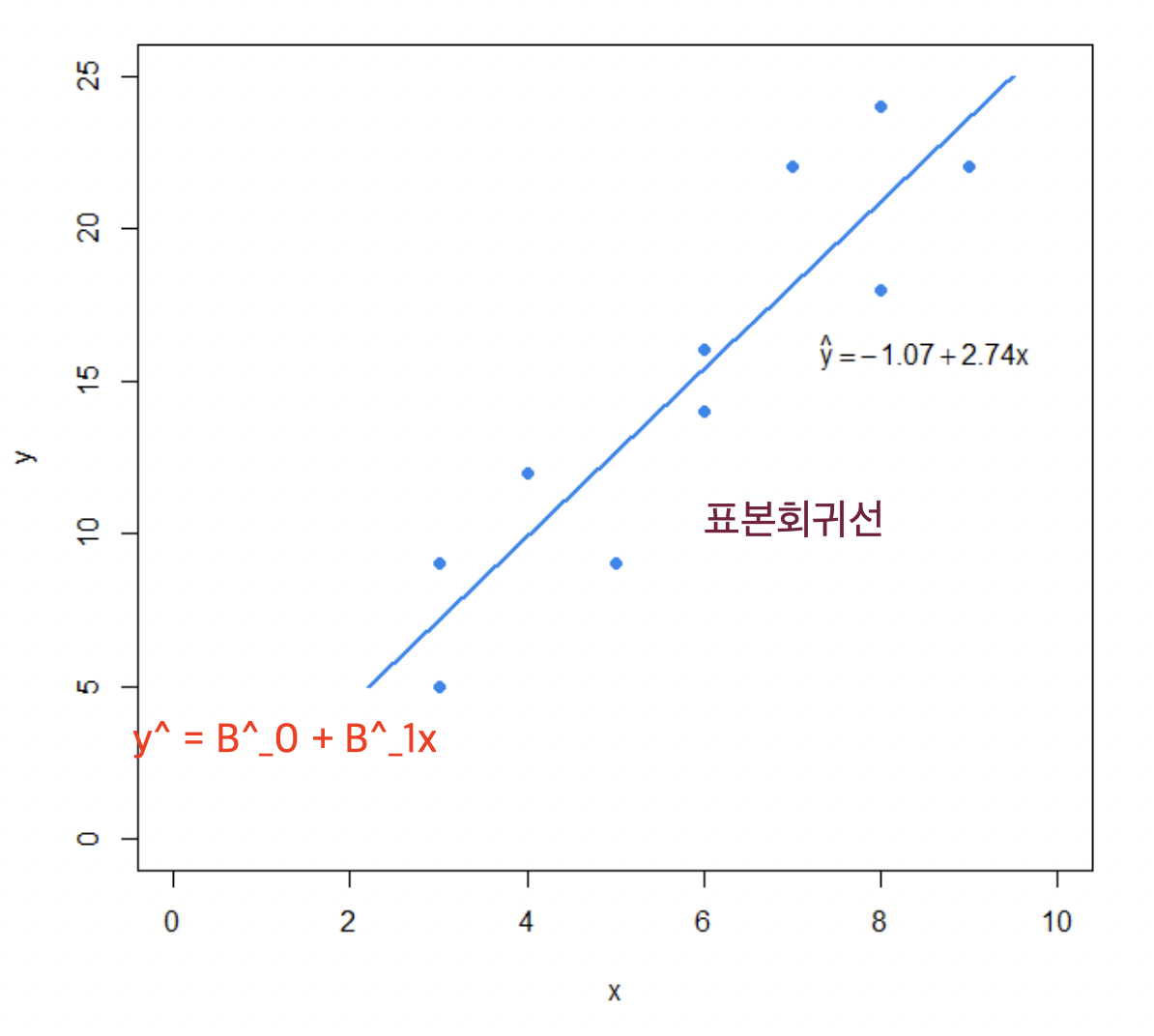
- $\hat{\beta_{0}}$ 과 $\hat{\beta_{1}}$ 을 사용해서 만든 회귀함수 $\hat{\beta_{0}}+\hat{\beta_{1}}X$ 가 표본회귀함수(표본회귀선) 이고 $\hat{\beta_{0}}+\hat{\beta_{1}}X$ 를 회귀함수로 사용한 회귀모형이 적합모형(fitted model) 이다.
$\epsilon$ 분산모수 $\sigma^{2}$ 추정과 $\beta_{0}, \beta_{1}$ 구간추정 및 가설검정
앞에서는 $\beta_{0}, \beta_{1}$ 를 점 추정 했다. 하지만 모수의 점 추정치는 표본 얻을 때 마다 다르며, 여러 개 존재한다. 따라서 점 추정치 이용해서 모수 구간추정 해야 할 필요가 있다.
$\epsilon$ 분산모수 $\sigma^{2}$ 추정
$\epsilon_{i} = Y_{i}-\hat{Y_{i}} = Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i}$
$\epsilon \sim N(0, \sigma^{2})$ 이다.
$\epsilon$ 표본 값들의 비편향 표본분산이 분산모수 $\sigma^{2}$ 의 비편향 추정치가 될 수 있다.
$s^{2} = \frac{1}{(n-2)}\sum{(\epsilon_{i} - 0)^{2}} = \frac{1}{(n-2)}\sum{\epsilon_{i}^{2}} = \frac{1}{(n-2)}\sum{(Y_{i}-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})^{2}}$
- $s^{2}$ 을 구하기 위해서는 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 두 값을 알아야만 한다. 즉, $\hat{\beta_{0}}, \hat{\beta_{1}}$ 는 제약조건이다. $s^{2}$ 을 구하는 데 필요한 표본 수 $n - $ 제약조건 $2$ 개 $=$ 자유도 $(n-2)$ 이다. 그래서 $s^{2}$ 구할 때 $(n-2)$ 로 나누는 것이다.
$\epsilon$ 분산모수 $\sigma^{2}$ 점 추정치 = $s^{2} = \frac{1}{(n-2)}\sum{\epsilon_{i}^{2}}$
$\beta_{1}$ 구간추정
$95$% 신뢰구간을 구하고 싶다면 점 추정치 $\hat{\beta_{1}}$ 이 따르는 분포에서 면적 $0.95$ 에 해당하는 구간을 찾으면 된다.
분포의 면적을 좀 더 쉽게 구하기 위해 $\hat{\beta_{1}}$ 을 표준화 시킨다.
$E[\hat{\beta_{0}}] = \beta_{1}$
$V[\hat{\beta_{1}}] = \frac{s^{2}}{S_{XX}}$
$\frac{\hat{\beta_{1}} - \beta_{1}}{\frac{s}{\sqrt{S_{XX}}}} \sim t(n-2)$
- t분포(통계량)는 $s$ 때문에 자유도가 $(n-2)$ 다.
$\beta_{0}$ 의 $95$% 신뢰구간
$\hat{\beta_{1}} \pm t_{\alpha/2}\frac{s}{\sqrt{S_{XX}}}$
$\beta_{0}$ 구간추정
$\beta_{0}$ 에 대해서도 $\beta_{1}$ 구간추정과 같은 메커니즘을 적용한다.
$E[\hat{\beta_{0}}] = \beta_{0}$
$V[\hat{\beta_{0}}] = s^{2}(\frac{1}{n}+\frac{\bar{x}^{2}}{S_{XX}})$
$\frac{\hat{\beta_{0}} - \beta_{0}}{s\sqrt{\frac{1}{n}+\frac{\bar{x}^{2}}{S_{XX}}}} \sim t(n-2)$
- t분포(통계량)는 $s$ 때문에 자유도가 $(n-2)$ 다.
$\beta_{0}$ 의 $95$% 신뢰구간
$\hat{\beta_{0}}\pm t_{\alpha/2}s\sqrt{\frac{1}{n}+\frac{\bar{x}^{2}}{S_{XX}}}$
$\beta_{0}, \beta_{1}$ 가설검정
$H_{0}: \beta_{i} = \beta_{criterion}$
$H_{a}: \beta_{i} (\ne or > or <) \beta_{criterion}$
- $\beta_{criterion}$ 은 기준값 상수
$\beta_{0}$ 과 $\beta_{1}$ 검정통계량은 두 값의 점 추정치가 된다.
$\beta_{0}$ 검정통계량: $\frac{\hat{\beta_{0}} - \beta_{0}}{s\sqrt{\frac{1}{n}+\frac{\bar{x}^{2}}{S_{XX}}}}$
$\beta_{0}$ 검정통계량 분포: $t(n-2)$
$\beta_{1}$ 검정통계량: $\frac{\hat{\beta_{1}} - \beta_{1}}{\frac{s}{\sqrt{S_{XX}}}}$
$\beta_{1}$ 검정통계량 분포: $t(n-2)$
이제 유의수준 $\alpha$ 를 적절한 값으로 설정하고, $\beta_{0}, \beta_{1}$ 의 유의확률(p-value) 를 구해서
유의확률이 유의수준보다 작으면 귀무가설 기각, 대립가설 채택.
유의확률이 유의수준보다 크면 귀무가설 기각할 수 없음. 으로 결론 지으면 된다.
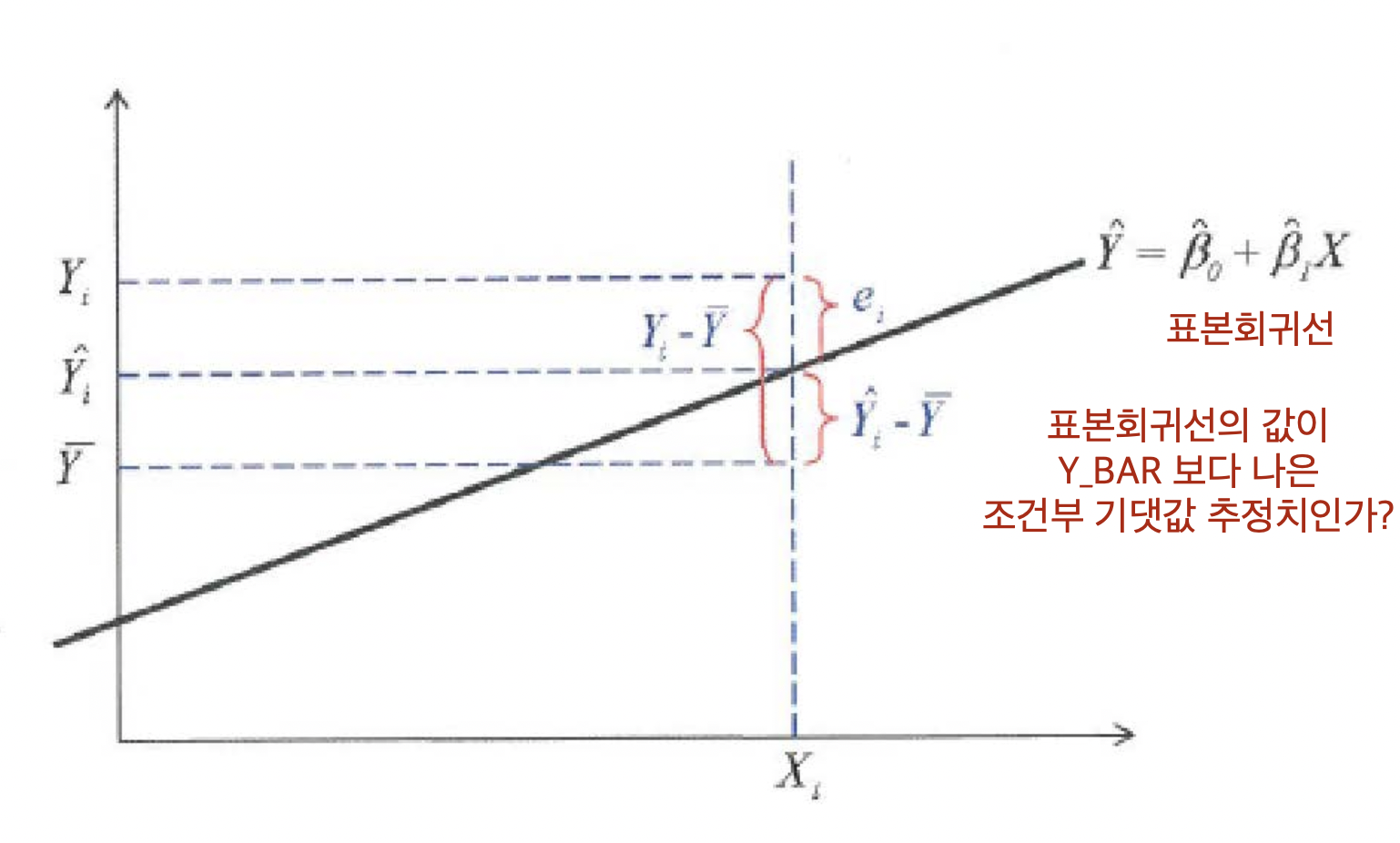
회귀모형의 적합도
정의: 회귀모형 $\hat{Y}$ 이 $\bar{Y}$ 에 비해 더 나은 정도
$\Rightarrow$ 회귀모형이 제공하는 설명력이 $\bar{Y}$ 보다 나은 정도
$\Rightarrow$ 회귀모형이 제공하는 설명력의 정도
회귀모형 적합도는 결정계수 $R^{2}$(또는 $r^{2}$) 로 나타낸다.
$R^{2}$ 결정계수
정의: 회귀모형의 데이터에 대한 적합도(설명력)를 나타내는 값
$R^{2} = \frac{SST}{SST} = 1-\frac{SSE}{SST}$, $(0 < R^{2} < 1)$
- $SST$: 총 제곱합 $\sum{(Y_{i}-\bar{Y}})^{2}$
- $SSR$: 회귀 제곱합 $\sum{(\hat{Y_{i}}-\bar{Y})^{2}}$
- $SSE$: 잔차 제곱합 $\sum{(Y_{i}-\hat{Y_{i}})^{2}}$
- 결정계숫값이 0에 가까울 수록 회귀모형이 X,Y 사이 관계를 제대로 설명 못한다는 말이다.
- 결정계숫값이 1에 가까울 수록 회귀모형이 X,Y 사이 관계를 잘 설명한다는 말이다.
- 단순선형회귀에서는 표본상관계수(피어슨 상관계수) $r$ 값을 제곱하면 결정계숫값과 같아진다.
SST, SSR, SSE 사이 관계와 분산분석 표(ANOVA Table)
회귀모형의 3개 제곱합, SST, SSR, SSE 사이 관계는 아래와 같이 유도할 수 있다.
$Y_{i} - \bar{Y} = \hat{Y_{i}}-\bar{Y} + Y_{i}-\hat{Y}_{i}$
양변을 제곱하면
$(Y_{i} - \bar{Y})^{2} = (\hat{Y_{i}}-\bar{Y})^{2} + (Y_{i}-\hat{Y_{i}})^{2} + 2(\hat{Y_{i}}-\bar{Y})(Y_{i}-\hat{Y_{i}})$
$\sum{(Y_{i} - \bar{Y})^{2}} = \sum{(\hat{Y_{i}}-\bar{Y})^{2}} + \sum{(Y_{i}-\hat{Y_{i}})^{2}} + \sum{2(\hat{Y_{i}}-\bar{Y})(Y_{i}-\hat{Y_{i}})}$
여기서 $\sum{2(\hat{Y_{i}}-\bar{Y})(Y_{i}-\hat{Y_{i})}}$ 은 $0$ 이 된다.
정규방정식으로 cross product term $= 0$ 증명
$\sum{2(\hat{Y_{i}}-\bar{Y})(Y_{i}-\hat{Y_{i}})}$ 에서 $(Y_{i}-\hat{Y_{i}})$ 를 앞으로 분배한다.
$\Rightarrow 2\sum{\hat{Y_{i}}(Y_{i}-\hat{Y_{i}})} - 2\sum{\bar{Y}(Y_{i}-\hat{Y}_{i})}$
정규방정식 1번은 $\sum{(Y_{i}-\hat{Y_{i}})} = 0$ 이었다.
두 번째 항 $2\sum{\bar{Y}(Y_{i}-\hat{Y_{i}})}$ 은 정규방정식 1번에 의해 0 된다.
$2\bar{Y}\sum{(Y_{i}-\hat{Y_{i}})} = 0$
그러면 첫번째 항 $2\sum{\hat{Y_{i}}(Y_{i}-\hat{Y_{i}})}$ 만 남는다.
$\hat{Y_{i}} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{i}$ 를 이용해서 $2\sum{\hat{Y_{i}}(Y_{i}-\hat{Y_{i}})}$ 를 변형시키자.
$\Rightarrow$ $2\sum{(\hat{\beta_{0}}+\hat{\beta_{1}}x_{i})(Y_{i}-\hat{Y_{i}})}$
$(Y_{i}-\hat{Y_{i}})$ 를 앞으로 분배하자.
$\Rightarrow 2\sum{\hat{\beta_{0}}(Y_{i}-\hat{Y_{i}})+2\sum{\hat{\beta_{1}}x_{i}(Y_{i}-\hat{Y_{i}})}}$
위 식에서 첫 번째 항 $2\sum{\hat{\beta_{0}}(Y_{i}-\hat{Y_{i}})}$ 은 앞에서 사용한 정규방정식 1번에 의해 $0$ 된다.
$2\hat{\beta_{0}}\sum{(Y_{i}-\hat{Y_{i}})} = 0$
정규방정식 2번은 $\sum{x_{i}(Y_{i}-\hat{Y_{i}})} = 0$ 이었다.
위 식에서 두 번째 항 $2\sum{\hat{\beta_{1}}x_{i}(Y_{i}-\hat{Y_{i}})}$ 은 정규방정식 2번에 의해 $0$ 된다.
$2\hat{\beta_{1}}\sum{x_{i}(Y_{i}-\hat{Y_{i}})} = 0$
결국 $0+0 = 0$ 된다.
SST, SSR, SSE 사이 관계
$\Rightarrow \sum{(Y_{i} - \bar{Y})^{2}} = \sum{(\hat{Y_{i}}-\bar{Y})^{2}} + \sum{(Y_{i}-\hat{Y}_{i})^{2}}$
- $\sum{(Y_{i} - \bar{Y})^{2}}:$ 총 제곱합(Total Sum of Squares)
- $\sum{(\hat{Y_{i}}-\bar{Y})^{2}}:$ 회귀 제곱합(Regression Sum of Squares)
- $\sum{(Y_{i}-\hat{Y}_{i})^{2}}:$ 잔차 제곱합(Error Sum of Squares)
- 총 제곱합은 $X$ 에 상관없이 고정된 값이다. 총 제곱합이 고정되어 있으므로, 회귀제곱합과 잔차제곱합은 반대로 움직인다. 회귀모형 적합도가 높아지면 회귀제곱합이 커지고 잔차 제곱합이 작아진다. 반대도 성립한다.
각 제곱합의 자유도
- 총 제곱합: $\bar{Y}$ 때문에 제약조건이 1개 있다. 따라서 $n-1$
- 잔차 제곱합: $\hat{Y_{i}} = \hat{\beta_{0}}+\hat{\beta_{1}}x_{i}$ 이었다. $\hat{Y_{i}}$ 을 구하려면 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 이 필요하다. 따라서 제약조건이 2개다. 자유도$: n-2$
- 회귀 제곱합: 총 제곱합 자유도$(n-1)$ - 잔차 제곱합 자유도$(n-2)$ $=1$ 이다.
분산분석표(ANOVA Table) 을 이용하면 위 관계와 각 제곱합의 자유도, 평균제곱, F비를 한번에 나타낼 수 있다.
회귀의 분산분석표
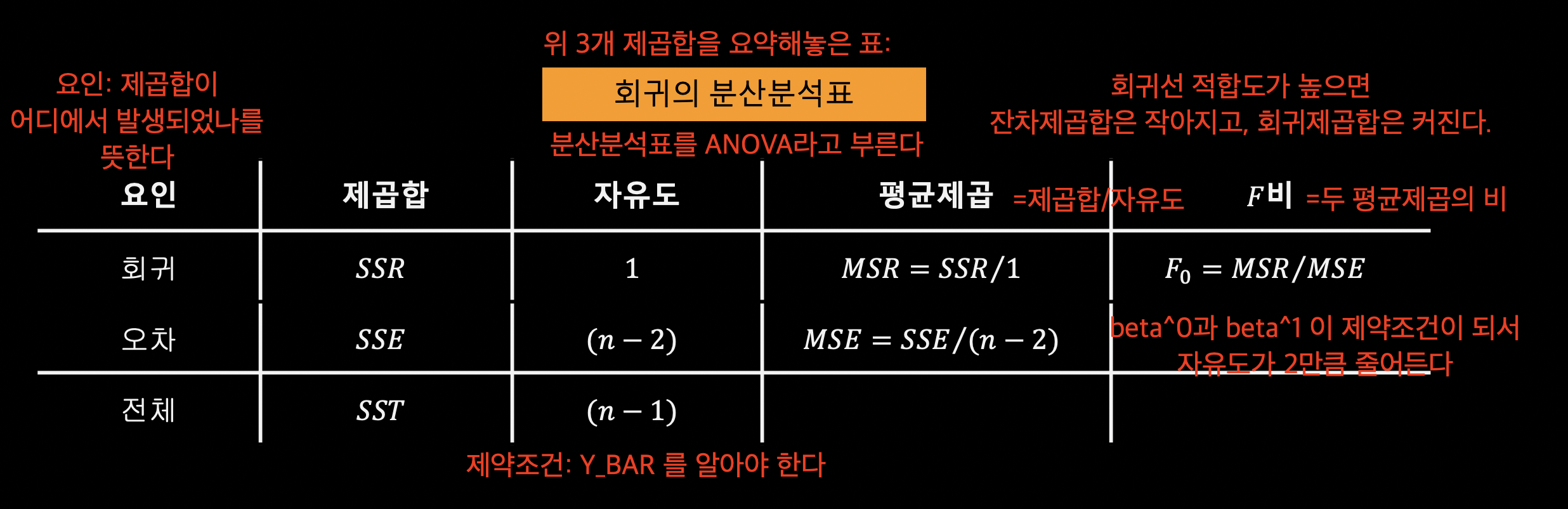
[이미지 출처: 부산대학교 김충락 교수님의 R을 이용한 통계학개론 - 07_회귀분석.pdf 23 페이지]
평균제곱: $\frac{제곱합}{자유도}$
$F$비: $\frac{MSR}{MSE}$, 모형 전체의 통계적 유의성을 검정할 때 사용한다.
$R^{2}$ 결정계수: $\frac{SSR}{SST} = 1-\frac{SSE}{SST}$
R에서 단순선형회귀분석 하기
1
2
3
4
5
6
7
8
9
10
# 단순선형회귀분석
x <- c(3,3,4,5,6,6,7,8,8,9)
y <- c(9,5,12,9,14,16,22,18,22,24)
length(x);length(y)
# 단순선형회귀모형으로 적합
fit <- lm(y~x) # y: 종속변수 , x: 설명변수
summary(fit)
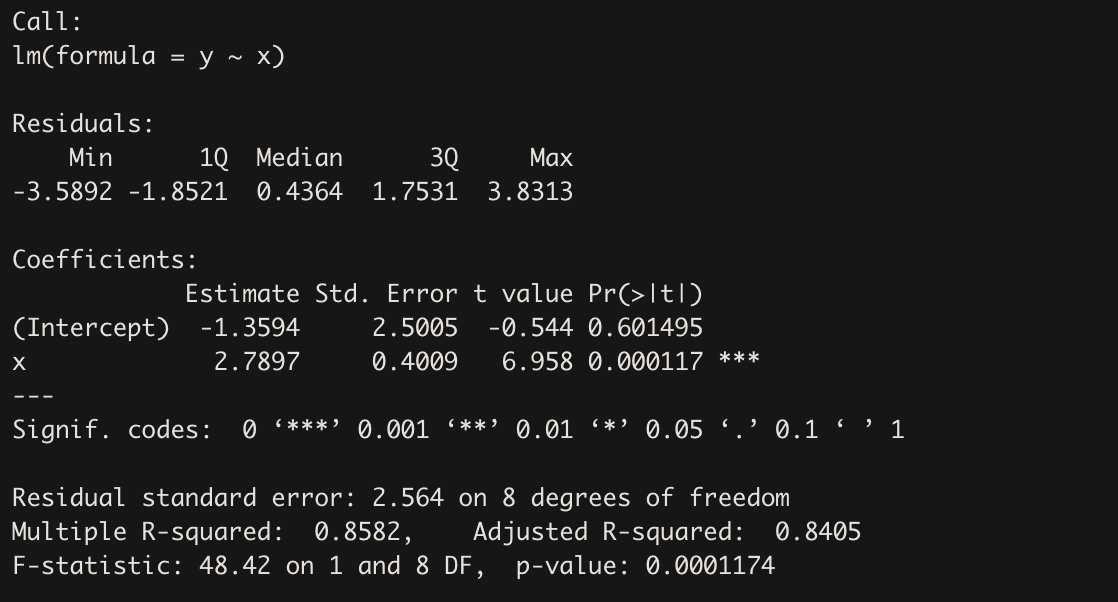
summary() 결과 설명
Residuals
$Y_{i} - \hat{Y_{i}}$ 잔차 값들의 최솟값, 1분위수, 중앙값, 3분위수, 최댓값 출력
Coefficients
최소제곱추정으로 구한 회귀계수 추정치 $\hat{\beta_{0}}, \hat{\beta_{1}}$ 출력한다.
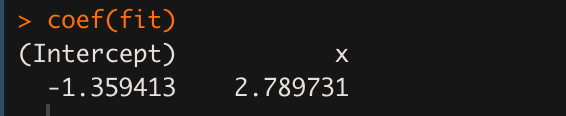
Intercept 가 $\hat{\beta_{0}}$ 에 해당하고, x 가 $\hat{\beta_{1}}$ 에 해당한다. 각각 -1.3594, 2.7897 이 나왔다(Estimate).
한편 두 점 추정치를 표준화 한 $t$ 통계량 값도 볼 수 있다(t value). 각각 -0.544, 6.958 이다. 둘 다 자유도 8(10-2)인 $t$ 분포를 따른다.
이 $t$ 통계량을 검정통계량, $t$ 분포를 검정통계량분포로 삼았을 때 유의확률이 가장 오른쪽 값이다. 각각 0.601495, 0.000117 이 나온 걸 관찰할 수 있다. 그리고 그 유의확률에 따른 귀무가설 기각 여부를 별(*) 표시로 알 수 있다.
여기서 귀무가설은 $H_{0}: \hat{\beta_{i}} = 0$ (회귀계수가 의미 없다) 가 된다. 대립가설은 ‘회귀계수는 통계적으로 유의미하다’가 된다. Intercept는 별이 없다. 유의확률 값이 커서 회귀계수가 통계적으로 유의미하지 않다. 반면 X 는 별이 있다. 유의확률값이 작아서 $\hat{\beta_{1}}$ 이 통계적으로 유의미함을 나타낸다.
각 회귀계수의 통계적 유의성에 따라, 회귀모형은 최종으로 $\hat{Y_{i}} = \hat{\beta_{1}}X_{i}$ 가 된다.
Residual standard error
잔차의 표본표준편차 $s$ 를 말한다. 회귀모형이 대체로 어느 정도의 잔차를 갖는지 알려준다. $s = 2.564$ 가 나왔다. 그리고 $s$ 의 자유도는 8(10-2) 가 나온다.
Multiple R-squared
결정계숫값 $R^{2}$ 이다. 0.8592 가 나왔다. 회귀모형의 설명력이 꽤 높은 편이다.
Adjusted R-squared
다중회귀모형의 경우 모형에 여러 변수를 많이 넣으면 많이 넣을 수록, 개별 독립변수 $X_{i}$ 의 $Y$ 에 대한 설명력 유무에 관계 없이 모형의 결정계숫값(설명력) 이 올라가는 경향이 나타난다.
즉, 모형에 포함된 어떤 $X_{i}$ 가 $Y$ 설명에 별 도움이 안되는데도 모형에 설명변수를 많이 넣었다는 이유 만으로 모형의 ‘설명력이 높다’고 나올 수 있다.
이 문제를 해결하기 위해 사용하는 게 조정된 결정계숫값이다. 조정된 결정계숫값은 개별 변수의 데이터 수 보다 변수 갯수가 더 많아지면(선형종속 발생 환경), 추가되는 설명변수에 대해 패널티를 부여해서 값을 산출한다.
다중선형회귀모형 일 때는 결정계숫값과 조정된 결정계숫값 두 가지를 모두 보는 것이 좋다. 만약 두 값 사이 차이가 크다면, 종속변수 $Y$ 설명에 별 도움 안 되는 설명변수 $X$ 가 모형에 끼어있을 수 있을 수 있다.
F-statistic
F비 값이다. $F = \frac{MSR}{MSE}$. 모형 전체의 통계적 유의성을 검정할 때 사용한다.
귀무가설은 ‘$\hat{\beta_{0}}$ 을 제외한 모든 회귀계숫값 = 0(통계적 관점에서, 모형이 유의미하지 않다)’, 대립가설은 ‘최소한 회귀계수 하나는 0이 아니다(통계적 관점에서, 모형이 유의미하다)’ 이다.
F비 값이 따르는 F 분포는 자유도로 (MSR자유도, MSE자유도) 를 갖는다. 이 경우에는 회귀제곱합의 자유도 1, 잔차제곱합의 자유도 8 이라서 DF가 1 and 8로 나왔다.
F분포 상에서 F비 값 48.48의 유의확률은 0.0001174로, $\alpha = 0.05, 0.01, 0.1$ 세 유의수준보다 모두 낮다. 따라서 이 회귀모형은 통계적 유의성을 갖는다.
1
2
3
4
5
# 잔차 출력
resid(fit)
# 또는
rr <- y - fitted(fit);rr
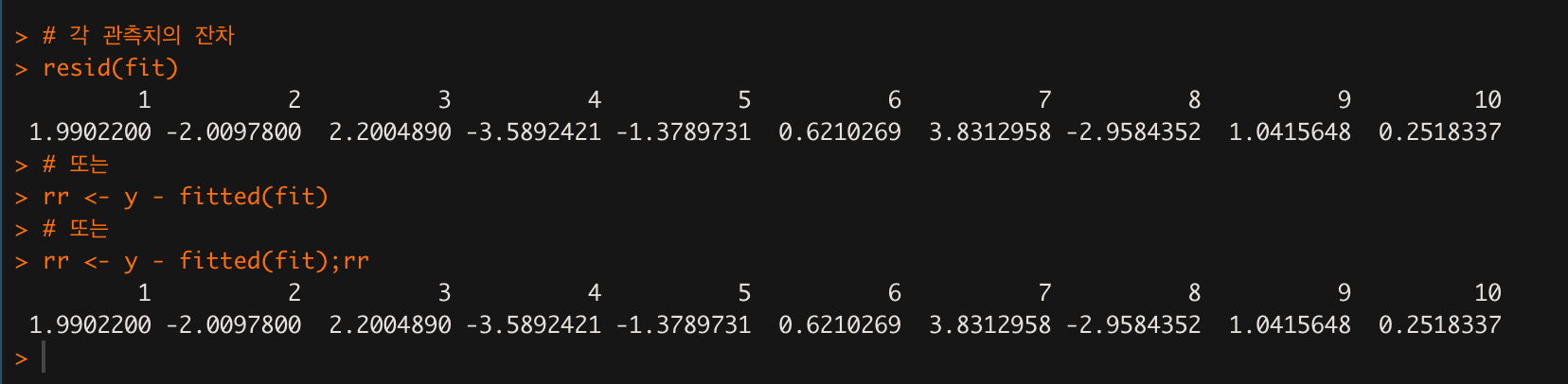
resid() 명령은 잔차 $\epsilon_{i}$ 를 출력해준다.
1
2
3
4
5
# 회귀계수 만 출력
coef(fit)
# 또는
fit$coefficients
1
2
# 회귀계수의 신뢰구간
confint(fit, level=0.95)

1
2
3
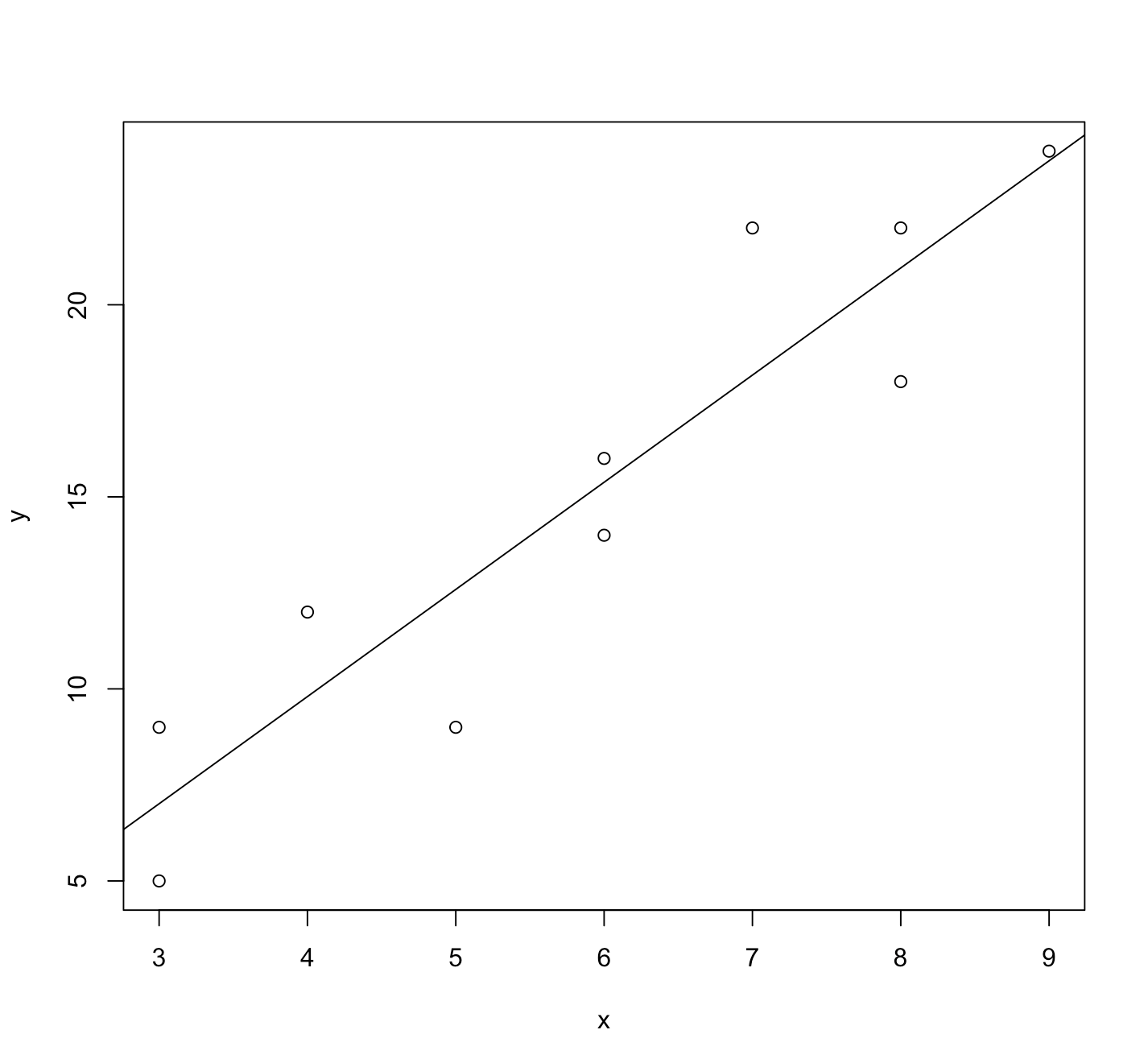
# 산점도에 표본회귀선을 그리고 싶을 때
plot(x,y)
abline(fit)
1
2
# 분산분석표 ANOVA Table
anova(fit)
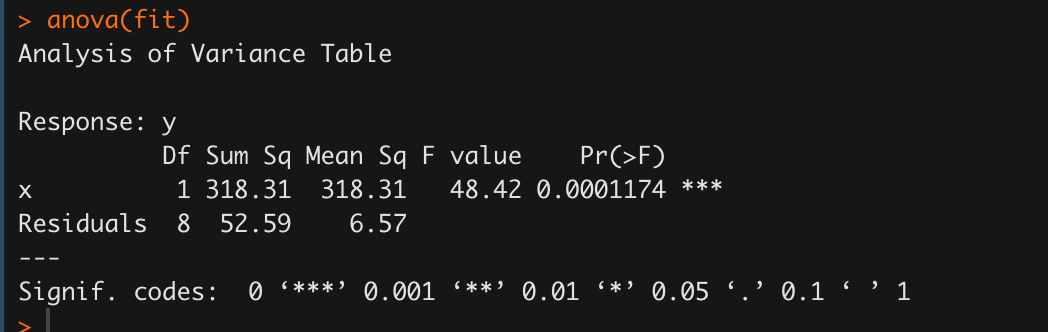
요인 중 회귀와 잔차(오차)가 제시된 분산분석표를 볼 수 있다.
참고)

모수회귀모형 - 다중선형회귀모형
p개 변수 관측치 벡터의 선형조합.
$Y = \beta_{0}1+\beta_{1}X_{1}+\beta_{2}X_{2}+…\beta_{p-1}X_{p-1}+\epsilon$
- $X_{i}$ 는 $i$ 번째 변수의 관측치 벡터
- $\beta_{i}$ 는 다른 변수와 독립적으로 변수 $X_{i}$가 1 증가할 때 $Y$ 가 증가하는 양
- $\beta_{i}$ 는 스칼라 값, $1$ 과 $X_{i}$ 는 벡터
위 식을 행렬 이용해서 아래와 같이 나타낼 수도 있다.
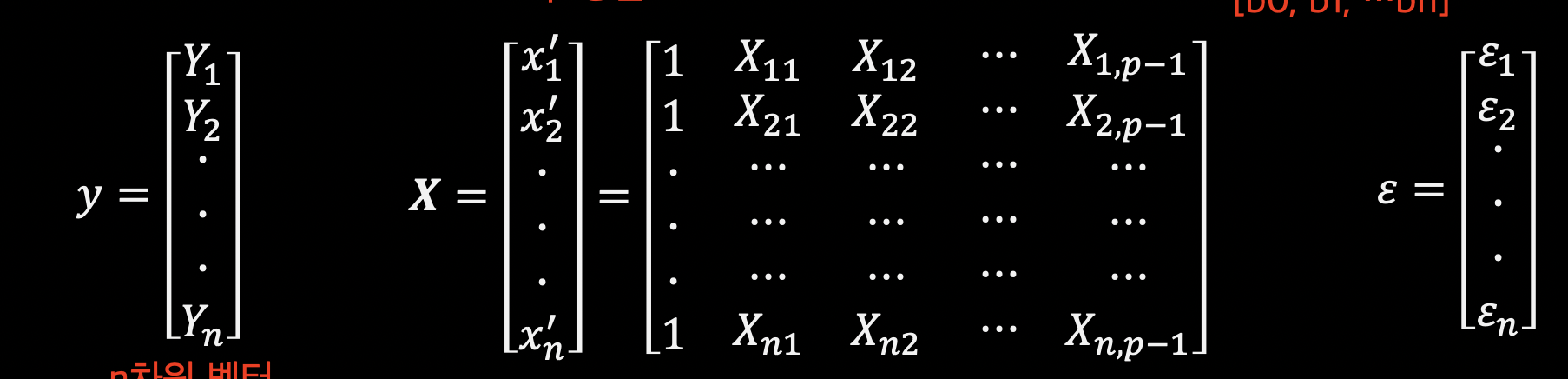
[이미지 출처: 부산대학교 김충락 교수님의 R을 이용한 통계학개론 - 07_회귀분석.pdf 28페이지]
$Y = X\beta + \epsilon$
- $Y$ 는 $(n \times 1)$ 차원 벡터
- $X$ 는 $p-1$ 개 변수의 $n$ 개 관측치로 구성된 $(n\times p)$ 차원 행렬
- $\beta$ 는 각 변수의 가중치로 구성된 $(p\times{1})$ 벡터
- $\epsilon$ 은 관측치 $Y_{i}$와 $Y$ 기댓값 예측치 사이 잔차값들로 구성된 $(n\times{1})$ 벡터
다중선형회귀모형의 최종 목표:
가중치 벡터 $\beta$ 를 찾는 것.
가중치 벡터 $\beta$ 는 알 수 없는 모수 값들로 구성되어 있다.
$\beta = [\beta_{0}, \beta_{1}, \beta_{2}, … \beta_{p-1}]^{T}$
따라서 단순선형회귀분석에서 회귀계수 $\beta_{0}$ 과 $\beta_{1}$ 을 찾을 때와 마찬가지로, ‘추정’ 해야 한다.
가중치 벡터 $\beta$ 를 추정하는 방법은 단순선형회귀분석과 마찬가지로, 잔차 제곱합(잔차 총 크기)가 최소가 되는 $\beta$ 를 찾는 것이다.
잔차 총 크기 = 잔차 벡터 $norm^{2}$ 하면 얻을 수 있다.
${\vert{\epsilon}\vert{}}^{2} = \sqrt{요소 제곱합}^{2} =$ 요소제곱합
$\Rightarrow \sum{\epsilon_{i}^{2}} = \epsilon^{T}\epsilon$
위에서 $Y = X\beta+\epsilon$ 이었다. $X\beta$ 를 좌변으로 넘기면
$\epsilon = Y-X\beta$ 가 된다.
$\Rightarrow \epsilon^{T}\epsilon = (Y-X\beta)^{T}(Y-X\beta)$
목표는 $(Y-X\beta)^{T}(Y-X\beta)$ 가 최소가 되는 $\beta$ 를 찾는 것이다.
$argmin_{\beta}{(Y-X\beta)^{T}(Y-X\beta)}$
$\Rightarrow (Y-X\beta)^{T}(Y-X\beta) = (Y^{T}-\beta^{T}X^{T})(Y-X\beta)$
앞의 괄호를 뒤로 분배하면
$Y^{T}Y-Y^{T}X\beta-\beta^{T}X^{T}Y + \beta^{T}X^{T}X\beta$
두번째 항 $Y^{T}X\beta$ 는 스칼라 값이다. 통째로 전치연산 해도 같다.
$= Y^{T}Y-(Y^{T}X\beta)^{T}-\beta^{T}X^{T}Y + \beta^{T}X^{T}X\beta$
$= Y^{T}Y-\beta^{T}X^{T}Y-\beta^{T}X^{T}Y + \beta^{T}X^{T}X\beta$
최적화(최소화) 목적함수: $Y^{T}Y-2\beta^{T}X^{T}Y+ \beta^{T}X^{T}X\beta$
최적화 필요조건인 기울기 필요조건을 만족하는 $\beta$ 를 찾자.
$\beta$ 로 편미분 한 1차 도함수가 0 되는 $\beta$ 를 찾아야 한다.
$\frac{\partial{목적함수}}{\partial{\beta}} = -2X^{T}Y+2X^{T}X\beta = 0$
$2X^{T}X\beta = 2X^{T}Y$
$X^{T}X\beta = X^{T}Y$
$X^{T}X$ 는 $(p\times{p})$ 크기 정방행렬이다. 만약 $X^{T}X$ 행렬의 역행렬이 존재한다면 아래와 같이 처리할 수 있다.
$\beta = (X^{T}X)^{-1}X^{T}Y$
위 $\beta$ 가 최적해(최소해) 다. 잔차 제곱합(총 잔차 크기)을 최소로 만드는 $\beta$ 다.
가중치 벡터 $\beta$ 의 추정치 이다.
$\hat{\beta} = (X^{T}X)^{-1}X^{T}Y$
다중선형회귀에서 SST, SSR, SSE 사이 관계와 분산분석표
SST, SSR, SSE 사이 관계
단순선형회귀분석과 같다. 다만 자유도가 다르다.
$\sum{(Y_{i}-\bar{Y})^{2}}= \sum{(\hat{Y_{i}}-\bar{Y})^{2}}+\sum{(Y_{i}-\hat{Y_{i}})^{2}}$
- $\sum{(Y_{i}-\bar{Y})^{2}}$: 총제곱합(SST)
- $\sum{(\hat{Y_{i}}-\bar{Y})^{2}}$: 회귀제곱합(SSR)
- $\sum{(Y_{i}-\hat{Y_{i}})^{2}}$: 잔차제곱합(SSE)
- 총제곱합은 $X$ 관계없이 고정된 값이다. 따라서 회귀제곱합과 잔차제곱합은 반대로 움직인다.
자유도
- SST: $(n-1)$, $\bar{Y}$ 가 제약조건 1
- SSE: $(n-p)$, $\hat{Y_{i}} = \hat{\beta_{0}}+\hat{\beta_{1}}X_{i, 1}+\hat{\beta_{2}}X_{i,2}+…+\hat{\beta_{p-1}}X_{i,p-1}$ 이다. $\hat{Y_{i}}$ 값을 구하기 위해서는 $\hat{\beta_{0}}, \hat{\beta_{1}}, …\hat{\beta_{p-1}}$ 의 $\hat{\beta_{i}}$ $p$ 개를 알아야 한다. 따라서 제약조건도 $p$ 개다. 자유도는 $(n-p)$ 가 된다.
- SSR: $(n-1)-(n-p) = (p-1)$ 이다.
분산분석표(ANOVA Table)

[이미지 출처: 부산대학교 김충락 교수님의 R을 이용한 통계학개론 - 07_회귀분석.pdf 30페이지]
F비
F비 값 $\frac{MSR}{MSE}$ 은 다중회귀모형의 유의미성을 검정할 때 사용한다. 귀무가설이 맞다는 전제 하에, F비 값은 $F(p-1, n-p)$ 를 따른다.
$F statistic = \frac{MSR}{MSE} \sim F(p-1, n-p)$
다중회귀모형의 유의성 검정
다중회귀모형이 의미가 있는지 없는지 검정한다.
$H_{0}: \hat{\beta_{1}} = \hat{\beta_{2}}= … \hat{\beta}_{p-1} = 0$ (다중회귀모형이 의미가 없다)
$H_{a}: \hat{\beta_{i}}$ 중 최소한 하나는 $0$ 이 아니다 (모형이 의미가 있다)
귀무가설 기각하려면 $F$ 비 값이 매우 커야 한다.
$F$ 비 값은 $\frac{MSR}{MSE}$ 이다.
$F$ 비 값이 커지려면 $MSR$이 커져야 한다. $MSR$이 커지려면 $SSR$ 이 커져야 한다. $\Rightarrow$ $F$ 비 값이 커지려면 $SSR$ 이 매우 커져야 한다.
한편 $F$ 비 값이 커지려면 $MSE$ 는 작아져야 한다. $MSE$ 가 작아지려면 $SSE$ 가 작아져야 한다. $\Rightarrow$ $F$ 비 값이 커지려면 $SSE$ 가 매우 작아져야 한다.
종합하면, $F$비 값이 커져서 귀무가설을 기각(모형이 의미가 있다) 하려면 $SSR$ 값이 커지고 $SSE$ 값이 작아져야 한다.
R에서 다중회귀분석
R 내장 stackloss 데이터
1
2
3
# 다중회귀분석
dt = stackloss # R 내장 stackloss 데이터
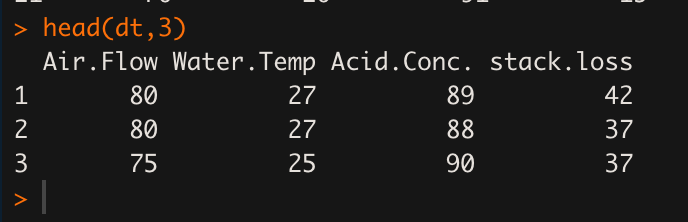
head(dt,3) # air flow, water temp, acid.conc, stackloss 4개 변수의 데이터로 구성된 데이터셋이다.
반응변수와 설명변수 설정
1
2
3
4
5
# 반응변수
y <- dt$stack.loss
x1 <- dt$Air.Flow
x2 <- dt$Water.Temp
x3 <- dt$Acid.Conc.
데이터(관측치) 행렬 X 생성
1
2
# 데이터 행렬
X <- cbind(x1, x2, x3) # 열벡터 x1, x2, x3를 열로 써서 묶어라 (행렬로 변환)
x1, x2, x3 변수 사이 관계 모아보기
1
2
# 각 변수 사이 관계 산점도로 살펴보기
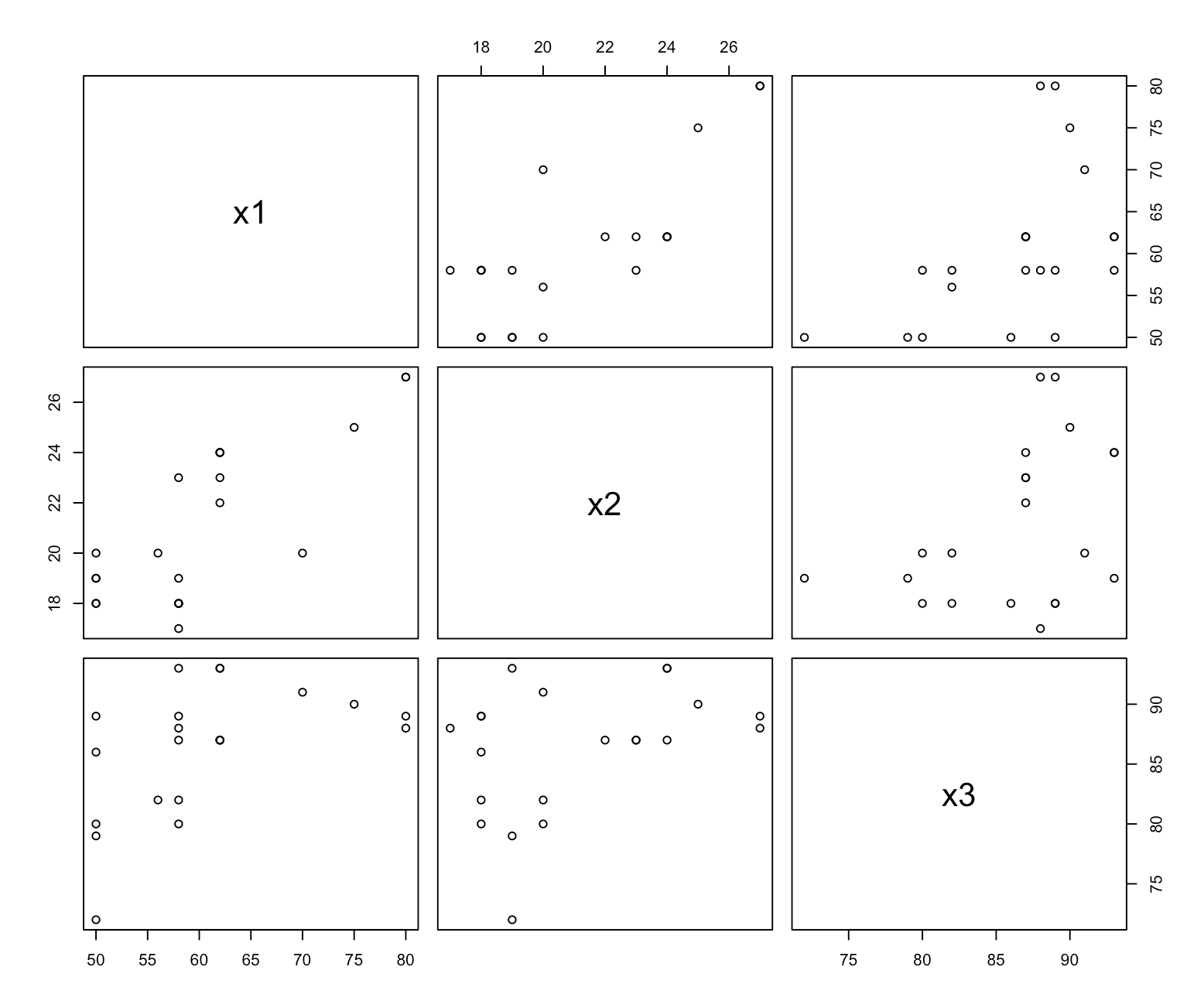
pairs(X)
x1, x2, x3 중 서로 상관관계 있어 보이는 변수들은 y에 대한 설명이 중복될 수 있다.
따라서 스캐터 플롯으로 결과를 보고, 서로 상관관계 있어보이는 x 변수들은 모형에 둘 중 하나만 넣거나 둘 다 빼는 걸 고려해 볼 수 있다.
다중선형회귀모형에 반응변수와 설명변수 회귀시키기
1
2
3
4
# 다중선형회귀모형
stackfit<-lm(y~x1+x2+x3) # 반응변수~ 설명변수 1,2,3
plot(stackfit)
plot(회귀모형) 명령은 아래 4개 플롯을 제공한다.
- Residual vs Fitted
- Normal Q-Q plot
- Standardized Residual vs Fitted
- Residuals vs Leverage
Residual vs Fitted
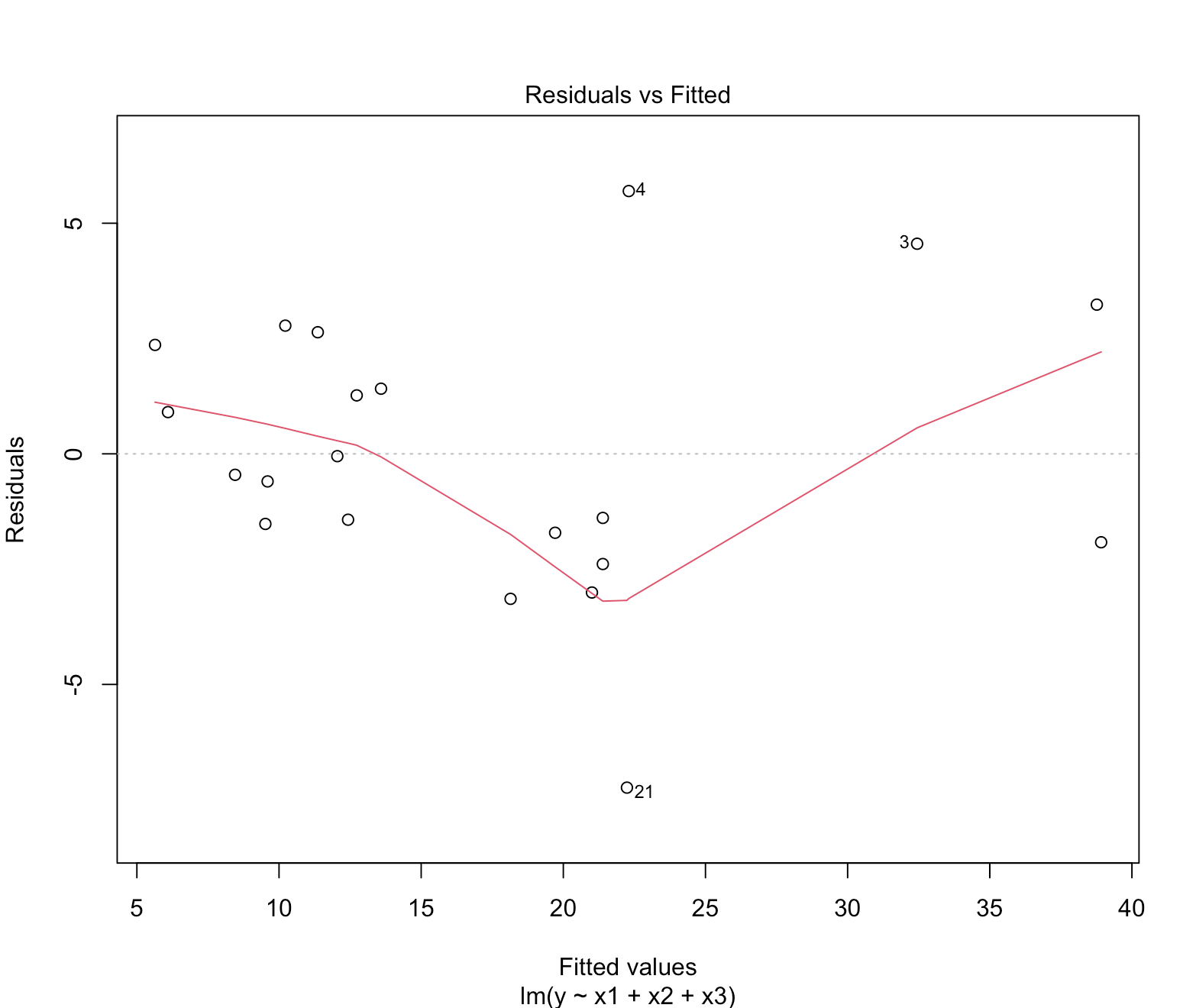
Residual vs Fitted plot 은 $\hat{y}$ 값 별 잔차를 보여준다.
그래프에서 $y$ 축이 잔차 크기를 나타낸다. 잔차 크기가 $-2$ 에서 $2$ 를 넘어서면 아웃라이어 값이라고 본다.
Normal Q-Q plot
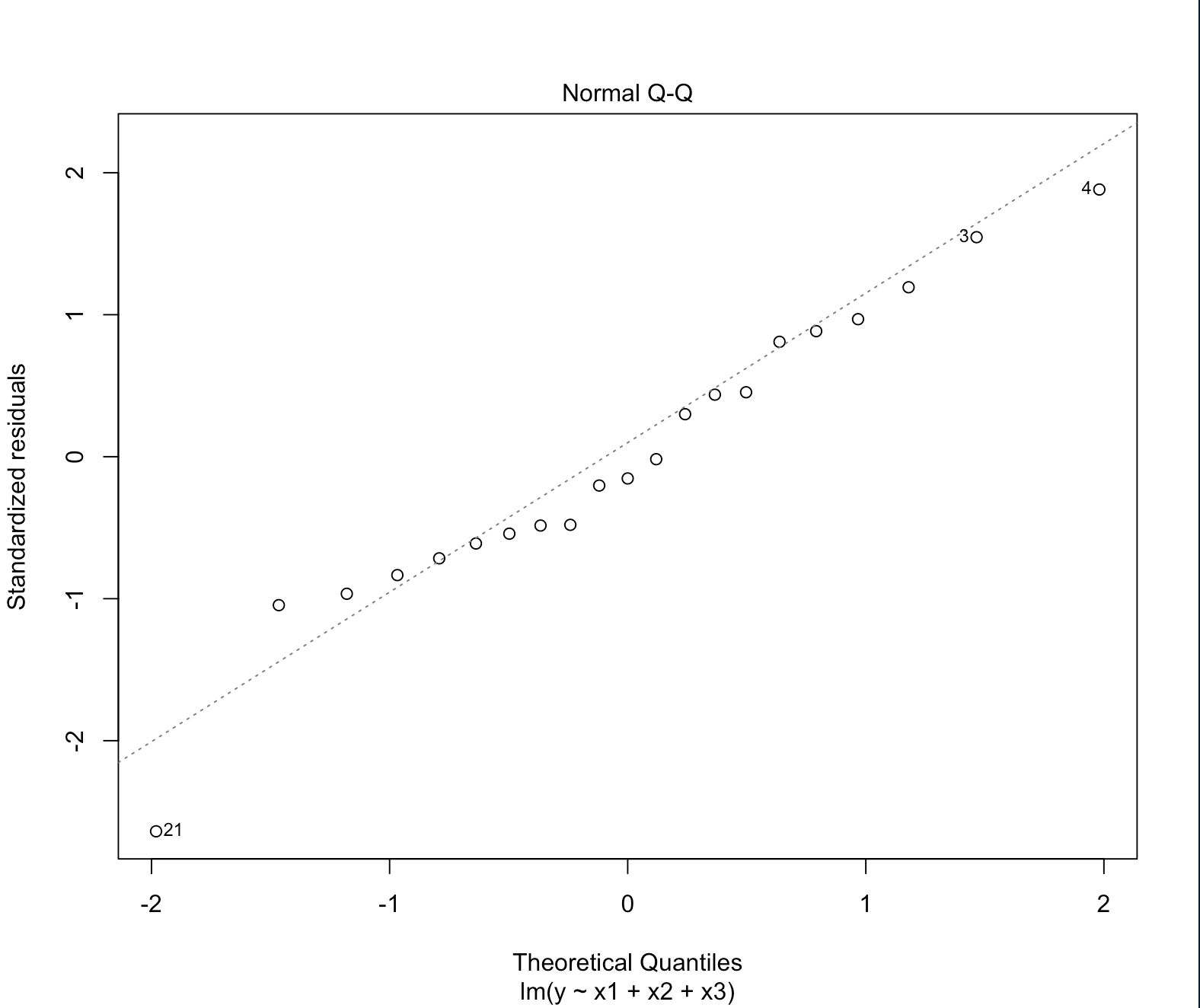
Normal Q-Q plot 은 잔차의 표본분포가 정규분포를 따르는지 보여준다.
잔차는 이론적으로 정규분포 $N(0, \sigma^{2})$ 을 따른다고 했었다.
이 그래프는 잔차가 정규성 가정을 만족하는지 보여준다.
선형에 가까울 수록 정규분포에 가까운 것이다.
Standardized Residual vs Fitted
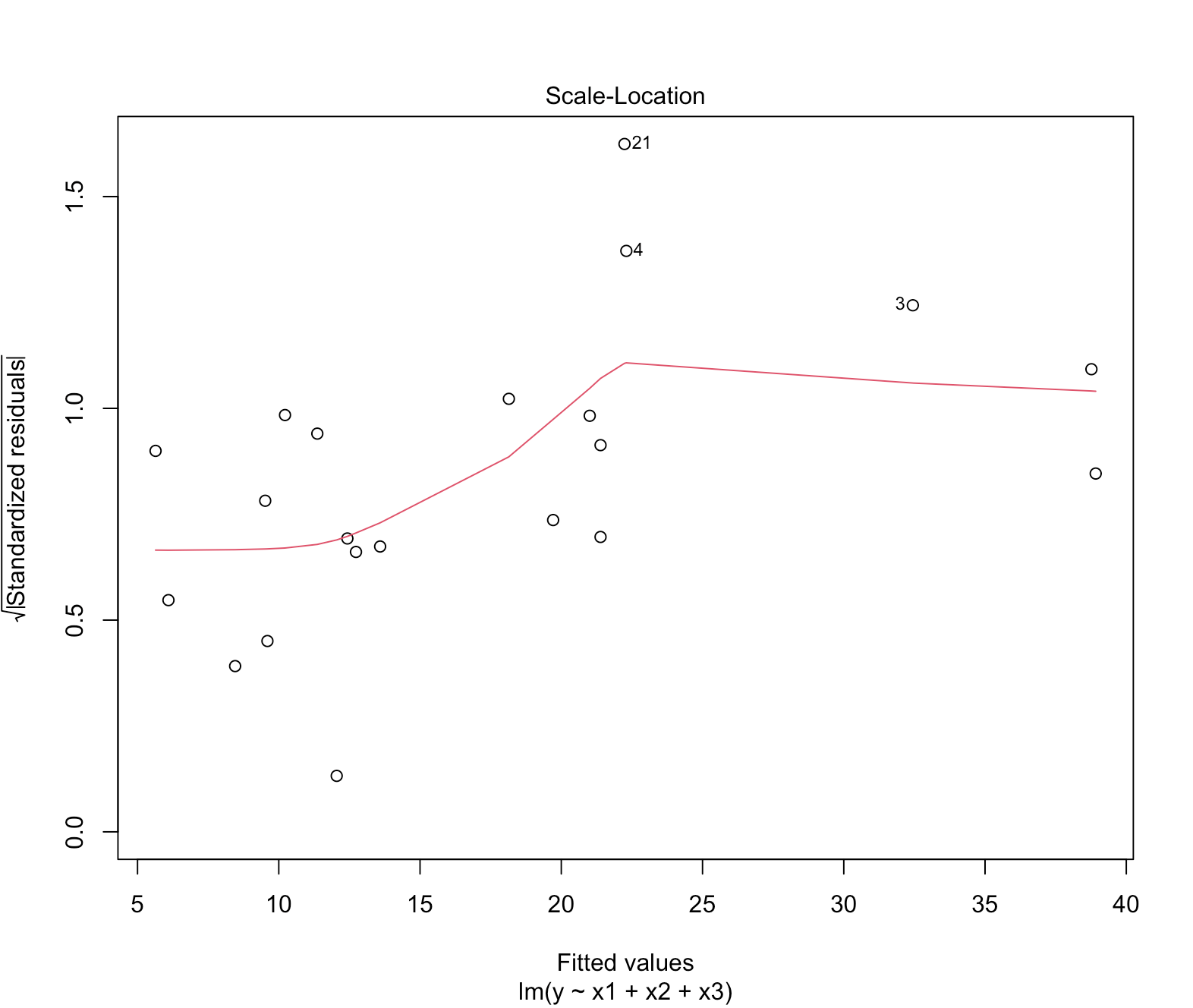
Standardized Residual vs Fitted plot 은 $\hat{y}$ 값 별 표준화 잔차를 보여준다.
$y$ 축이 표준화 잔차 크기를 나타낸다.
잔차를 표준화 시키는 방법은 아래와 같다.
$r$ 을 잔차라고 칭할 때,
표준화 잔차 $= \frac{\vert{r}\vert{}}{잔차의 표준오차}$
표준화 잔차 절댓값이 $0$ 기준으로 $2, 2.5,$ 또는 $3$ 을 넘어서는 fitted value를 아웃라이어 값이라고 본다.
위 그래프는 표준화 잔차에 제곱근을 취했다. 따라서 $\sqrt{표준화잔차}$ 가 대략 $1 \sim 1.2$ 인 값들이 아웃라이어 값들이다.
Residuals vs Leverage
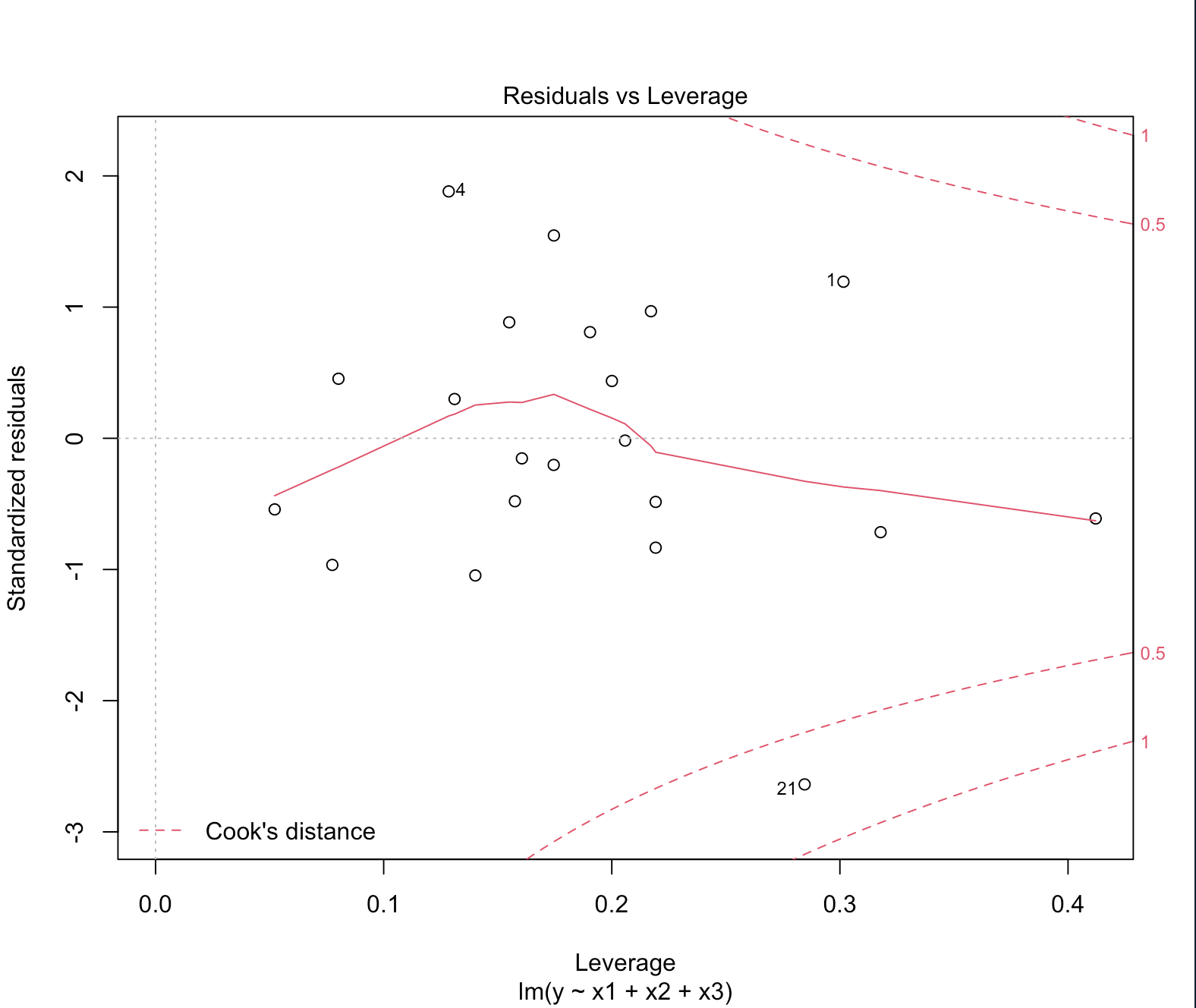
그래프 X 축(Leverage)은 설명변숫값이 평균에서 떨어져 있는 정도를 의미한다. 레버리지가 클 수록 평균에서 멀리 떨어져 있다는 뜻이다.
한편 그래프 상에 붉은 점선으로 된 컨투어 플롯이 쿡 거리를 나타낸다. 맨 가운데 붉은 실선에서 멀어지면 멀어질 수록 쿡 거리가 먼 것(쿡 통계량이 큰 것) 이다. $21, 4, 1$ 이 다른 값들보다 쿡 통계량이 큰 값들이다. 한편 $1$ 과 $21$ 관측치는 레버리지가 크고, 잔차도 상당히 큰 값들이다. $4$ 관측치는 레버리지는 작지만 잔차가 큰 값이다.
- 쿡 통계량: $\hat{\beta}$ 값에 유독 영향 많이 미치는 관측치가 뭔지 알려주는 척도다.
1
2
# 추정 결과 요약
summary(stackfit)
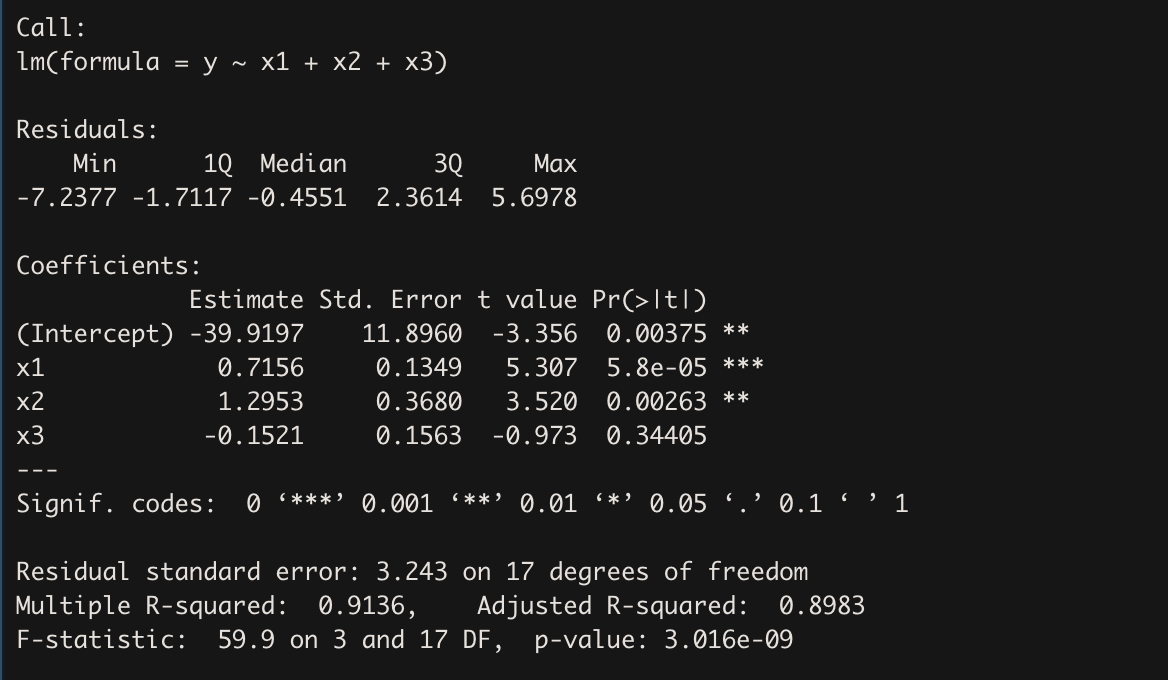
회귀계수 검정 결과를 볼 때, 이 회귀모형은 사실상
$Y = \hat{\beta_{0}} + \hat{\beta_{1}}X_{1}+\hat{\beta_{2}}X_{2}$ 와 같다. $\hat{\beta_{3}}$ 는 통계적 관점에서 볼 때 의미가 없었다.
1
2
# 분산분석표
anova(stackfit)
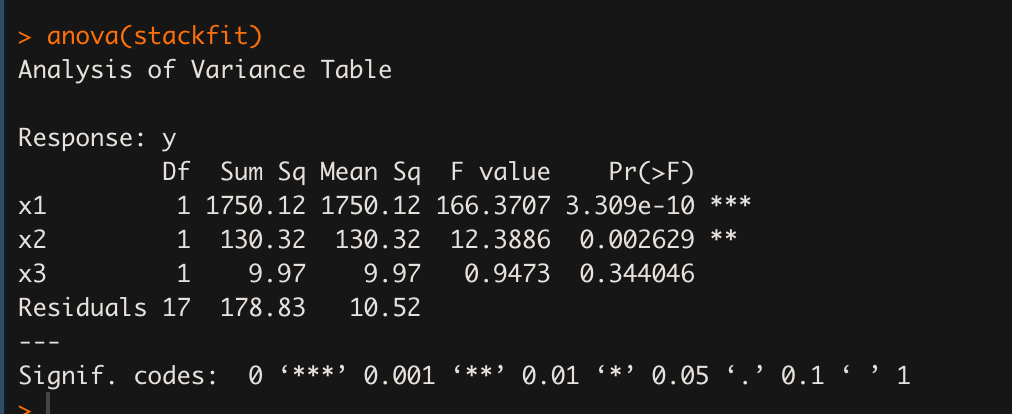
위 분산분석표는 (x1, residuals), (x2, residuals), (x3, residuals) 해서 각각 F비를 계산하고 각 변수의 회귀계수가 유의한지 F 분포를 이용해 검정, F비의 p-value 를 나타낸 결과다.
summary() 결과와 마찬가지로 변수 x1과 x2가 통계적으로 유의미하게 나왔다.
1
2
# 회귀모형의 잔차제곱합
deviance(stackfit) # stackfit은 y_hat 값들이다. sum(y-y_hat)^{2} 즉 잔차제곱합 계산한다.
178.83
1
2
# 회귀모형의 총제곱합
deviance(lm(y~1)) # lm(y~1) 은 y 평균 y_bar 를 의미한다. 따라서 이 명령은 sum(y-y_bar)^{2} 총제곱합을 의미한다.
2069.238
1
2
# 회귀모형의 모든 잔차
residuals(stackfit)
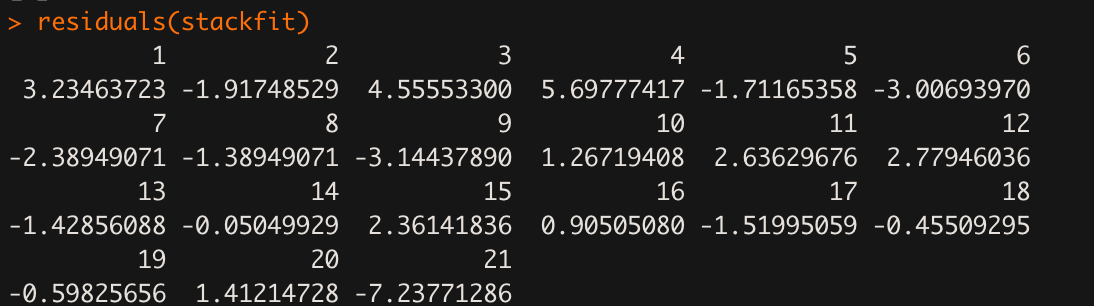
1
2
# 회귀계숫값들의 분산-공분산 행렬
vcov(stackfit)

1
2
# 회귀계숫값들
coef(stackfit)

1
2
# step: 실질적으로 y 설명하는 독립변수만 남겨서 출력하는 명령
step(stackfit)
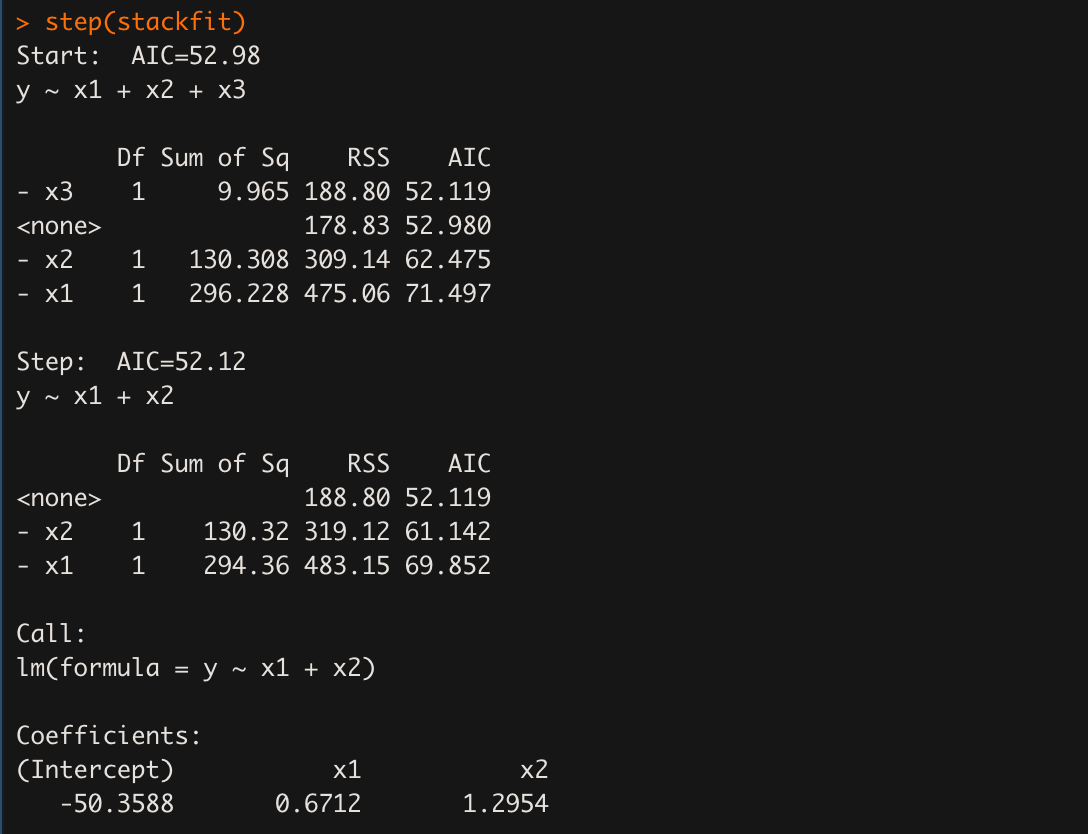
intercept, x1, x2 의 회귀계수만 남아서 출력되었다.
이는 분산분석표에서 관찰했던 것과 같다.
2차원 평면에서 그림 그리기
1
2
3
# 데이터셋 로드
faithful
head(faithful)
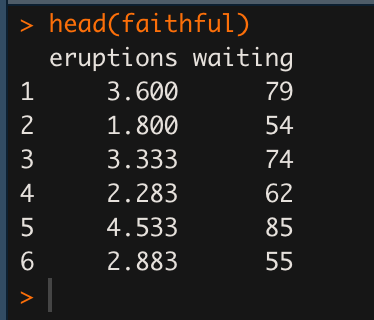
1
2
3
4
5
x <- faithful$eruptions
y <- faithful$waiting
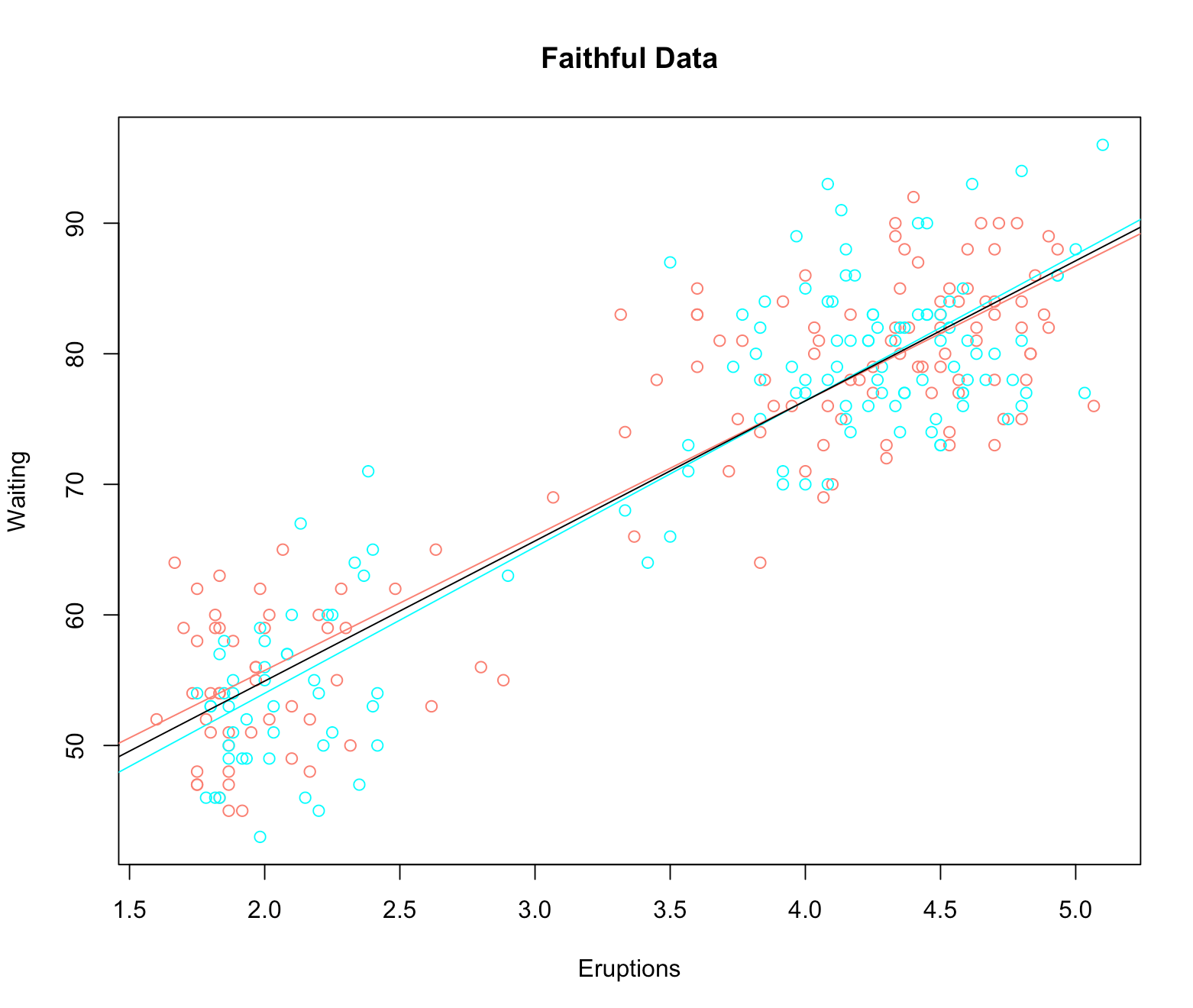
plot(x,y) # 선형 상관관계 있는 것으로 보인다.
cor(x,y) # 피어슨 상관계숫값 0.90 으로 높은 선형상관관계가 나타난다.
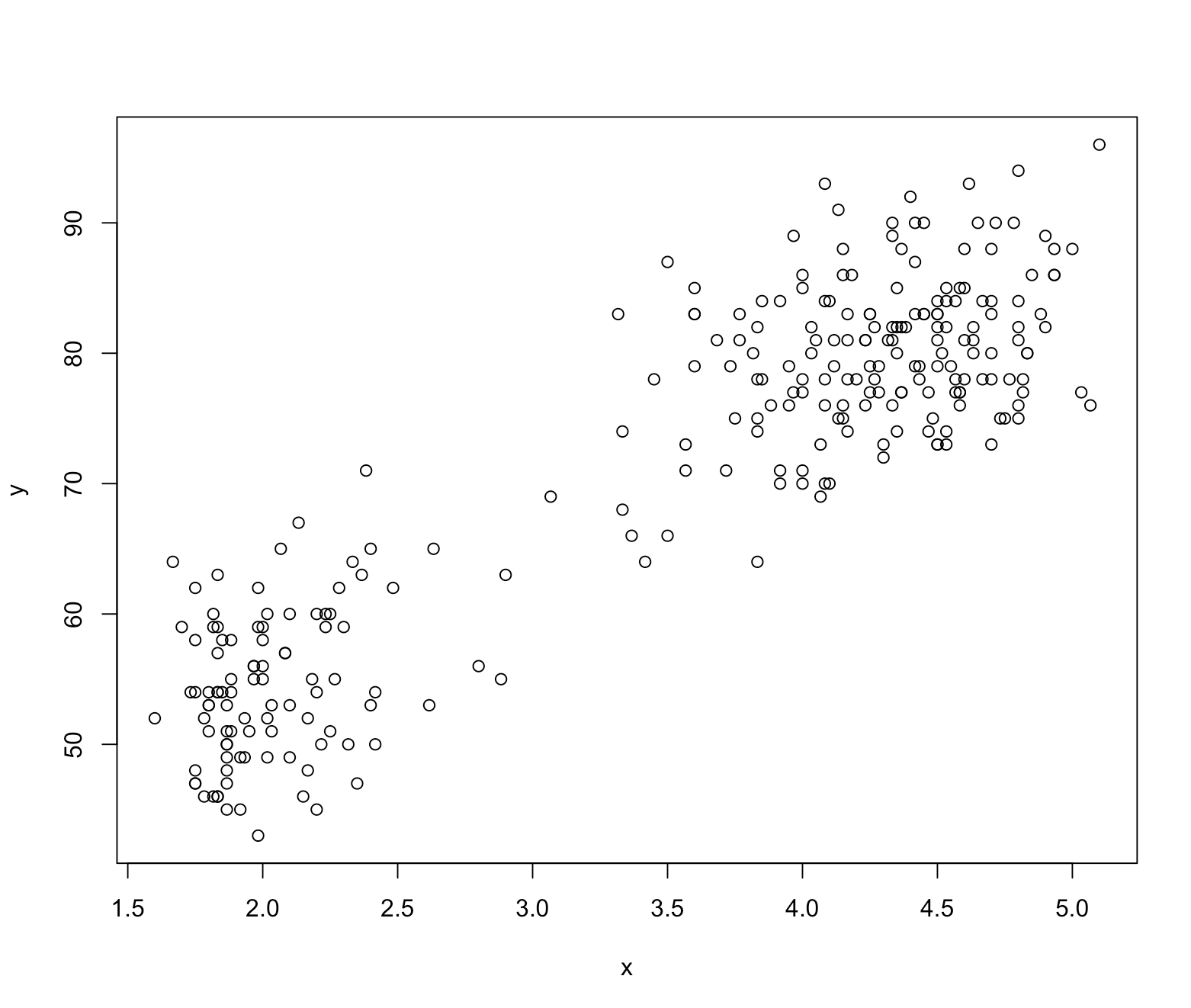
피어슨 상관계숫값: 0.90
1
2
3
# X축, Y축, 제목 라벨 부여하기
# x축, y축 값 제한 설정하기
plot(x,y, xlab='Eruptions', ylab='Waiting',main='Faithful Data',xlim = c(0,7), ylim=c(30,100))
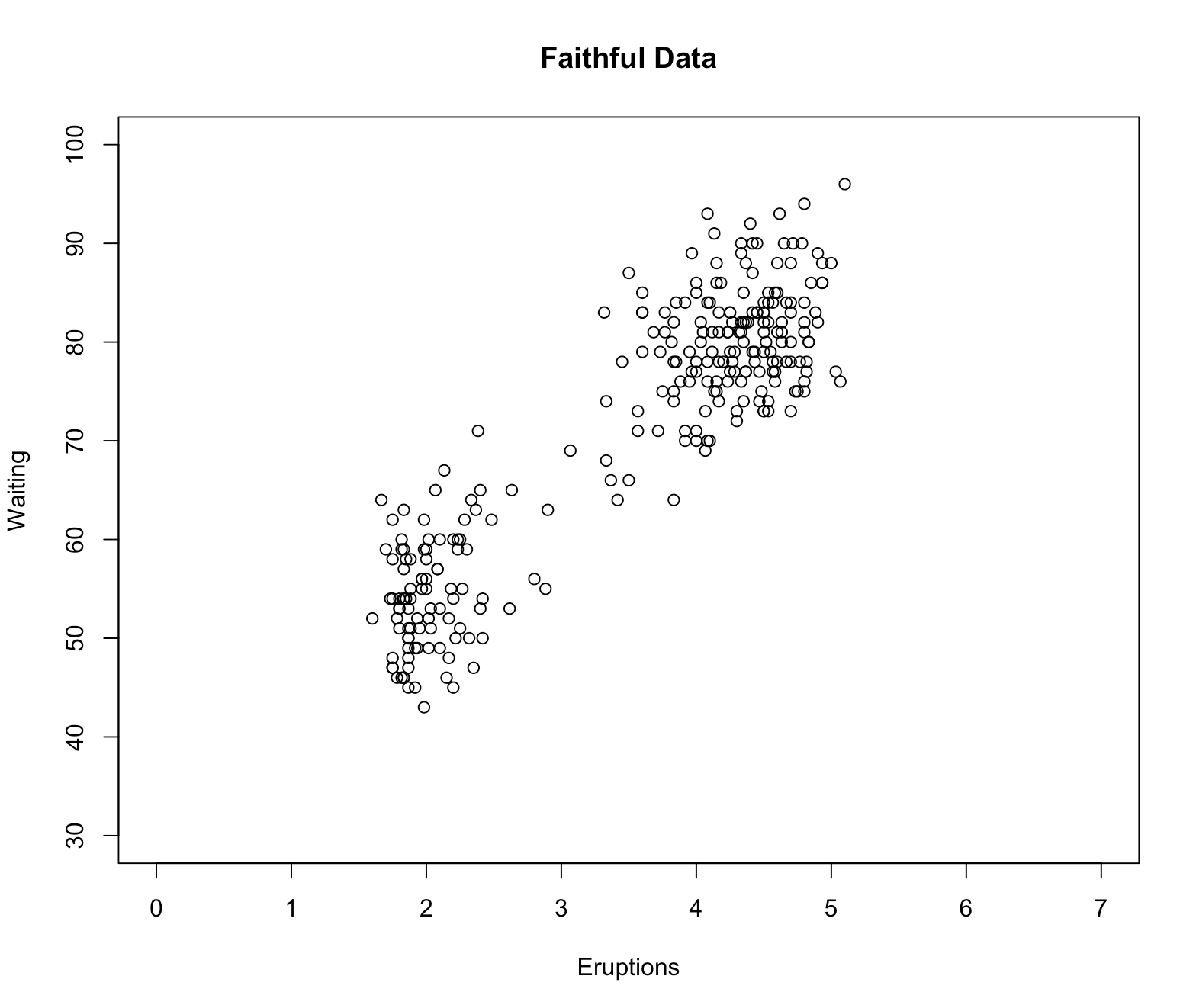
1
2
3
4
5
6
7
8
9
10
11
12
# 데이터 별로 구분해서 나타내기
x1 = x[1:136]
x2 <- x[137:272]
y1 <- y[1:136]
y2 <- y[137:272]
plot(c(x1, x2), c(y1, y2), type='n', xlab='Eruptions', ylab='Waiting', main='Faithful Data') # type='n'은 '점을 찍지 마라'는 명령이다.
points(x1, y1, col='salmon')
points(x2, y2, col='cyan')
abline(lm(y1~x1), col='salmon')
abline(lm(y2~x2), col='cyan')
abline(lm(y~x))