‘프로그래머가 알아야 할 알고리즘 40’(임란 아마드 지음, 길벗 출판사) 을 통해 선형회귀, 의사결정회귀나무, 의사결정회귀나무 앙상블을 공부하고 나서, 그 내용을 내 언어로 바꾸어 기록한다.
회귀문제
분류문제는 타겟값이 카테고리 확률변수였다.
$\Rightarrow$ 회귀문제는 타겟값이 연속확률변수다.
아래는 회귀문제 해결하는 데 사용할 수 있는, 회귀 알고리즘 들이다.
선형회귀 (Linear regression) 알고리즘
정의
여러 독립변수들과, 종속변수 사이 관계 선형으로 나타낸 것.
목표
현실에서 얻은 표본값들과 기댓값 예측치 사이 오차 가장 작게 하는, 독립변수 $i$ 의 가중치 $\beta_{i}$ 찾기.
종류
단순선형회귀
- 독립변수 1개와 종속변수 사이 관계 나타낸 것.
- $\hat{y} = \beta_{0} + \beta_{1}x_{1}$ or $y = \beta_{0} + \beta_{1}x_{1} + \epsilon$, $\epsilon$ 은 오차.
- $\beta_{0}$ 은 독립변수 가중치 $0$ 일 때 $\hat{y}$ 값
다중선형회귀
- 독립변수 $n$개와 종속변수 사이 관계 나타낸 것.
- $\hat{y} = \beta_{0} + \beta_{1}x_{1} + … + \beta_{n}x_{n}$ or $y = \beta_{0} + \beta_{1}x_{1} + … \beta_{n}x_{n} + \epsilon$, $\epsilon$ 은 오차.
- $\beta_{0}$ 은 독립변수 가중치 $0$ 일 때 $\hat{y}$ 값
선형회귀모델 예측값 $\hat{y}$ 의미
기댓값 예측치.
선형회귀모델 손실함수(RMSE)
Root Mean Squared Error.
오차제곱합에 루트 씌운 것. $\Rightarrow$ 모델의 전반적 오차.
$loss = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(\hat{y}^{i} - y^{i})^{2}}$
선형회귀모형으로 회귀문제 해결하기
데이터셋 로드
1
2
3
import pandas as pd
df = pd.read_csv('/Users/kibeomkim/Desktop/auto.csv') ; df
1
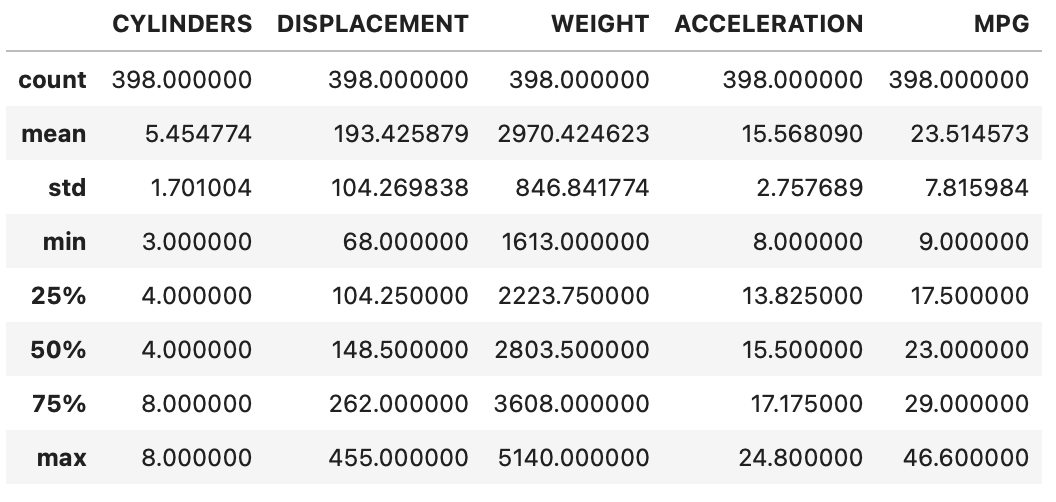
df.describe()
1
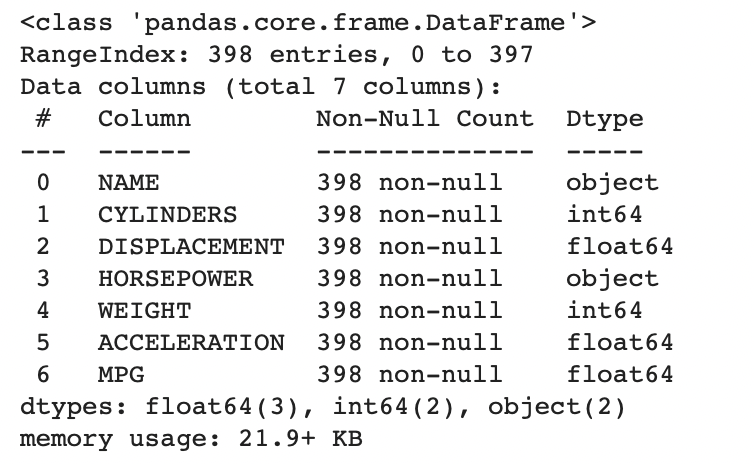
df.info()
1
df.isnull().sum()
데이터셋 전처리
1
2
3
4
5
6
7
# 데이터 파이프라인 정의
def pipeline(df) :
df.drop('NAME', axis=1, inplace=True)
df = df.apply(pd.to_numeric, errors='coerce')
df.fillna(0, inplace=True)
return df
df = pipeline(df)
훈련용 데이터셋과 테스트용 데이터셋으로, 전체 데이터셋 분리하기
1
2
3
4
5
6
7
8
9
10
# 전처리 후, 훈련셋과 검증셋으로 데이터셋 나누기
print(df.shape)
from sklearn.model_selection import train_test_split
# 타겟
y = df['MPG'].values
# 특성변수들
X = df.values
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=True)
선형회귀모델 훈련시키기
이 경우 여러 독립변수와 종속변수 1개 사용했으므로, 모델이 다중선형회귀모델이 된다.
1
2
3
4
5
6
# 선형회귀 모델 훈련시키기
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
# 회귀모델 훈련
regressor.fit(x_train, y_train)
모델 예측
1
2
3
4
5
6
y_pred = regressor.predict(x_test)
# Regressor 성능 평가 ; RMSE
from sklearn.metrics import mean_squared_error
from math import sqrt
print(sqrt(mean_squared_error(y_test, y_pred)))
RMSE value: 2.7248410669138417e-14
의사결정회귀나무
타겟값이 연속형이라는 것 제외하면, 의사결정나무(분류기)와 거의 같다.
- 기댓값 예측치 뽑아낸다.
의사결정회귀나무 모형으로 회귀문제 해결하기
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.tree import DecisionTreeRegressor
# 최대 깊이=3 인 의사결정 회귀나무 정의
regressor = DecisionTreeRegressor(max_depth=3)
# 모델 훈련
regressor.fit(x_train, y_train)
# 테스트 데이터에 대해 기댓값 근사치 예측 수행
y_pred = regressor.predict(x_test)
print(sqrt(mean_squared_error(y_test, y_pred)))
RMSE value: 1.4008722335107024
그레디언트 부스팅 알고리즘
경사하강으로 손실 계속 줄여가며 모델 (성능) 업데이트 하기.
앙상블에 계속 추가하는 개별 약 분류기로, 의사결정회귀나무 사용한다.
회귀문제 해결하기
1
2
3
4
5
6
7
from sklearn.ensemble import GradientBoostingRegressor
# 그레디언트 부스팅 회귀모델 정의
regressor = GradientBoostingRegressor(n_estimators=500, max_depth=4, min_samples_split=2, learning_rate=0.01, loss='ls')
# 회귀모델 훈련
regressor.fit(x_train, y_train)
GradientBoostingRegressor(learning_rate=0.01, loss=’ls’, max_depth=4, n_estimators=500)
1
2
3
4
5
6
# 테스트셋에 대해 예측
y_pred = regressor.predict(x_test)
# 회귀모델 성능
print(sqrt(mean_squared_error(y_test, y_pred)))
print('단일 의사결정 회귀나무 보다, 의사결정회귀나무 앙상블이 성능 더 좋았다 (1.4 > 0.265)')
RMSE value: 0.265994740897516
단일 의사결정 회귀나무 보다, 의사결정회귀나무 앙상블이 성능 더 좋았다 (1.4 > 0.265)
아래는 선형회귀모델, 단일 의사결정회귀나무, 의사결정회귀나무 앙상블(그래디언트 부스팅) 성능 비교 한 것이다.
1
2
3
4
5
result = pd.DataFrame({
'Algorithm' : ['Linear regression', 'Regression tree', 'Gradient Boosting'],
'RMSE' : [2.7404298600226993e-15, 1.4008722335107024, 0.265994740897516]
})
result
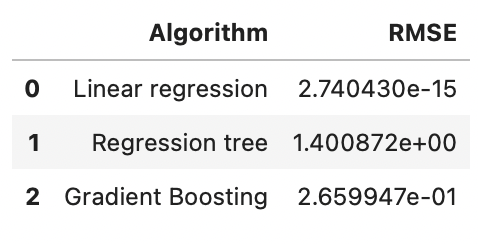
데이터프레임 시각화
1
2
3
4
plt.bar(range(len(result['RMSE'].values )), result['RMSE'].values )
plt.xticks(range(len(result['RMSE'].values)), result['Algorithm'].values)
plt.title('RMSE result')
plt.show()
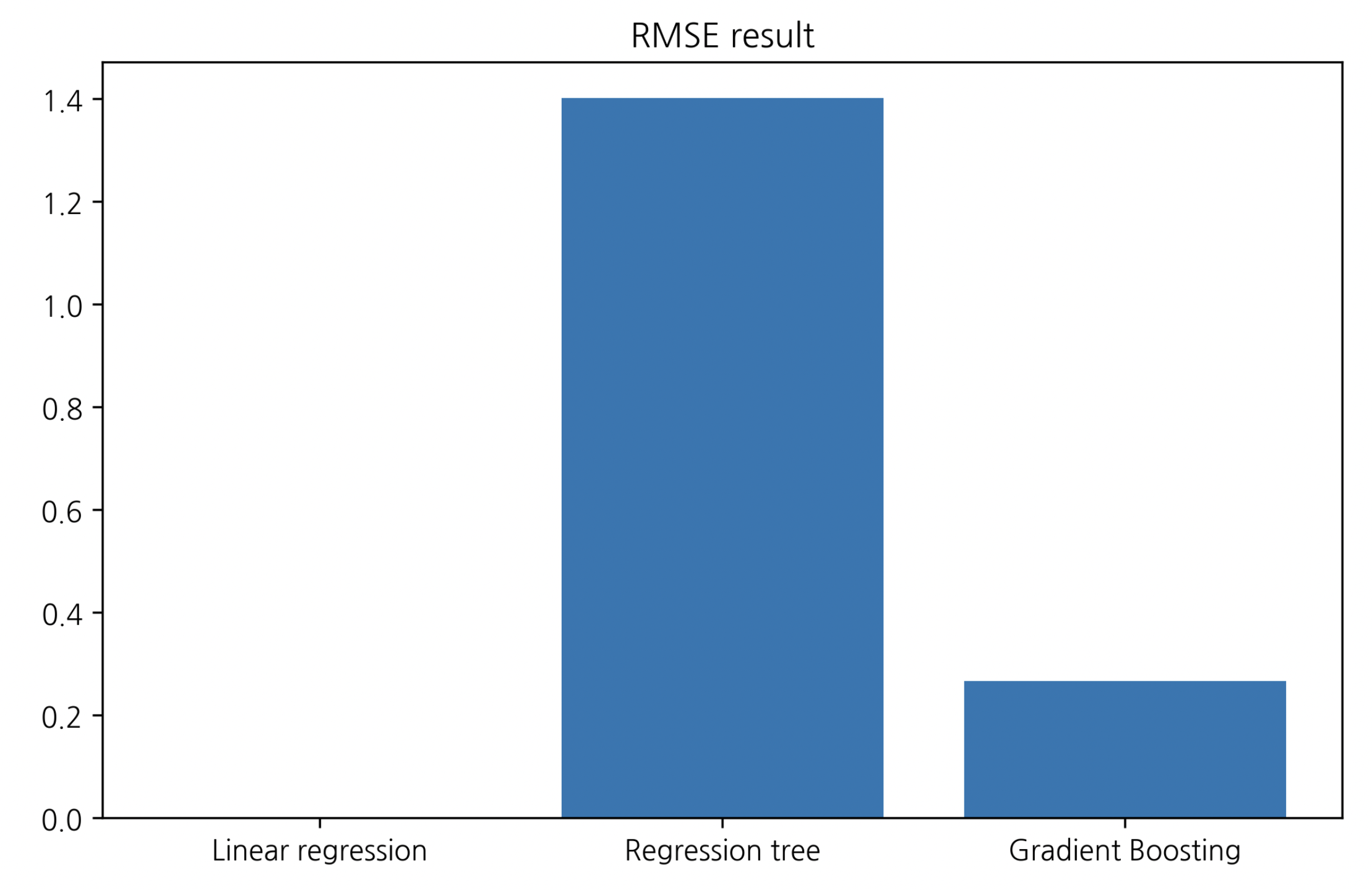
이 경우엔 선형회귀모델, 그레디언트 부스팅, 의사결정 회귀나무 순으로 성능 잘 나왔다.
