사이파이 사용해서 검정하기
- 파이썬 사이파이 패키지를 사용하면 다양한 검정을 쉽게 할 수 있다.
- 검정통계량 분포 그리고, 누적분포함숫값 직접 계산하고 안 해도 된단 거다.
요약
이항검정
검정통계량 분포로 이항분포 사용, 베르누이확률변수 모수가설 검정
카이제곱검정
카테고리분포 모수 $\mu$ 벡터 검정
카이제곱 독립검정
두 범주형 확률변수 사이 독립, 상관관계 유무 검정
단일표본 z 검정
정규분포 확률변수 기댓값 모수 $\mu$ 에 대한 가설 검정 ($\sigma^{2}$ 아는 경우)
단일표본 t 검정
정규분포 확률변수 기댓값 모수 $\mu$ 에 대한 가설 검정 ($\sigma^{2}$ 모르는 경우)
독립표본 t 검정
두 정규분포 기댓값 모수가 같은지 검정
대응표본 t 검정
1 : 1 대응되는 표본을 사용해서 독립표본 t 검정 시행
등분산 검정
두 정규분포 분산 모수 $\sigma^{2}$ 이 같은 지 검정
정규성 검정
표본분포가 정규분포 따르는 지 검정
KS 검정
두 표본분포가 같은 분포에서 나왔는 지 검정
정규성 검정에도 사용가능하다.
이항검정
- 검정할 확률변수 : 베르누이 확률변수
- 검정할 모수가설 : 모수 $\mu$ 에 대한 귀무가설
- 검정통계량 분포 : 이항분포
- 검정통계량 값 : N 번 중 성공 횟수 n 번 (이항분포 표본 1개)
이항검정 명령
1
scipy.stats.binom_test(x=, n=, p=, alternative=)
x : 검정통계량 값
n : N (총 시행 횟수)
p : 귀무가설 $H_{0}$ 의 모수
alternative : 양측검정이면 ‘two-sided’, 단측검정이면 ‘greater’, ‘less’
이항검정 실시 예)
데이터사이언스스쿨 - 9.5.3 연습문제
문) 어떤 주제에 대해 찬반을 묻는 설문조사를 실시했고, 설문조사 결과 응답자의 70% 가 찬성이라는 결과가 나왔다. 전체 국민의 2/3 가 넘게 찬성한다는 결론을 유의수준 1%에서 얻기 위해 필요한 응답자 수는 얼마인가?
단 응답자 수가 바뀌어도 찬성 70% 라는 결과는 바뀌지 않는다고 가정한다.
답)
문제의 정의 : n에 따른 유의확률을 구해야 한다. 유의확률값이 n이 얼마일 때 유의수준 1% 보다 작아지는 지 찾으면 된다.
확률변수 : ‘주제에 대한 찬반’ (베르누이확률변수)
시뮬레이션 : 설문조사
검정통계량값 : n * 0.7
검정통계량분포 : 이항분포
시뮬레이션으로 추정해낸 모수 $\mu$ : 0.7
모수추정 결과를 가지고 가설을 세워보자.
모수추정 결과를 보니 대략 $\frac{2}{3}$ 넘는 국민들이 주제에 대해 찬성할 것 같다.
저 모수추정 결과는 믿을만 한가?
= $\frac{2}{3}$ 넘는 국민이 주제에 찬성한다고 주장할 수 있는가?
내가 주장하고 싶은 바를 가지고 대립가설을 세우자.
$H_{a} : \mu$ > $\frac{2}{3}$
그러면 귀무가설은 다음과 같다.
$H_{0} : \mu = \frac{2}{3}$
귀무가설이 참인지, 거짓인지 증명하기 위해 사이파이 명령을 사용해 유의확률을 구해보자.
일정 범위 n 값을 주고, n별 유의확률 값을 그래프로 그린다.
n이 얼마일 때 0.01 선 밑으로 내려가는지(작아지는지) 보면 될 것이다.
1
2
3
4
5
6
7
8
9
10
# 9.5.3 연습문제
nn = np.arange(0,2001)
p_values = [sp.stats.binom_test(int(np.round(n*0.7)), n=n, p=2/3, alternative='greater') for n in nn]
plt.plot(nn, p_values, 'ro-')
plt.hlines(0.01, xmin=0, xmax=2000, colors='g', ls=':')
plt.ylim(0.004,0.0125)
plt.xlim(1110, 1140)
plt.title('1116명 이상일 때 항상 대립가설 채택')
plt.show()

1116명 이상일 때 그래프가 처음으로 0.01 선 밑으로 내려간다.
곧, 1116명 이상 설문 응답자를 모으면 이들로부터 얻은 유의확률이 0.01보다 작아져서, 귀무가설을 기각할 수 있게 된다는 뜻이다.
귀무가설을 기각하고 대립가설을 채택한다. 따라서 1116명 이상일 때 “ $\frac{2}{3}$ 넘는 국민들이 주제에 대해 찬성한다 “ 고 주장할 수 있다.
카이제곱검정 (=적합도검정)
- 검정 할 확률변수 : 카테고리확률변수
- 검정 할 모수가설 : 모수 $\mu$ 벡터에 대한 가설 검정
- 검정통계량 : 다항분포 표본 1개를 [이용해서] 검정통계량 값 계산
$t = \sum_{k=1}^{k} \frac{(x_{k}-m_{k})^{2}}{m_{k}}$
카이제곱검정 명령
1
sp.stats.chisquare(다항분포표본 1개, 귀무가설 mu 벡터 값)
카이제곱검정 시행 예)
사면체 주사위를 100번 던졌다.
1은 37번, 2는 32번, 3은 20번, 4는 11번 나왔다.
이 주사위는 공정한 주사위인가?
답)
확률변수 : 사면체 주사위 (카테고리확률변수)
시행횟수N : 100
검정통계량 값 : 다항분포 표본 1개 이용해서 구하자
카테고리확률변수는 원핫인코딩벡터 꼴 표본을 내놓는다.
$[0,0,0,1]$ 이런 식이다.
이 표본들을 이용해서 카테고리확률변수 시뮬레이션 100번 했을 때의 다항분포 표본 1개를 얻자.
$1 = [1,0,0,0]$
$2 = [0,1,0,0]$
$3 = [0,0,1,0]$
$4 = [0,0,0,1]$
1이 37번 / 2가 32번 / 3이 20번 / 4가 11번
원핫인코딩 벡터 합으로 위 결과 나타내면
$[37, 32, 20, 11]$ 이다.
이 다항분포 표본 1개 이용해서 검정통계량 값 구한다.
한편 나는 이 주사위 나온 결과를 보니 주사위가 불공정한 주사위 같다(모수 벡터 $\mu$ 값이 불균등하게 분배되어 있다)
따라서 나는 ‘이 주사위는 불공정한 주사위다’를 증명해 보이고 싶다.
여기 따라 대립가설을 놓는다.
$H_{a} : \mu \ne [0.25, 0.25, 0.25, 0.25]$
그러면 귀무가설은 다음과 같다.
$H_{0} : \mu = [0.25, 0.25, 0.25, 0.25]$
이제 카이제곱검정을 실행해서 유의확률을 구해보자.
1
2
3
4
5
6
7
8
9
10
11
n = 100
k = 4
np.random.seed(0)
mu0 = np.array([0.35, 0.3, 0.2, 0.15])
x = np.random.choice(k, n, p=mu0)
result = np.bincount(x, minlength = k)
sp.stats.chisquare(result, np.array([0.25, 0.25, 0.25, 0.25]))
Power_divergenceResult(statistic=16.56, pvalue=0.0008703471978912127)
유의확률값이 0.08% 이다. 귀무가설 기각할 수 있다. 대립가설 채택하면, “이 주사위는 공정하지 못한 주사위다”라고 주장할 수 있다.
$\mu \ne [0.25, 0.25, 0.25,0.25]$
카이제곱 독립검정
- 검정 할 확률변수 : 두 범주형 확률변수 $X$, $Y$
- 검정 내용 : 두 범주형 확률변수가 독립인가? 상관관계가 있나?
$H_{0} : \mu_{1} = \mu_{2}$
$H_{a} : \mu_{1} \ne \mu_{2}$
- 위 가설에서 $\mu_{1}$ 과 $\mu_{2}$ 는 두 조건부확률분포 $P(Y\vert{X=0})$ 과 $P(Y\vert{X=1})$ 의 기댓값 모수 $\mu_{1}, \mu_{2}$ 라고 보면 된다. 확률변수 $X$ 와 $Y$가 서로 독립이라면 $Y$가 $X$에 영향 받지 않기 때문에 두 확률분포는 ‘같을 것이다’. 그게 귀무가설로 표현된 것이다. 한편, 두 확률변수가 서로 상관관계가 있다면 두 조건부확률분포는 서로 ‘다를 것이다’. 그게 대립가설로 표현된 것이다.
귀무가설 채택 : X,Y 확률변수 서로 상관관계 없다. 서로 독립이다.
대립가설 채택 : X,Y 확률변수 서로 상관관계 있다.
카이제곱 독립검정 명령
1
sp.stats.chi2_contingency(x)
x : X, Y 확률변수 결합확률분포 표본 갯수 표
예 )
1
2
3
4
x = np.array([
[2,3],
[8,9]
])
카이제곱 독립검정 시행 예)
데이터사이언스스쿨 연습문제 9.5.5
문 ) 데이터사이언스스쿨 수업을 들었는가 여부가 나중에 대학원에서 머신러닝 수업의 학점과 상관관계가 있는지 알기 위해 데이터를 구한 결과가 다음과 같다고 하자.
데이터사이언스 스쿨 수업 듣지 않은 경우 즉 X가 0 이면 A,B,C 학점(Y값) 을 받은 학생의 분포가 4,16,20 이다.
데이터사이언스 스쿨 수업 들은 사람의 경우 즉, X가 1일 때 A,B,C학점(Y값)을 받은 학생 분포가 23, 18, 19다.
이 결과로부터 ‘데이터사이언스스쿨 수업 들었는가 여부’가 ‘머신러닝 수업 학점’과 상관관계가 있다고 말할 수 있는가?
답 )
데이터사이언스스쿨수업 들었는가 여부 : 베르누이확률변수 X
머신러닝수업 학점 : 카테고리확률변수 Y
문제 : 두 확률변수 사이 상관관계가 있다고 할 수 있는가?
X,Y 확률변수는 모두 범주형 확률변수다. 두 범주형 확률변수 사이 독립인지, 상관관계있는지 알기 위해 카이제곱 독립검정을 쓰자.
결합확률분포 표본갯수 표 :
1
2
3
4
5
# 연습문제 9.5.5
x = np.array([
[4,6,20],
[23,18,19]
])
카이제곱 독립검정 명령
1
2
3
4
result = sp.stats.chi2_contingency(x)[1]
print(f'유의확률 : {result}')
print(f'귀무가설 기각, 대립가설 채택')
print(f'베르누이확률변수와 카테고리확률변수 간 상관관계가 있다고 말할 수 있다')
유의확률 : 0.00704786570249751
귀무가설 기각, 대립가설 채택
베르누이확률변수와 카테고리확률변수 간 상관관계가 있다고 말할 수 있다
곧, ‘데이터사이언스스쿨 수업을 들었는가 여부’와 ‘머신러닝 수업 학점’ 간 ‘상관관계’가 있다고 말할 수 있다.
단일표본 Z 검정
- 검정 할 확률변수 : 분산모수 $\sigma^{2}$ 을 아는 정규분포 확률변수
- 검정 할 모수가설 : 정규분포 기댓값 모수 $\mu$ 에 대한 가설
- 검정통계량 값 : Z 통계량값
- 검정통계량 분포 : 표준정규분포
사이파이 패키지가 따로 없다. 누적분포함수 이용해서 직접 계산하자.
예)
정규분포 분산값 $\sigma^{2} = 1$ 인 정규분포에서 데이터 100개를 얻어 단일표본 Z검정을 해보자.
귀무가설은
$H_{0} : \mu = 0$
대립가설은
$H_{a} : \mu \ne 0$ 으로 임의 설정했다.
참고로 데이터를 얻는 정규분포의 실제 기댓값 모수는 $\mu = 0$ 이다.
가설검정 결과가 위 실젯값대로 정확하게 나오는지 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
N = 100
mu0 = 0
sigma2 = 1
rv = sp.stats.norm(loc=mu0, scale=1).rvs(N, random_state=0)
def z_test(rv, sigma2, N) :
z = np.mean(rv)/sigma2*np.sqrt(N)
if z >= 0 :
p_value = (1-sp.stats.norm().cdf(z))*2
elif z < 0 :
p_value = sp.stats.norm().cdf(z)*2
return z, p_value
result = z_test(rv, sigma2, N)[1]
print(f'유의확률 : {result}')
print(f'귀무가설 채택')
유의확률 : 0.5497864508624168
귀무가설 채택한다. 곧, 실젯값 대로 귀무가설이 참이라고 판명되었다.
단일표본 t 검정
검정 할 확률변수 : 분산 $\sigma^{2}$ 값을 모르는 정규분포 확률변수
검정 할 모수가설 : 정규분포 기댓값 모수 $\mu$ 에 대한 가설 검정
검정통계량 값 : t 통게량 값
검정통계량 분포 : 자유도 N-1 인 스튜던트 t분포
단일표본 t 검정 명령
1
sp.stats.ttest_1samp(a, popmean)
a : 정규분포 표본 데이터들 배열
popmean : 귀무가설 모수 $\mu$
예)
정규분포에서 나온 데이터 100개를 가지고 있다.
귀무가설이
$H_{0} : \mu = 0$
대립가설이
$H_{a} : \mu \ne 0$
일 때, 가설검정을 해보자.
참고로 표본을 뽑아낸 원래 정규분포 기댓값 모수는 0 이었다.
1
2
3
4
5
6
N = 100
mu0 = 0
rv = sp.stats.norm().rvs(N, random_state=0)
sp.stats.ttest_1samp(rv, popmean=mu0)
Ttest_1sampResult(statistic=0.5904283402851698,
pvalue=0.5562489158694675)
유의확률이 55%로, 유의수준보다 크다. 따라서 귀무가설 채택한다.
$H_{0} : \mu = 0$
독립표본 t 검정
- 검정 내용 : 두 정규분포의 기댓값이 같은지 검정
- 두 정규분포는 서로 독립
$H_{0} : \mu_{1} = \mu_{2}$
$H_{a} : \mu_{1} \ne \mu_{2}$
검정통계량분포 : 스튜던트 t분포
검정통계량 값 : 분산값이 같으냐, 다르냐에 따라 사용하는 검정통계량 값이 다르다.
독립표본 t 검정 명령
1
2
sp.stats.ttest_ind(a,b, equal_var=True)
a : 1번 표본 집합 데이터
b : 2번 표본 집합 데이터
equal_var : 두 정규분포 분산값 같은지 여부. 같으면 True 아니면 False.
- 양측검정이다.
예)
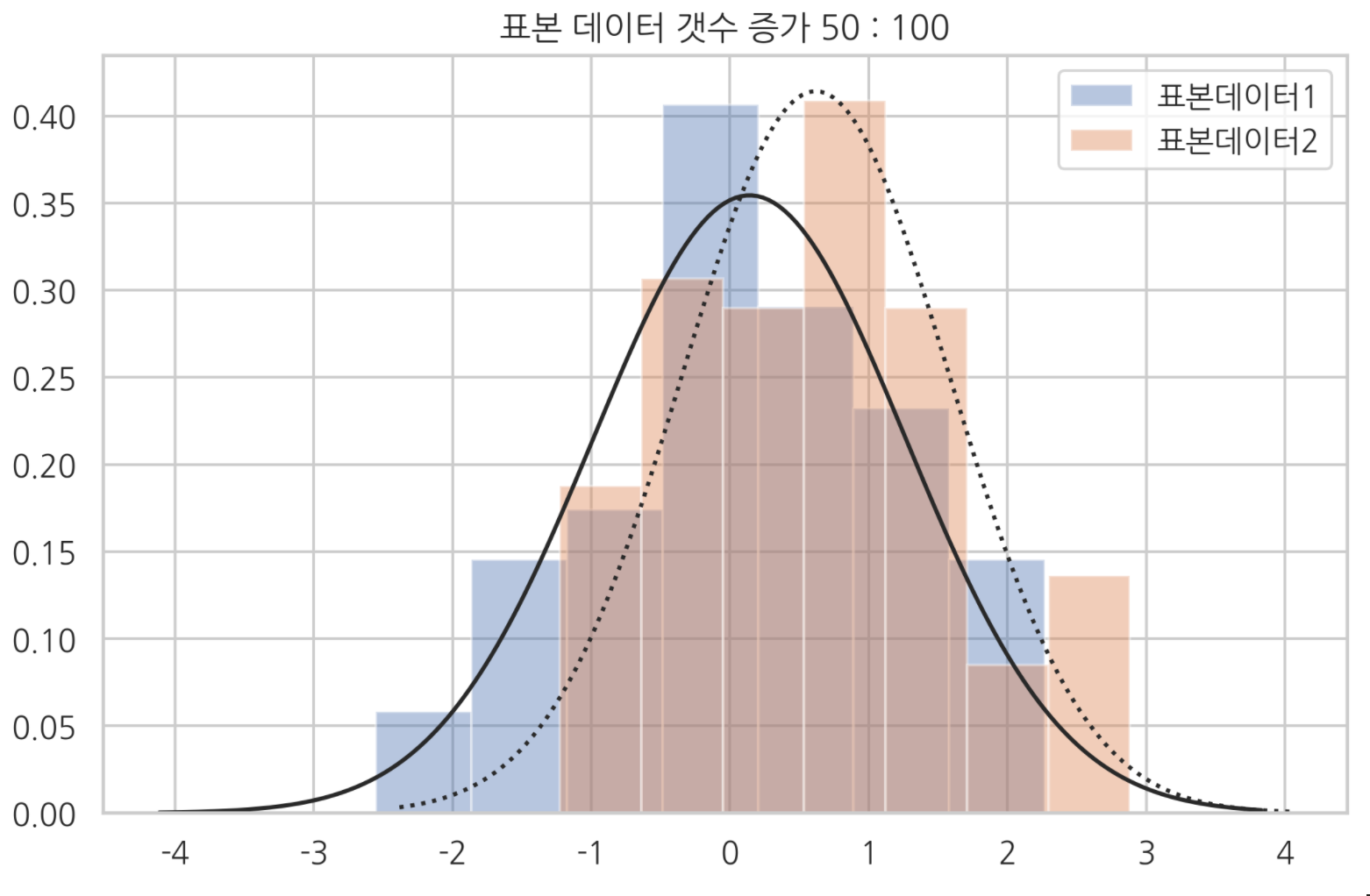
서로 독립인 두 정규분포에서 표본데이터 집합 1,2 를 얻자.
이 두 집합으로 독립표본 t 검정 실시해서, 두 정규분포 기댓값이 같은지 검정하자.
참고로 두 표본데이터 집단을 얻는 정규분포의 원래 기댓값은 $\mu_{1} = 0, \mu_{2} = 0.5$로 다르고 분산은 $\sigma_{1}=\sigma_{2}=1$ 로 같으며 표본 수가 $N_{1}=50, N_{2}=100$ 개다.
검정 결과가 실재를 잘 반영하는지도 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
n1 = 50
mu1 = 0
sigma21 = 1
n2 = 100
mu2 = 0.5
sigma22 = 1
np.random.seed(0)
x1 = sp.stats.norm(loc=mu1, scale=sigma21).rvs(n1)
x2 = sp.stats.norm(loc=mu2, scale=sigma22).rvs(n2)
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label='표본데이터1')
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label='표본데이터2')
ax.lines[1].set_linestyle(':')
plt.legend()
plt.title('표본 데이터 갯수 증가 50 : 100')
plt.show()
1
np.mean(x1), np.mean(x2)
두 표본데이터집단 각 표본평균 : (0.14055927231309787, 0.6177957994523524)
큰수의 법칙에 따라 표본평균은 모집단 평균의 근삿값이다.
표본평균값을 계산해서 비교해 보았을 때, 두 값이 달랐다.
이를 통해 두 표본데이터 집단이 나온 두 정규분포 모수도 다를 것이라고 추정할 수 있다.
이 내용을 대립가설로 놓는다.
$H_{a} : \mu_{1} \ne \mu_{2}$
그러면 귀무가설은 다음과 같다.
$H_{0} : \mu_{1} = \mu_{2}$
이제 두 표본 데이터 집단 1,2 를 이용해서 귀무가설이 참인지, 거짓인지 보자.
두 정규분포의 기댓값 모수가 같은지 다른지 검정하기 위해서는 독립표본 t 검정을 실시해야 한다.
1
sp.stats.ttest_ind(x1, x2, equal_var=False)
Ttest_indResult(statistic=-2.5427747064864556,
pvalue=0.012800307550312669)
유의확률 값이 0.0128이다.
5% 유의수준에서 귀무가설 기각 가능하다. 대립가설 채택.
$H_{a} : \mu_{1} \ne \mu_{2}$
“두 정규분포 기댓값이 다르다” 고 주장할 수 있다.
처음에 데이터가 나온 정규분포의 실제 기댓값이 다르다는 걸 생각했을 때, 실재를 잘 반영한 검정결과라고 볼 수 있다.
대응표본 t 검정
- 검정내용 : 1 : 1 대응되는 표본들로 독립표본 t 검정 수행
(두 정규분포 기댓값이 같은지 검정)
$H_{0} : \mu_{1} = \mu_{2}$
$H_{a} : \mu_{1} \ne \mu_{2}$
- 검정통계량값 : t통계량
- 검정통계량 분포 : t분포
- 분산이 같은지 다른지는 신경쓰지 않는다.
- 장점 : 적은 데이터로도 독립표본 t검정을 오류없이 수행할 수 있다.
대응표본 t 검정 명령
1
sp.stats.ttest_rel(a,b)
a : 1번 표본데이터 집합
b : 2번 표본데이터 집합
- 양측검정이다.
등분산검정
- 검정내용 : 두 정규분포 분산이 같은 지 검정
$H_{0} : \sigma_{1}^{2} = \sigma_{2}^{2}$
$H_{a} : \sigma_{1}^{2} \ne \sigma_{2}^{2}$
- 독립표본 t검정 할 때 선행해야 한다.
독립표본 t검정에서는 두 정규분포 분산이 같은지 다른지에 따라 검정통계량 값이 달라졌다.
따라서 독립표본 t검정 하기 전에는 두 정규분포 분산이 같은지 다른지 확인해야 한다.
이때 등분산검정을 활용할 수 있다.
- 종류 : 바틀렛(bartlett), 플리그너(fligner), 레빈(levene)
등분산검정 종류에 따라 검정 결과도 다르다.
등분산검정 명령
바틀렛 검정
1
sp.stats.bartlett(x1, x2)
플리그너 검정
1
sp.stats.fligner(x1, x2)
레빈 검정
1
sp.stats.levene(x1, x2)
예)
실제로 분산이 다른 두 정규분포에서 표본데이터 집합 얻자.
두 표본데이터 집합 이용해서 두 정규분포 분산이 같은지, 다른지 검정해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n1 = 800
n2 = 700
sigma1 = 1
sigma2 = 1.2
np.random.seed(0)
x1 = sp.stats.norm(3, sigma1).rvs(n1)
x2 = sp.stats.norm(5, sigma2).rvs(n2)
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label='1번 표본')
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label='2번 표본')
ax.lines[1].set_linestyle(':')
plt.legend()
plt.title('표본데이터 1, 2')
plt.show()

두 표본데이터 집합을 얻었다.
비편향표본분산은 모분산의 근삿값이었다.
두 데이터집단의 비편향표본분산값을 구해서, 모분산이 같을지 다를지 추정해보자.
1
2
print(x1.var(ddof=1), x2.var(ddof=1))
print(f'분산모수 다를 것 같다')
비편향표본분산값 :
x1 : 0.9941394887614771
x2 : 1.3240342982563584
두 모집단 분산모수 값이 다를 것 같다.
그러면 대립가설을 다음과 같이 세울 수 있다.
$H_{a} : \sigma_{1}^{2} \ne \sigma_{2}^{2}$
귀무가설은 다음과 같아진다.
$H_{0} : \sigma_{1}^{2} = \sigma_{2}^{2}$
귀무가설이 참인지, 거짓인지 등분산검정으로 검정해보자.
바틀렛 검정
1
sp.stats.bartlett(x1, x2)
BartlettResult(
statistic=15.343053846339838,
pvalue=8.964992621009065e-05)
플리그너 검정
1
sp.stats.fligner(x1, x2)
FlignerResult(
statistic=11.821107559476658,
pvalue=0.0005856301367977482)
레빈 검정
1
sp.stats.levene(x1, x2)
LeveneResult(
statistic=12.256042270504519,
pvalue=0.00047735588309963205)
세 등분산검정 모두 귀무가설 기각, 대립가설 채택 결과가 나왔다.
따라서
$H_{a} : \sigma_{1}^{2} \ne \sigma_{2}^{2}$
이다. 두 정규분포 분산이 다르다고 주장할 수 있다.
정규성검정
- 검정내용 : 표본분포가 정규분포 따르는지 검정한다.
$H_{0} :$ 표본분포가 정규분포 따른다
$H_{a} :$ 표본분포가 정규분포 따르지 않는다.
- 정규성검정은 여러 종류가 많다.
예)
사이파이
- 샤피로-윌크 검정
1
sp.stats.shapiro(x)
x : 표본데이터 집단
- 다고스티노 K-제곱 검정
1
sp.stats.mstats.normaltest(x)
x : 표본데이터 집단
스탯츠모델스
- 콜모고로프-스미르노프 검정
1
statsmodels.stats.diagnostic.kstest_normal(x)
x : 표본데이터 집단
- 옴니버스 검정
1
statsmodels.stats.diagnostic.omni_normtest(x)
x : 표본데이터 집단
KS 검정
콜모고로프-스미르노프 검정
- 두 표본분포가 같은 분포에서 나왔는지 검정
$H_{0} : \theta_{1} = \theta_{2}$
$H_{a} : \theta_{1} \ne \theta_{2}$
- 정규성검정에도 사용할 수 있다.
예)
실제로 다른 분포에서 나온 두 표본분포를 가지고 KS 검정을 해보자.
1
2
3
4
5
6
7
8
9
10
11
n1 = 200
n2 = 50
np.random.seed(0)
x1 = sp.stats.norm(1,3).rvs(n1)
x2 = sp.stats.norm(4,6).rvs(n2)
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label='1번 데이터 집합')
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label='2번 데이터 집합')
plt.legend()
plt.show()
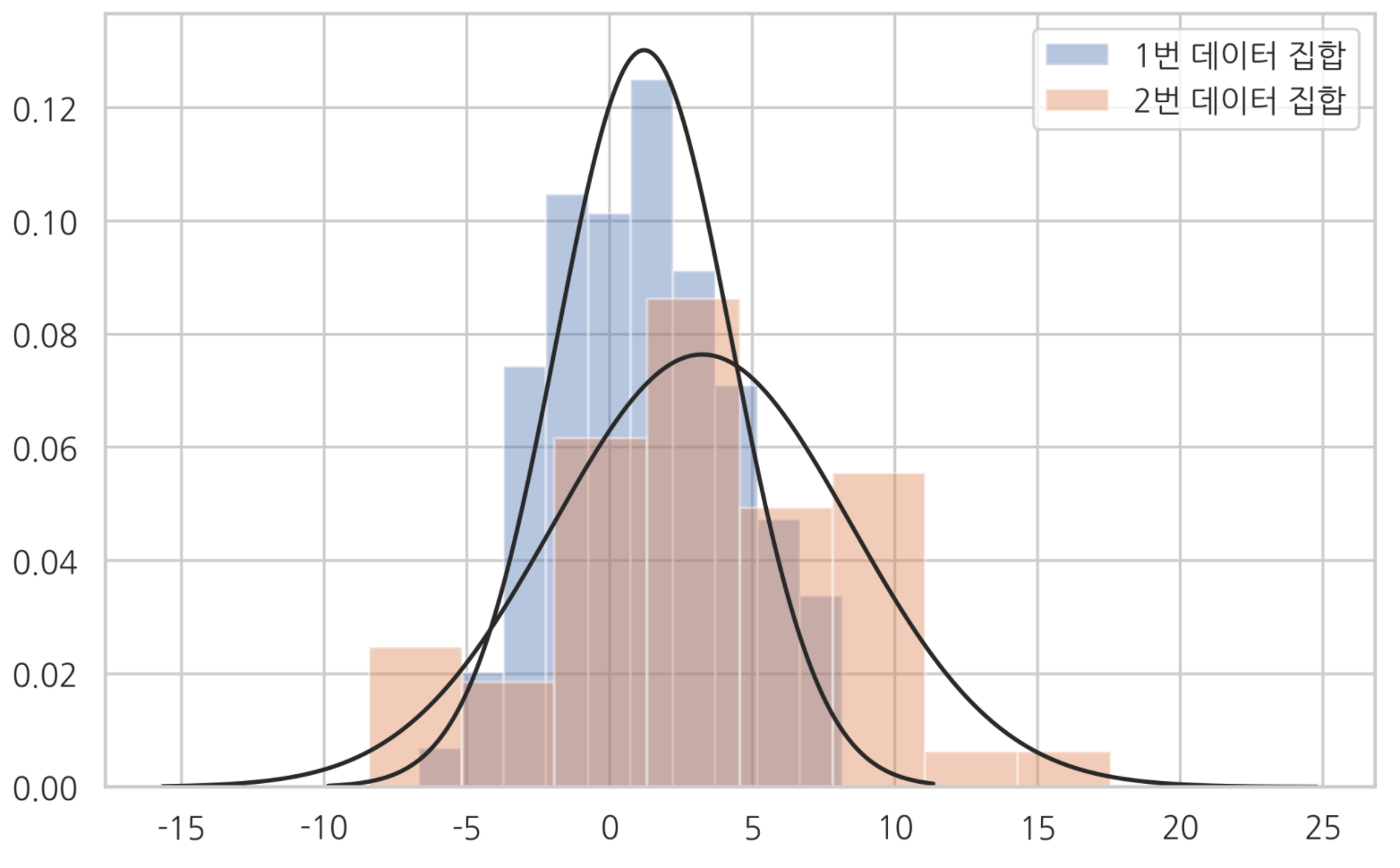
두 표본데이터를 얻었다. 두 표본데이터가 어떤 분포에서 나왔을 지 추정해보니 다른 분포에서 나온 것 같다.
‘두 분포가 다른 분포에서 나왔다!’ 고 주장하려면 대립가설은 다음처럼 세울 수 있다.
$H_{a} : \theta_{1} \ne \theta_{2}$
그러면 귀무가설은 다음과 같다.
$H_{0} : \theta_{1} = \theta_{2}$
두 표본분포가 같은 분포에서 나왔는지 검정하기 위해 KS검정을 사용하자.
1
sp.stats.ks_2samp(x1, x2)
KstestResult(
statistic=0.255,
pvalue=0.009610378185668456)
유의확률이 1%, 5%, 10% 유의수준보다 모두 작으므로, 귀무가설 기각할 수 있다. 곧, ‘두 분포가 다른 분포에서 나왔다’ 고 주장할 수 있다.
$H_{a} : \theta_{1} \ne \theta_{2}$
KS검정은
정규성검정에도 활용할 수 있다.
균등분포에서 표본데이터 10개를 얻었다.
이 표본데이터 집단이 특정 정규분포에서 나온 분포인지 알고싶다고 하자.
이때, 이 표본데이터 집단을 특정정규분포에서 나온 표본집단과 KS검정 하면 이 데이터들이 그 정규분포에서 나왔는지 알 수 있다.
1
2
3
4
5
x1 = sp.stats.uniform().rvs(10, random_state=0)
rv = sp.stats.norm(1,2).rvs(10000, random_state=0) # 기댓값이 1, 표준편차가 2인 정규분포에서 나온 표본 1만 개
sp.stats.ks_2samp(x1, rv)
KstestResult(
statistic=0.4972
pvalue=0.008347274897892887)
KS 검정결과 유의확률이 0.8% 로, 귀무가설 기각할 수 있다.
곧, ‘두 분포가 서로 다른 분포에서 나왔다’는 대립가설이 채택된다.
결과로, 내가 얻은 표본데이터 집단 x1이 평균1, 표준편차 2인 정규분포를 따르지 않음을 알 수 있다.
검정결과 오류(1, 2종 오류)
1종오류 : 귀무가설이 원래 참인데 거짓이라고 기각되는 경우 발생
2종오류 : 귀무가설이 원래 거짓인데 참이라고 채택되는 경우 발생
데이터 수가 부족하면 1,2종 오류가 잘 발생한다.
데이터를 더 모으면 1,2종 오류가 사라지거나, 덜 발생한다
