선형대수와 해석기하의 기초
선형대수 : 선과 도형, 수와 수의 관계를 다루는 학문
n차원 벡터의 기하학적 의미
- n차원 벡터 공간 상의 ‘점’
- n차원 벡터 공간의 원점과 점을 연결한 화살표
화살표로서의 벡터는 크기와 방향 두 가지를 표현한 것이다.
벡터를 화살표로 생각할 경우, 길이와 방향을 고정한 채 화살표만 평행이동 해도 상관없다(= 같은 벡터다)
벡터의 길이
- 벡터의 길이(크기)는 norm놈 값으로 나타낸다.
$\lVert a \rVert =\sqrt{a^{T}a}$
벡터 요소 제곱합에 루트 씌운 것.
1
2
3
#벡터 놈
a = np.array([0.5, 0.3, 0.1, 0.2])
np.linalg.norm(a) # 놈 계산
스칼라와 벡터 곱
- 벡터에 양의 실수(스칼라)를 곱하면 방향은 안 변하고 벡터 길이만 변한다.
- 벡터에 음의 실수(스칼라)를 곱하면 방향이 반대로 바뀌고 벡터 길이가 변한다.
단위벡터
- 벡터 길이(놈 값이)가 1인 벡터
$norm(a) = 1$
영벡터 아닌 임의의 벡터에 대해 다음처럼 하면 원래 벡터와 방향은 같지만 길이가 1인 단위벡터가 된다.
$\frac{x}{\lVert x \rVert}$
벡터 합
- 벡터 합은 차원이 같은 벡터끼리 할 수 있다. 결과도 벡터다.
- 기하학적 관점에서 벡터 합은 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
plt.ylim(-1,1)
plt.xlim(-1,2)
black = {'facecolor' : 'black'}
blue = {'facecolor' : 'blue'}
plt.annotate('', xy=[1,0], xytext=[0,0], arrowprops=black)
plt.annotate('', xy=[2/5, -1/2], xytext=[0,0], arrowprops=black)
plt.annotate('', xy=[3/5,1/2], xytext=[0,0], arrowprops=black)
plt.annotate('', xy=[1,0], xytext=[3/5, 1/2], arrowprops=blue)
plt.scatter(1,0, 100, 'r')
plt.text(0.1, -0.28, 'a')
plt.text(0.19, 0.3, 'b')
plt.text(0.6, 0.1, 'c')
plt.show()

a 벡터와 b 벡터 합은 c벡터로, 위 그림과 같다.
a 벡터를 더하고자 하는 b 벡터 점으로 평행이동 시켰을 때, 평행이동한 a벡터(파란색 화살표) 가 가리키는 점이 a+b 벡터(c벡터)이다.
벡터 차
- 기하학적 관점에서 벡터 차는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 벡터 차
plt.ylim(-1,1)
plt.xlim(-1,2)
black = {'facecolor' : 'black'}
blue = {'facecolor' : 'blue'}
plt.annotate('', xy=[2/5, -1/2], xytext=[0,0], arrowprops=black)
plt.annotate('', xy=[3/5,1/2], xytext=[0,0], arrowprops=black)
plt.annotate('', xy=[2/5, -1/2], xytext=[3/5, 1/2], arrowprops=blue)
plt.text(0.1, -0.28, 'a')
plt.text(0.19, 0.3, 'b')
plt.text(0.6, 0.0, 'a-b')
plt.scatter(2/5, -1/2, 100, 'r')
plt.scatter(3/5,1/2, 100, 'r')
plt.show()

a-b를 계산한다고 치자.
b벡터가 가리키는 점에서 a벡터가 가리키는 점으로 화살표를 연결하면, 그 벡터가 a-b 벡터(파란색 화살표)가 된다.
유클리드 거리
- a,b 두 벡터가 있다고 할 때, 두 벡터가 가리키는 점과 점 사이 거리
$\rVert a-b \lVert^{2} = \rVert a \lVert^{2} + \rVert b \lVert^{2} - 2a^{T}b$
- 유사도 구하려는 두 벡터 길이가 비슷비슷 할 때, 유클리드 거리는 코사인유사도와 비슷하게 쓸 수 있다.
벡터 내적 $a^{T}b$ 가 $\rVert a \lVert \rVert b \lVert cos\theta$ 와 같기 때문이다.
벡터 a,b 길이가 모두 비슷하다면 결국 유클리드거리 제곱 값을 결정짓는건 벡터 간의 코사인 유사도 값이다.
따라서 두 벡터 길이가 비슷할 때, 유클리드 거리를 코사인 유사도 처럼 사용할 수 있다.
한편, 유클리드거리를 이용하면 고차원벡터의 저차원 투영성분이 여러 저차원벡터 중 원래 벡터와 가장 비슷한 벡터라는 사실을 알 수 있다.
예를 들어 2차원 벡터를 1차원 공간에 투영한다고 해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
plt.ylim(-2,3)
plt.xlim(-2,3)
black = {'facecolor' : 'black'}
blue = {'facecolor' : 'blue'}
plt.annotate('', xy=[1,2], xytext=[0,0], arrowprops=black)
plt.text(0.5, 1.5, 'a')
plt.scatter(1,2, 100,'r')
plt.hlines(0, xmin=-2, xmax=3)
plt.annotate('', xy=[1,0], xytext=[0,0], arrowprops=blue)
plt.text(0.5, -0.3, 'b')
plt.scatter(1,0, 100,'r')
plt.vlines(1, ymin=0, ymax=2, ls=':', colors='r')
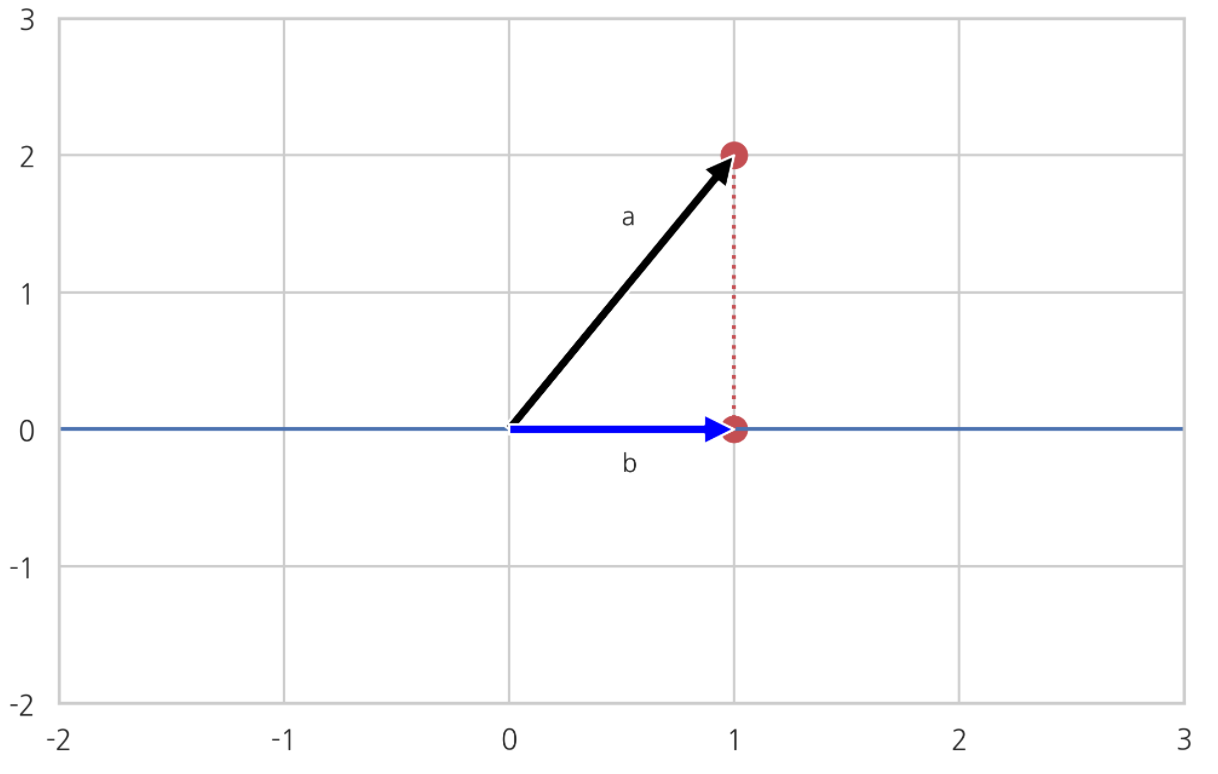
검은색 벡터 a 가 2차원 벡터다. 파란색 벡터 b가 2차원벡터 a를 1차원 공간에 투영한 투영성분 b다. 벡터 a의 나머지 성분은 붉은 점선 자리에 해당하는 직교벡터일 것이다.
곧, 파란색 벡터 b는 벡터 a 점과 수직이다. (a,b 둘 사이 거리가 수직 거리다)
한편, 파란색 선인 1차원 공간상에 무수히 많은 점들이 있을 것이다. 수많은 점(벡터) 중에서 벡터 b는 벡터 a와 가장 비슷한 벡터라고 볼 수 있다.
a,b 사이 유클리드거리를 통해 위 사실을 알 수 있다.
파란색 직선(저차원 공간) 상의 모든 점들은 벡터 a와의 코사인 유사도가 모두 같다.
코사인 유사도 관점에서, 직선 상의 모든 벡터들은 ‘다 똑같은 정도로 비슷하다’.
따라서 코사인 유사도만 가지고는 저차원 공간 상의 벡터 중 어떤 벡터가 벡터 a와 가장 비슷한지 알 수 없다.
벡터는 크기와 방향을 가지고 있었다. 두 벡터가 이루는 방향만 고려했을 때, 직선 위 모든 점들은 벡터 a와 똑같은 정도로 비슷했다. 방향만으로는 벡터 유사도 비교가 불가능하다.
그러면 벡터 크기도 방향과 함께 고려해서 벡터 간 유사도를 비교해보자. 유클리드거리를 이용할 수 있다. 유클리드거리는 벡터가 가리키는 점과 점 사이 거리로, 이 거리는 비교하는 두 벡터의 크기와 방향 모두를 감안한 값이다.
1
2
3
4
5
6
7
8
9
10
11
xx = np.arange(0,2+0.005, 0.005)
def test(b) :
return np.sqrt(5+(b**2)-2*np.sqrt(5)*b*(np.sqrt(5)/5))
tr = [test(b) for b in xx]
plt.plot(xx, tr)
plt.xlim(0,2)
plt.xlabel('벡터 b 길이')
plt.suptitle('고차원 벡터 a와 저차원 투영벡터 a_b 사이 유클리드 거리', y=1.03)
plt.title(': 고차원 벡터 a와 수직인 지점 벡터 a_b에서 유클리드 거리가 가장 작아졌다')
plt.show()

그래프를 그려보니 벡터 a의 저차원 투영벡터인 벡터 b(a_b) 에서 유클리드거리가 가장 작았다. 이를 통해 고차원벡터의 저차원 투영성분이 저차원공간의 벡터 중 원래 벡터와 가장 비슷한 벡터임을 알 수 있었다.
또, 점과 점 사이 수직거리가 두 점 사이 거리 중 가장 최단거리임을 알 수 있었다.
- 이처럼 유클리드 거리가 유용하긴 하지만, 위에 예시에 들었던 전제들 없이(예:벡터방향 모두 동일) 유클리드 거리만 가지고는 두 벡터 유사도 제대로 비교할 수 없다.
정규직교
- n개 벡터가 있는데, 이것들이 모두 단위벡터이고 서로 직교(벡터 간 내적이 0) 하면 ‘정규직교’라고 한다.
$\lVert v_{i} \rVert = 1$
$v_{i}^{T}v_{i} = 1$
$v_{i}^{T} v_{j} = 0 (i \ne j)$
코사인 유사도
$\cos{\theta} = \frac{a^{T}b}{\lVert a \rVert \lVert b \rVert}$
- 두 벡터가 비슷한 정도
두 벡터가 담고 있는 데이터가 얼마나 비슷한지 비교할 수 있다.
벡터의 길이는 상관없고, 벡터 방향만으로 두 벡터가 얼마나 비슷한지 판단할 수 있다.
두 벡터 방향이 비슷하면 코사인 유사도가 크다. 두 벡터가 비슷하다. 두 벡터가 담고 있는 데이터가 비슷하다.
두 벡터 방향이 다를 수록 코사인 유사도가 작아진다. 두 벡터가 다르다. 두 벡터가 담고 있는 데이터도 별로 유사하지 않다.
코사인 유사도 최댓값은 1이다. 두 벡터 방향이 같을 때 코사인 유사도 값이 1이다. 이때 코사인 유사도 관점에서 두 벡터는 ‘매우 비슷하다’
방향이 같은데 벡터 길이도 같다면, 두 벡터는 완전히 같은 벡터일 것이다.
벡터 내적으로 코사인 유사도 계산할 수 있다
벡터 내적은 다음과 같았다.
$a^{T}b = \lVert a \rVert \lVert b \rVert \cos{\theta}$
여러 벡터들을 가지고 쌍을 지어서 유사도를 비교할건데, 내적 식에서 $\lVert a \rVert \lVert b \rVert$ 이 부분이 다 비슷하다면 내적값은 결국 코사인 유사도 값일 것이다.
여기서 다음 사실을 알 수 있었다.
만약 두 벡터 길이가 다르면,
- 코사인 유사도 구해서 두 벡터가 비슷한 지 알 수 있다.
예)
벡터 내적만 가지고 코사인 유사도를 구하고, 두 벡터 사이 유사도를 계산해보자.
사이킷런 패키지 데이터셋 중에 숫자 이미지 데이터셋을 가져와서, 두 이미지가 비슷한지 안 비슷한지를 벡터 내적으로 구해보자.
벡터 내적만 가지고 두 벡터가 비슷한지, 안 비슷한지 보려면 벡터들의 길이가 다 비슷비슷해야 한다. 그래야 내적값이 곧 코사인 유사도 값이 될 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.datasets import load_digits
import matplotlib.gridspec as gridspec
digits = load_digits().images
digits_images = [digits[i] for i in np.arange(1797)]
norms = []
for i in np.arange(1797) :
v = digits[i].reshape(64,1)
norms.append(np.linalg.norm(v))
plt.stem(norms)

데이터셋에 있는 숫자 이미지 데이터 1797개를 모두 가져왔다. 그리고 이들을 모두 벡터로 변환시킨 후 , 각각의 놈 값들을 구해서 stem 플롯으로 나타냈다. 플롯이 균등분포 형태로, 모든 이미지의 놈(벡터 길이) 값이 대체로 비슷비슷함을 볼 수 있었다.
이제 그러면 벡터의 내적을 이용해서 코사인유사도를 구하고, 두 벡터가 비슷한지 알아보자.
1
2
3
4
v1 = digits[0].reshape(64,1)
v2 = digits[10].reshape(64,1)
v3 = digits[1].reshape(64,1)
v4 = digits[11].reshape(64,1)
숫자 이미지 4개를 골랐다. 모두 벡터로 변환시켰다.
어떤 이미지가 같은 종류 이미지고, 어떤 이미지가 다른 종류 이미지일까?
1
2
3
print((v1.T@v2)[0][0], (v3.T@v4)[0][0])
print((v1.T@v4)[0][0], (v1.T@v3)[0][0])
print((v2.T@v3)[0][0], (v2.T@v4)[0][0])
3064.0 3661.0
1883.0 1866.0
2421.0 2479.0
벡터들 간 내적값을 구해보니 v1과 v2 벡터, 그리고 v3와 v4 벡터가 내적값이 높게 나왔다. 나머지 조합에 대해서는 위에서 볼 수 있듯 내적값이 작게 나왔다.
이 결과를 놓고 보면 ‘v1과 v2’, ‘v3와 v4’가 같은 이미지겠거니 하고 추측할 수 있다. 벡터가 담고 있는 데이터가 유사하다는 뜻이다.
코사인 유사도도 구해보자.
1
2
3
4
5
6
7
8
9
10
11
# 코사인유사도 함수
def calc_cos(a,b) :
return (a.T@b)/(np.linalg.norm(a)*np.linalg.norm(b))
print(calc_cos(v1, v2)[0][0])
print(calc_cos(v3, v4)[0][0])
print(calc_cos(v1, v3)[0][0])
print(calc_cos(v1, v4)[0][0])
print(calc_cos(v2, v3)[0][0])
print(calc_cos(v2, v4)[0][0])
0.9191053370251786
0.8558850606827169
0.5191023426414686
0.5154497249105311
0.6202275328139769
0.6249243129435831
코사인 유사도 값들을 구해도 내적을 통해 내린 결론과 같은 결론 내릴 수 있었다. v1과 v2 벡터는 코사인 유사도가 1에 가까웠고, v3와 v4도 그에 버금가게 나왔다.
한편 나머지 벡터 조합에 대해서는 코사인 유사도 값들이 상대적으로 낮게 나왔다.
실제로 벡터를 다시 이미지로 변환시켜 출력해보면 v1과 v2가 같은 이미지였고, v3와 v4가 같은 이미지가 나왔다.
이를 통해 벡터들 길이가 비슷할 때, 내적을 이용하면 벡터 간의 유사도를 비교할 수 있음을 알 수 있었다.
벡터의 분해와 성분
- 벡터를 다른 두 벡터의 합으로 분리시키는 것을 ‘분해’라고 한다.
- 벡터를 분해시켜 나온 두 벡터를 각각 원래 벡터의 ‘성분’ 이라고 한다.
벡터의 투영성분과 직교성분
- 어떤 벡터 a를 다른 벡터 b에 평행하는 선분 하나와 벡터 b에 직교하는 성분 하나로 분해할 수 있다. 이때 전자를 ‘투영성분’, 후자를 ‘직교성분’ 이라고 한다.
투영성분 : $a^{\Vert{b}}$
직교성분 : $a^{\perp{b}}$
투영성분의 길이 : $\lVert a^{\Vert{b}} \rVert = a^{T}\frac{b}{\lVert b \rVert}$
투영성분벡터 : $a^{\Vert{b}} = a^{T}\frac{b}{\lVert b \rVert} \frac{b}{\lVert b \rVert}$
직교성분벡터 : $a^{\perp{b}} = a-a^{\Vert{b}}$
1
2
3
4
5
6
7
8
9
10
11
12
red = {'facecolor' : 'red'}
plt.xlim(-1,3)
plt.ylim(-1,3)
plt.annotate('', xy=[1,2], xytext=[0,0], arrowprops=black)
plt.annotate('', xy=[2,0], xytext=[0,0], arrowprops=blue)
plt.annotate('', xy=[1,0], xytext=[0,0], arrowprops=red)
plt.annotate('', xy=[0,2], xytext=[0,0], arrowprops=red)
plt.text(-0.6, 1.5, '직교성분 $a^{\Vert b}$')
plt.text(0.5, -0.3, '투영성분 $a^{\perp b}$')
plt.title('벡터 $b=[2,0]$ 에 대한 벡터 $a=[1,2]$의 투영성분과 직교성분')
plt.show()

메모)
방정식의 진짜 의미가 뭘까?
1 식 그 자체?
2 근?
방정식 = 함수 관계
방정식 = ‘관계’를 표시한 것에 불과하다.
$\Rightarrow$ 특정한 근 들의 관계를 나타낸 것이 ‘방정식’이다.
$\Rightarrow$ 방정식의 진짜 주인공은 특정한 관계를 갖는 근들 이다.
$\Rightarrow$ 수식은 근들의 관계를 나타낸 하나의 기호이자 상징에 불과하다.
