글 원본 : https://blog.naver.com/tigerkey10/222290281095
이 글은 내가 지킬 블로그를 만들기 전,
네이버 블로그에 공부 내용을 기록할 때 학습하고 복습하면서 기록했던 글을 옮겨온 것이다.
네이버 블로그에서 글을 옮겨와 지킬 블로그에도 기록해둔다.
모든 공부 과정을 기록으로 남겨 치열했던 시간들을 기록으로 남기고,
미래에 전달해 스스로 동기부여할 것이다. 또한 반복해서 학습. 복습하는 과정에서
어떤 개념에 대한 내 이해가 어떻게 변화.발전 했는지 관찰함으로써 스스로의 학습 정도를 돌아보는 거울로 삼고자 한다.
*부산대학교 오세민 교수님의 ‘데이터사이언스 입문’수업을 듣고,
교수님께서 제시하신 예제를 스스로 혼자 학습하고,
복습하면서 도출한 결론을 정리하였습니다*
미국 퀴즈쇼에서 진행했다는 유명한 몬티 홀 문제를 풀어보자.
이 문제는 베이즈 정리를 이해한다면 쉽게 풀 수 있는 확률 문제이다.
몬티 홀 퀴즈 쇼 규칙은 다음과 같다.
-
참가자는 3개의 문 중에서 하나를 선택한다.
-
문 뒤에는 염소 또는 자동차가 있다.
-
문 뒤에는 {염소,염소,자동차} 이런 식으로 상품이 있다.
-
만약 자동차를 선택하면 참가자는 자동차를 받아갈 수 있다.
-
참가자가 첫 선택을 내리면 사회자는 참가자가 선택하지 않은 문 중에서 무조건 염소를 보여준다.
-
참가자에게는 최종 결정에서, 첫 선택을 바꿔서 다른 문을 선택할지, 그대로 선택을 유지할 지 결정할 수 있다.
베이즈 정리
이 문제를 푸는 핵심은 ‘자동차 당첨되려면 바꾸는 행위가 유리한가? 선택을 유지하는 게 유리한가?’에 대답하는 것이다.
몬티홀 퀴즈에서 일어나는 각 사건들은 베이즈 정리를 이용해서 정의할 수 있다. 특정 사전확률이 사회자의 행위가 반영된 사후확률로
바뀔 것이고, 이 사건들을 종합해서 생각할 때, 바꾸는 게 당첨확률이 높은가? 유지하는 게 유리한가? 답할 수 있다.
단순화된 베이즈 정리 식은 다음과 같다.
$P(A\vert B) = \frac{P(B\vert A)*P(A)}{P(B)}$
용어
-
$P(A)$ : 사전확률
-
$P(B\vert A)$ : 가능도(해당 데이터가 특정 분포에 속해있을 확률)
-
$P(B)$ : 정규화 상수(분자 크기 조절 역할, 거의 영향력 없음)
-
$P(A\vert B)$ : 사후확률
몬티 홀 문제 [유지 vs 바꿈, 어떤 행위가 더 자동차 당첨 확률이 높은가?]
선택을 유지해서 자동차가 당첨될 확률부터 알아보자.
이 말의 전제는 내 첫 선택이 자동차를 골랐다는 것이다. 그러면 내가 자동차 당첨되는 사건을 A라고 하자. P(A)확률은 1/3이다.
| 사회자가 염소를 보여주는 사건을 B라고 하자. 내가 자동차를 처음에 고른 경우 사회자가 염소 보여주는 사건(가능도)의 확률 P(B | A)는 |
| 1/2이다(남은 염소 두 마리 중 하나 선택). 이를 이용해서 (P(B | A)*P(A)) / P(B)를 계산하면 P(A)의 사후확률을 알 수 있다. |
| P(A)의 사후확률 P(A | B)는 1/3이다. 이는 내가 선택을 유지해서 자동차 당첨될 확률이 1/3임을 의미한다. |
한편, 선택을 바꿔서 자동차가 당첨될 확률은 얼마인지 알아보자.
전제는 내 첫 선택이 염소였다는 것이다. 그래야 선택 바꿔서 특정확률로 자동차가 당첨될 것이다.
사건 A는 자동차 당첨되는 사건이다. P(A)는 1/3이다. 사회자가 염소 보여주는 사건은 B다. 내가 처음에 염소를 골랐다면,
| 사회자가 염소 보여주는 사건(가능도)의 확률 P(B | A)는 1이다(염소 고를 수 있는 선택지가 하나 뿐). 이를 이용해서 (P(B | A)*P(A)) / P(B)를 |
| 계산하면, P(A) 사후확률을 알 수 있다. 사후확률 P(A | B)는 2/3이다. 이는 사회자가 염소를 보여줌으로 해서, 자동차 당첨 확률이 바뀜을 |
| 말한다. 처음 사전확률이 1/3이었는데(P(A)) 사회자가 염소를 보여주는 행위(P(B | A))에 영향받아 자동차 당첨될 확률 P(A | B)가 2/3이 된 것이다. |
곧 처음에 내가 염소를 고르고 –> 사회자가 염소를 보여주고 –> 내가 선택지를 바꾸면 2/3 확률로 자동차가 당첨된다는 의미다.
선택을 유지해서 자동차가 당첨되는 경우의 확률값은 1/3이고, 선택을 바꿔서 자동차가 당첨되는 경우의 확률값은 2/3 이다.
선택을 바꾸는 경우의 자동차 당첨되는 확률값이 2/3으로 더 높기 때문에, 선택을 바꾸는 행위가 자동차 당첨에 더 유리하다고 말 할 수 있다.
선택지 바꿔서 자동차 당첨되는 경우의 통계적 확률을 직접 알아보자
선택지를 바꿔서 자동차 당첨되는 경우의 확률이 정말로 2/3일까? 직접 무수히 시행을 반복해서, 이 경우의 통계적 확률값을 구해보자.
#몬티 홀 문제
#1. 자동차,염소,염소가 랜덤으로 뽑히는 문을 3개 만들자.
import random
from random import randint
car = 1
goat = 0
door = [goat]*3
door[randint(0,2)] = car
door
코드는 위와 같다. 자동차를 1, 염소를 0으로 정의하고, 염소2마리와 자동차 1대가 랜덤으로 배치된 문을 만들었다.
#2. 내가 문 아무거나 하나 선택했다.
my_choice = randint(0,2) #내가 선택한 문 번호
mc_range = []
for i in range(0,3) :
if i != my_choice and door[i] != car :
mc_range.append(i) #mc가 선택할 수 있는 문 번호
if len(mc_range) == 2 :
mc_choice = mc_range[randint(0,1)]
elif len(mc_range) == 1 :
mc_choice = mc_range[0] #mc_choice = mc가 선택한 문 번호
그리고 내가 문을 하나 선택하고, 내 선택에 영향받은 MC가 문을 선택하는 사건들을 코드로 구현했다.
#선택 바꾸기
last = []
for a in range(0,3) :
if a != my_choice and a != mc_choice :
last.append(a)
last_choice = last[0]
#확률 계산하기
```python
door[last_choice] == car
나는 내가 선택을 바꾸어서 자동차가 당첨되는 경우의 통계적 확률을 알아보는 게 목적이다.
따라서 선택을 바꾼 사건을 코드로 구현했다.
코드 마지막 door[last_choice ] == car가 True이면 내가 선택을 바꿔서 자동차가 당첨되었음을,
False이면 선택 바꿔도 당첨되지 못했음을 의미한다. 여기까지는 ‘선택을 바꾸는’ 1회 시행의 결과를 코드로 표현한 것이다.
def monte(no) :
n=0
for c in range(no) :
car = 1
goat = 0
door = [goat]*3
door[randint(0,2)] = car
my_choice = randint(0,2) #내가 선택한 문 번호
mc_range = []
for i in range(0,3) :
if i != my_choice and door[i] != car :
mc_range.append(i) #mc가 선택할 수 있는 문 번호
if len(mc_range) == 2 :
mc_choice = mc_range[randint(0,1)]
elif len(mc_range) == 1 :
mc_choice = mc_range[0] #mc_choice = mc가 선택한 문 번호
last = []
for a in range(0,3) :
if a != my_choice and a != mc_choice :
last.append(a)
last_choice = last[0] #내가 마지막으로 선택한 문 번호
result = door[last_choice] == car
if result == True :
n += 1
return (round(n/no,5))
no = 1000000
monte(no)
이제 시행을 무수히 많이 반복할 것이다. 통계적 확률이란 시행을 무수히 많이 반복할 때, 시행 횟수에 상관 없이 특정 사건이 발생하는
확률을 의미한다. 위 코드로 통계적 확률값을 구할 것이다.
no변수에 1000000이라는 시행 횟수를 지정해주고, monte(no) 함수를 실행했다.
결과값은 몬티 홀 퀴즈쇼를 1000000번 반복할 때, 선택지 바꿔서 자동차 당첨되는 사건들의 통계적 확률값을 의미한다.
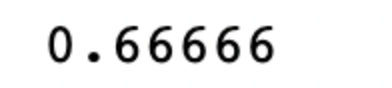
2/3은 0.66666이다. monte(no) 함수를 실행해보니 통계적 확률값이 0.666으로, 2/3과 일치하는 것을 볼 수 있었다.
선택지를 바꾸는 경우, 자동차가 당첨될 확률(통계적 확률)이 2/3임을 코드를 통해 실제로 입증할 수 있었다.
