대표본 일 때 모수 $\mu$ 구간추정
표본 갯수 n > 25 일 때.
모수 $\mu$ 에 대한 구간추정.
중심극한정리에 따라 표본들 평균 $\bar{X}$ 분포는 n이 충분히 클 때. 모분포에 상관없이, 근사적으로 기댓값 $\mu$, 표준편차 $\frac{\sigma}{\sqrt{n}}$ 인 정규분포 따른다.
$n > 25$ 이면 대표본이므로, 충분히 크다고 본다.
$\Rightarrow$ $n > 25$ 이면 $\bar{X}$ 분포는 근사적으로 정규분포 따른다.
이 $\bar{X}$ 를 표준화 시키면 그 표준화 된 것의 분포는 근사적으로 표준정규분포 $N(0,1)$ 을 따른다.
$\Rightarrow$ 어떤 구간의 면적을 자유롭게 구할 수 있게 된다.
이 표준정규분포 $N(0,1)$ 에서 확률분포함수와 X 축 사이 면적이 0.95 가 되는 구간이 모수 $\mu$ 의 95% 신뢰구간이 된다.
$P(-Z_{\alpha/2} \leq \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}} \leq Z_{\alpha/2}) \simeq 0.95$
$\pm Z = \pm 1.96$
식을 $\mu$ 를 중심으로 고친다.
$P(\bar{X}-1.96\frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X}+1.96\frac{\sigma}{\sqrt{n}}) \simeq 0.95$
위 구간이 모수 $\mu$ 에 대한 95% 신뢰구간이자 구간추정 결과가 된다.
- ‘95% 신뢰구간’의 의미는 위 구간을 100번 구했을 때, 95번은 이 구간이 모수 $\mu$ 를 포함한다는 의미다. 곧, 구간추정 방법의 정확도를 의미한다.
- 위 구간은 엄밀히 말해 모수 $\mu$ 에 대한 95% ‘근사적’ 신뢰구간 이다.
대표본. 기댓값 모수 $\mu$ 신뢰구간 구할 때. 모 표준편차 $\sigma$ 를 아는 경우
- 신뢰구간 식에 $\sigma$ 를 넣어서 구하면 된다.
만약 위 식에서 $\sigma = 3$ 이면,
$P(\bar{X}-1.96\frac{3}{\sqrt{n}} \leq \mu \leq \bar{X}+1.96\frac{3}{\sqrt{n}}) \simeq 0.95$ 이렇게 된다.
대표본. 기댓값 모수 $\mu$ 신뢰구간 구할 때. 모 표준편차 $\sigma$ 를 모르는 경우
- 신뢰구간 식에 $\sigma$ 대신 표본표준편차 $s$ 를 넣어도 상관 없다. (대표본 일 때 만)
$P(\bar{X}-1.96\frac{s}{\sqrt{n}} \leq \mu \leq \bar{X}+1.96\frac{s}{\sqrt{n}}) \simeq 0.95$
모수 $\mu$ 구간추정 응용 : 모비율 p 구간추정
만약 표본들이 베르누이 분포에서 나온 표본들이고, 표본 수 $n$ 이 매우 크면서, 모비율 $p$ 가 $0$과 $1$ 사이 적당한 값 인 경우. 모비율 $p$ 구간추정
- $np > 15, n(1-p) > 15$
모비율 $p$ 는 베르누이 분포 표본들의 평균과 같다.
$p = \frac{0,1로 이루어진 표본 총합 = 1 개수}{총 표본 수}$ 이기 때문이다.
따라서 모비율 $p$ 구간추정도 위에서 살펴본 모수 $\mu$ 구간추정과 같은 방식으로 할 수 있다.
$\Rightarrow$ 베르누이 분포의 실현된 표본들 총합을 $X$ 라고 하자.
이 $X$ 를 표본 총 갯수 $n$ 으로 나누면, $\frac{X}{n}$ 이 되고 이는 곧 모수 $p$ 에 대한 점 추정치(근삿값) 이자 검정통계량 값이다.
그리고 이 값은 베르누이 분포의 표본평균 값이다. 이 표본평균 값은 중심극한정리에 따라,
기댓값이 $p$, 분산이 $\frac{p(1-p)}{n}$ 인 정규분포 $N(p, \frac{p(1-p)}{n})$에 근사한다.
$\frac{X}{n}$ 을 표준화 시키면 $N(0,1)$ 표준정규분포를 근사적으로 따를 것이다.
$\Rightarrow \frac{\frac{X}{n} - p}{\sqrt{\frac{p(1-p)}{n}}} \sim N(0,1)$
이걸 이용해서 모비율 $p$ 에 대한 95% 근사적 신뢰구간을 구하면
$P(-Z_{\alpha/2} \leq \frac{\frac{X}{n} - p}{\sqrt{\frac{p(1-p)}{n}}} \leq +Z_{\alpha/2}) \simeq 0.95$
$\frac{X}{n}$ 의 표준편차 $\sqrt{\frac{p(1-p)}{n}}$ 에서 $p$ 값을 모른다.
앞에서 대표본을 가정했으므로, $p$를 $\hat{p} = \frac{X}{n}$ 로 대체할 수 있다.
최종으로 $p$ 95% 근사적 신뢰구간을 구하면 아래와 같다.
$P(\frac{X}{n} -Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \frac{X}{n}+Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}) \simeq 0.95$
소표본(표분 수 25 이하) & 모집단 정규성 가정 만족 할 때 모수 $\mu$ 구간추정
실현된 표본들이 정규분포에서 나온 표본들이면, 그 표본평균은 정확하게 정규분포 따른다.
$\bar{X} \sim N(\mu, \sigma^{2})$
대표본 일 때는 위 $\bar{X}$ 를 모르는 $\sigma$ 대신 표본표준편차 $s$ 써서 표준화 하면 $\bar{X}$ 가 표준정규분포 $N(0,1)$ 을 따랐다.
$\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}} \sim N(0,1)$
하지만 소표본 일 때는 $\sigma$ 대신 $s$ 를 써서 표준화 하면, $\bar{X}$ 가 자유도 n-1 인 student-T 분포를 따르게 된다.
$\Rightarrow$ $T = \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}} \sim T(n-1)$
- T 분포의 자유도가 $n-1$ 인 이유는 T 통계량 값의 자유도가 표본표준편차 $s$ 자유도 $n-1$ 에 의해 $n-1$ 이기 때문이다.
- $s = \frac{1}{n-1}\sum{(X_{i}-\bar{X})}^{2}$, $s$를 구하려면 $\bar{X}$ 를 알아야 하기 때문에 $s$의 자유도 $n-1$.
- 자유도 : $s$ 구하는 데 들어가는 (표본 갯수 $n$) $-$ ($s$ 구할 때 제약조건의 수)
T 분포의 주요 특징 3 가지
- 0에 대해 좌우대칭
- 자유도가 커질 수록 표준정규분포 $N(0,1)$ 에 가까이 간다
- 하지만 어떤 자유도에서도 t 분포 꼬리는 $N(0,1)$ 보다 두껍다.
$\frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}} \sim t(n-1)$
$P(-t_{\alpha/2} \leq \frac{\bar{X}-\mu}{\frac{s}{\sqrt{n}}} \leq +t_{\alpha/2}) = 0.95$
소표본, 정규분포에서 나온 표본들 일 때. 모수 $\mu$ 에 대한 95% 신뢰구간 :
$P(\bar{X}-t_{\alpha/2}\frac{s}{\sqrt{n}} \leq \mu \leq \bar{X} + t_{\alpha/2}\frac{s}{\sqrt{n}}) = 0.95$
정규분포에서 나온 표본들의 분산모수 $\sigma^{2}$ 추정
1. 분산모수 점 추정치
분산모수 $\sigma^{2}$ 의 점 추정치 : $s^{2}$
$s^{2} = \frac{1}{(n-1)} \sum{(X_{i} - \bar{X})}^{2}$
2. 분산모수 구간추정 (95% 신뢰구간)
위에서 $\sigma^{2}$ 에 대한 점 추정치는 $s^{2}$ 이었다.
이 $s^{2}$ 이 이루는 분포에서 면적이 95% 되는 구간 찾아야 한다.
확률값 구하기 쉽게 $s^{2}$ 를 $W$ 통계량으로 표준화 시키자.
$W = \frac{\sum{(X_{i} - \bar{X})^{2}}}{\sigma^{2}} = \frac{(n-1)s^{2}}{\sigma^{2}}$
이 $W$ 통계량은 카이제곱분포를 따른다.
이 $W$ 통계량은 $\bar{X}$ 를 알아야 구할 수 있다(제약조건). 따라서 자유도가 $n-1$ 이다.
$\Rightarrow$ $s^{2}$ 표준화시킨 $W$ 통계량은 자유도가 $n-1$ 인 카이제곱분포 따른다.
$W \sim \chi^{2}(n-1)$
카이제곱 분포에서 특정 점 오른쪽 면적이 $\alpha$ 이면, 그 점을 $\chi^{2}_{\alpha}$ 로 칭한다.
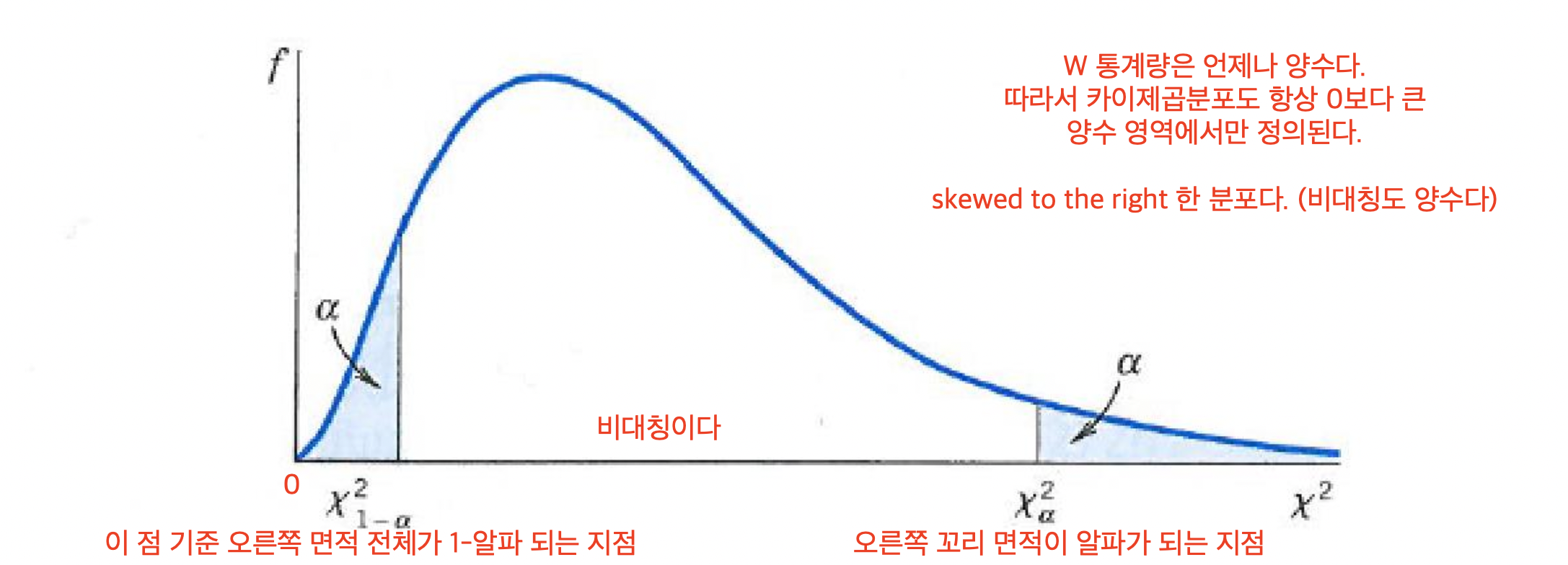
[이미지 출처: 부산대학교 통계학과 김충락 교수님의 R을 이용한 통계학개론_05_통계적 추론_2.pdf]
$ P(\chi_{1-\alpha}^{2} \leq \frac{(n-1)s^{2}}{\sigma^{2}} \leq \chi_{\alpha}^{2}) = 1-\alpha $
분산모수 $\sigma^{2}$ 에 대한 $100(1-\alpha)%$ 신뢰구간
$P(\frac{(n-1)s^{2}}{\chi_{\alpha/2}^{2}} \leq \sigma^{2} \leq \frac{(n-1)s^{2}}{\chi_{1-\frac{\alpha}{2}}^{2}}) = 1-\alpha$
표준편차 모수 $\sigma$ 에 대한 $100(1-\alpha)%$ 신뢰구간
$P(s\sqrt{\frac{(n-1)}{\chi_{\alpha/2}^{2}}} \leq \sigma \leq s\sqrt{\frac{(n-1)}{\chi_{1-\frac{\alpha}{2}}^{2}}}) = 1 - \alpha$
